فرهنگستان زبان و ادب
دانشنامه عمومی
گراف (ریاضی). گِراف یا نِگار در ریاضیات دست کم دارای دو معنی می باشد. در ریاضیات پایه گراف اشاره به نمودار تابع دارد، و در اصطلاح ریاضی دانان، گراف مجموعه ای از نقاط و خطوط به هم پیوسته است.
در واقع گراف مدلی ریاضی برای یک مجموعه گسسته است که اعضایش به گونه ای با هم پیوند دارند. اعضای این مجموعه می توانند چند انسان باشند و ارتباط میان آن ها دست دادن با یکدیگر باشد. اعضا می توانند اتم ها در یک مولکول باشند و ارتباطشان پیوندهای شیمیایی باشد یا این که اعضا می توانند بخش های گوناگون یک زمین و ارتباط میانشان، پل هایی باشد که آن ها را به هم می پیوندند ( همانند مسئله کونیگسبرگ ) . [ ۱]
نظریه گراف یکی از موضوع های مهم در ریاضیات گسسته است که به شناخت گراف ها و مدل بندی مسایل با آن ها می پردازد. لئونارد اویلر در سال ۱۷۳۶ با حل مسئله پل های کونیگسبرگ نظریهٔ گراف ها را بنیان گذاشت. اما جیمز جوزف سیلوستر نخستین کسی بود که در سال ۱۸۷۸ این مدل های ریاضی را گراف نامید. [ ۲]
گراف ساده: یک گراف از مجموعه ای غیر خالی از اشیاء به نام رأس تشکیل شده، که آن را با V نشان می دهیم، و مجموعه ای شامل یال ها، که رأس ها را به هم وصل می کنند و با E نمایش می دهیم. یک چنین گرافی را با G = ( V , E ) نشان می دهیم. اگر یال y دو رأس v 1 و v 2 را به هم وصل کند می نویسیم y = { v 1 , v 2 } . [ ۳]
گراف جهت دار: منظور از گراف جهت دار گرافی است که یال ها در آن دارای جهت هستند. گراف جهت دار G زوج مرتب ( V, E ) است که V مجموعه ای ناتهی و اعضای E زوجهای مرتب از اعضای V هستند. همانند گرافهای ساده، به اعضایV، راسهای G و به اعضای E، یال های G می گوییم. همچنین به هر گراف جهت دار نموداری در صفحه نسبت می دهیم. به این صورت که به ازای هر راس G نقطه ای در صفحه در نظر می گیریم و به ازای هر یال مانند ( u, v ) کمانی بین u و v رسم می کنیم و روی این کمان فلشی از u به v می گذاریم.
گراف مخلوط: گرافی است که در آن ممکن است برخی یال ها جهت داشته باشند و برخی بدون جهت باشند. گراف مخلوط G، سه تایی مرتب G = ( V, E, A ) است که در آن V مجموعهٔ رئوس، E یال های بدون جهت و A یال های جهت دارمی باشند. گراف ساده و گراف جهت دار حالت خاصی از گراف جهت دار می باشند.
گراف وزن دار: گراف وزن دار، گرافی است که به هر یک از یال ها یا به هریک از راس های آن عددی نسبت داده شده است که وزن آن یال یا راس می باشد. وزن یال می تواند نشان دهندهٔ هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد. بعضی از نویسنده ها به گراف وزن دار گراف شبکه ای می گویند.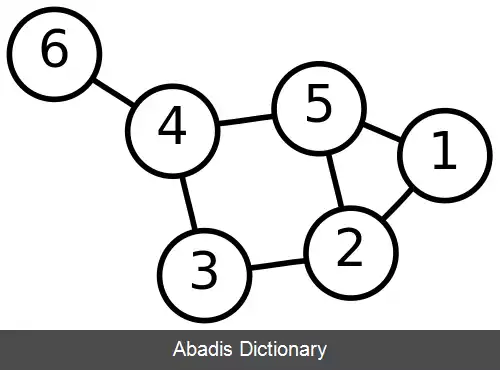
در واقع گراف مدلی ریاضی برای یک مجموعه گسسته است که اعضایش به گونه ای با هم پیوند دارند. اعضای این مجموعه می توانند چند انسان باشند و ارتباط میان آن ها دست دادن با یکدیگر باشد. اعضا می توانند اتم ها در یک مولکول باشند و ارتباطشان پیوندهای شیمیایی باشد یا این که اعضا می توانند بخش های گوناگون یک زمین و ارتباط میانشان، پل هایی باشد که آن ها را به هم می پیوندند ( همانند مسئله کونیگسبرگ ) . [ ۱]
نظریه گراف یکی از موضوع های مهم در ریاضیات گسسته است که به شناخت گراف ها و مدل بندی مسایل با آن ها می پردازد. لئونارد اویلر در سال ۱۷۳۶ با حل مسئله پل های کونیگسبرگ نظریهٔ گراف ها را بنیان گذاشت. اما جیمز جوزف سیلوستر نخستین کسی بود که در سال ۱۸۷۸ این مدل های ریاضی را گراف نامید. [ ۲]
گراف ساده: یک گراف از مجموعه ای غیر خالی از اشیاء به نام رأس تشکیل شده، که آن را با V نشان می دهیم، و مجموعه ای شامل یال ها، که رأس ها را به هم وصل می کنند و با E نمایش می دهیم. یک چنین گرافی را با G = ( V , E ) نشان می دهیم. اگر یال y دو رأس v 1 و v 2 را به هم وصل کند می نویسیم y = { v 1 , v 2 } . [ ۳]
گراف جهت دار: منظور از گراف جهت دار گرافی است که یال ها در آن دارای جهت هستند. گراف جهت دار G زوج مرتب ( V, E ) است که V مجموعه ای ناتهی و اعضای E زوجهای مرتب از اعضای V هستند. همانند گرافهای ساده، به اعضایV، راسهای G و به اعضای E، یال های G می گوییم. همچنین به هر گراف جهت دار نموداری در صفحه نسبت می دهیم. به این صورت که به ازای هر راس G نقطه ای در صفحه در نظر می گیریم و به ازای هر یال مانند ( u, v ) کمانی بین u و v رسم می کنیم و روی این کمان فلشی از u به v می گذاریم.
گراف مخلوط: گرافی است که در آن ممکن است برخی یال ها جهت داشته باشند و برخی بدون جهت باشند. گراف مخلوط G، سه تایی مرتب G = ( V, E, A ) است که در آن V مجموعهٔ رئوس، E یال های بدون جهت و A یال های جهت دارمی باشند. گراف ساده و گراف جهت دار حالت خاصی از گراف جهت دار می باشند.
گراف وزن دار: گراف وزن دار، گرافی است که به هر یک از یال ها یا به هریک از راس های آن عددی نسبت داده شده است که وزن آن یال یا راس می باشد. وزن یال می تواند نشان دهندهٔ هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد. بعضی از نویسنده ها به گراف وزن دار گراف شبکه ای می گویند.




wiki: گراف (ریاضی)
گراف (ساختار داده). یک گراف[ ۱] ( به انگلیسی: graph ) در علوم رایانه، داده ساختاری انتزاعی است که به صورت گراف جهت دار و بدون جهت پیاده سازی می شود و. هدفش به کارگیریِ مفهوم گراف از ریاضیات و به خصوص نظریه گراف است.
یک داده ساختار گراف اساساً از یک مجموعهٔ متناهیِ زوج های مرتب موسوم به یال شامل واحدهایی به نام رأس یا گره تشکیل می شود؛ همان طور که در ریاضیات به ازای یک یال ( u, v ) می گوییم که u به v می رود یا u و v مجاورند. همچنین می توان به هر یال یک گراف یک عدد نسبت داد که در این صورت گراف وزن دار به وجود می آید.
عملیات ابتدایی ارائه شده توسط یک ساختار داده گراف G معمولاً شامل:[ ۲]
• مجاورت ( G, x, y ) : امتحان اینکه آیا یک یال از رأس x به رأس y وجود دارد؛
• همسایه ها ( G, x ) :لیست تمام رأس ها را به طوری که یک یال از رأس x به رأس y وجود دارد؛
• درج راس ( G, x ) :راس x را در صورت عدم وجود اضافه می کند؛
• حذف راس ( G, x ) :راس x را در صورت وجود حذف می کند؛
• درج یال ( G, x, y ) : یک یال از رأس x به رأس y اضافه می کند؛
• حذف یال ( G, x, y ) : یال از رأس x به رأس y را در صورت وجود حذف می کند؛
• گرفتن ارزش راس ( G, x ) : مقدار مربوط به رأس x را برمی گرداند؛
• مقداردهی راس ( G, x, v ) :مقدار مربوط به رأس x را v قرار می دهد.
در گراف وزن دار دستورهای زیر نیز وجود دارد:
• گرفتن ارزش یال ( G, x, y ) :مقدار مربوط به یال گذرنده از ( x, y ) را بازمی گرداند؛
• مقدار دهی یال ( G, x, y, v ) : مقدار مربوط به لبه ( x, y ) را به v تنظیم می کند.
ساختار داده های مختلفی برای نمایش گراف ها در عمل استفاده می شود:
راس ها به عنوان سوابق یا اشیا ذخیره می شوند و هر رأس لیستی از رأس های مجاور را ذخیره می کند. این ساختار داده ها اجازه ذخیره سازی داده های اضافی در رأس ها را می دهد. داده های اضافی را می توان ذخیره کرد اگر یال ها نیز به عنوان اشیا ذخیره شوند، در این صورت هر رأس یال های حادث بر خود را ذخیره می کند و هر یال رأس حاد خود را ذخیره می کند.
یک ماتریس دو بعدی، که در آن ردیف ها نشان دهنده رأس مبدأ و ستون ها نشان دهنده راس مقصد هستند. داده ها در یال ها و رأس ها باید در خارج از ماتریس ذخیره شوند. فقط هزینه یک یال می تواند بین هر جفت رأس ذخیره شود.
یک ماتریس بولی دو بعدی، که در آن ردیف ها نشان دهنده رأس ها و ستون هانشان دهنده یال ها هستند. ورودی ها نشان می دهند که آیا رأس یک ردیف به یال یک ستون متصل است یا خیر.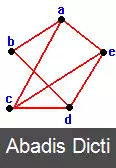
یک داده ساختار گراف اساساً از یک مجموعهٔ متناهیِ زوج های مرتب موسوم به یال شامل واحدهایی به نام رأس یا گره تشکیل می شود؛ همان طور که در ریاضیات به ازای یک یال ( u, v ) می گوییم که u به v می رود یا u و v مجاورند. همچنین می توان به هر یال یک گراف یک عدد نسبت داد که در این صورت گراف وزن دار به وجود می آید.
عملیات ابتدایی ارائه شده توسط یک ساختار داده گراف G معمولاً شامل:[ ۲]
• مجاورت ( G, x, y ) : امتحان اینکه آیا یک یال از رأس x به رأس y وجود دارد؛
• همسایه ها ( G, x ) :لیست تمام رأس ها را به طوری که یک یال از رأس x به رأس y وجود دارد؛
• درج راس ( G, x ) :راس x را در صورت عدم وجود اضافه می کند؛
• حذف راس ( G, x ) :راس x را در صورت وجود حذف می کند؛
• درج یال ( G, x, y ) : یک یال از رأس x به رأس y اضافه می کند؛
• حذف یال ( G, x, y ) : یال از رأس x به رأس y را در صورت وجود حذف می کند؛
• گرفتن ارزش راس ( G, x ) : مقدار مربوط به رأس x را برمی گرداند؛
• مقداردهی راس ( G, x, v ) :مقدار مربوط به رأس x را v قرار می دهد.
در گراف وزن دار دستورهای زیر نیز وجود دارد:
• گرفتن ارزش یال ( G, x, y ) :مقدار مربوط به یال گذرنده از ( x, y ) را بازمی گرداند؛
• مقدار دهی یال ( G, x, y, v ) : مقدار مربوط به لبه ( x, y ) را به v تنظیم می کند.
ساختار داده های مختلفی برای نمایش گراف ها در عمل استفاده می شود:
راس ها به عنوان سوابق یا اشیا ذخیره می شوند و هر رأس لیستی از رأس های مجاور را ذخیره می کند. این ساختار داده ها اجازه ذخیره سازی داده های اضافی در رأس ها را می دهد. داده های اضافی را می توان ذخیره کرد اگر یال ها نیز به عنوان اشیا ذخیره شوند، در این صورت هر رأس یال های حادث بر خود را ذخیره می کند و هر یال رأس حاد خود را ذخیره می کند.
یک ماتریس دو بعدی، که در آن ردیف ها نشان دهنده رأس مبدأ و ستون ها نشان دهنده راس مقصد هستند. داده ها در یال ها و رأس ها باید در خارج از ماتریس ذخیره شوند. فقط هزینه یک یال می تواند بین هر جفت رأس ذخیره شود.
یک ماتریس بولی دو بعدی، که در آن ردیف ها نشان دهنده رأس ها و ستون هانشان دهنده یال ها هستند. ورودی ها نشان می دهند که آیا رأس یک ردیف به یال یک ستون متصل است یا خیر.

wiki: گراف (ساختار داده)
گراف (لقب اشرافی). گراف یا معادل مؤنث گرِفین ( آلمانی: Graf/Gräfin، مجاری/اسلواکی: gróf, کرواتی: grof ) لقب بلندپایهٔ اشرافی - موروثی رایج در امپراتوری فرانک بود. این عنوان اغلب به کنت نیز ترجمه می شود. مقام ویکنت پایین تر و مارکی از آن بالاتر است.
عنوان گراف در کشورهای آلمانی زبان رسمی یا محلی از جمله اتریش، آلمان، سوئیس، لوکزامبورگ، لیختن اشتاین، آلزاس، بالتیک و دیگر مناطق تحت تسلط هابسبورگ سابق استفاده می شود. [ ۱]
واژه های قدیمی آلمانی grafio و gravo برگرفته از گرافئوس ( grapheus ) بیزانسی باستان و یونانی گرافین ( γρᾰ́φειν ) به معنی نوشتن هستند. لاتین این واژه ( فرانسوی comte/comtesse، انگلیسی count/countess، ایتالیایی conte/contessa، اسپانیایی conde/condesa ) به معنای «همدم ( پادشاه ) » است. در اواخر دوران روم، از مقامات بلندپایه مالی امپراتوری به عنوان comelaritionum یا همدم خزانه یاد می شد.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعنوان گراف در کشورهای آلمانی زبان رسمی یا محلی از جمله اتریش، آلمان، سوئیس، لوکزامبورگ، لیختن اشتاین، آلزاس، بالتیک و دیگر مناطق تحت تسلط هابسبورگ سابق استفاده می شود. [ ۱]
واژه های قدیمی آلمانی grafio و gravo برگرفته از گرافئوس ( grapheus ) بیزانسی باستان و یونانی گرافین ( γρᾰ́φειν ) به معنی نوشتن هستند. لاتین این واژه ( فرانسوی comte/comtesse، انگلیسی count/countess، ایتالیایی conte/contessa، اسپانیایی conde/condesa ) به معنای «همدم ( پادشاه ) » است. در اواخر دوران روم، از مقامات بلندپایه مالی امپراتوری به عنوان comelaritionum یا همدم خزانه یاد می شد.

wiki: گراف (لقب اشرافی)
مترادف ها
گراف، گرافیک، طرح خطی، نمایش هندسی، نقشه هندسی، هجای کلمه، اشکال مختلف یک حرف
پیشنهاد کاربران
نمودار یا گراف گ و ها ( Graph of G & H یا
Graph of God and Holy Spirit ) یعنی نمایش گرافیکی حرکت خدا و روح مقدس از بهشت برین تا رجعت یا بازگشتشان به بهشت برین روی یک مسیر دایره ای شکل تحت عنوان دور مقدس خدائی یا دور عقلانی، روحی، ایده ای، مفهومی، فکری و منطقی محض هگلی ( ویلیام ) .
... [مشاهده متن کامل]
البته خدای حقیقی و واقعی بهمراه اجزاء کثیر یا فراوان زنده و غیر زنده و واحد بودن خمیرمایه ی ساختاری تثلیثی یا سه جنبه ای مادی - روانی - روحی کالبد، تن و یا بدن بیکران وی ( به زبان علمی : انرژی - جرم - خلاء به شکل اتم ها ) و نه خدای کلمه ای بنام God با تلفظ گاد به زبان انگلیسی یا زبان های دیگر با تلفظ های مختلف.
مسیر این حرکت یا سفر بسیار طولانی و دایره وار دنیوی، مقطعی، نزولی و صعودی ، پیوسته یا آنالوگ نمی باشد بلکه ناپیوسته یا دیجیتال یعنی وادی به وادی، منزل به منزل، پله به پله یا ایستگاه به ایستگاه در مدارات، مراتب یا درجات فراوان تکاملی بین دو حد دنیوی؛ یکی نهایت نقصان و امکان اخس در پائین ترین حالت نشئگی طبیعی و دیگری نهایت کمال و امکان اشرف دنیوی در بالاترین حالت نشئگی طبیعی قبل از وقع آخرین مهبانگ و بازگشت به همان نظام احسن و اشرف آفرینش سرمدی، مبدئی، معادی، ازلی و ابدی یا اولیه در نهایت کمال ایده آل خوبی و زیبایی، اعتدال و نظم و هماهنگی با کمیت و کیفیت بهشت و آنهم نه یکبار و صدبار و هزار و یکبار بلکه به تعداد کلیه ی حلقه های زنجیره دایره وار علت و معلول و یا به بیانی دیگر به تعداد همه ی کنگره های سلسله دایره وار دهّر ها، از طریق گردش دایره وار وقوع مهبانگ های هفتگانه بر اثر نوسانات خودکار و متوالی انبساط و انقباض در چهارچوب طرح مطلق آفرینش و بر اساس قوانین جاودانه و آئین نامه های اجرایی ثابت و پایدار و تغییر ناپذیر آن و نه از راه و به روشی دیگر .
Hamiltonian Icosian Game : بازی آیکوسیان همیلتونی!
Icosian از چهار کلمه ساخته شده ؛ I با تلفظ آی در زبان انگلیسی معادل ضمیر اول شخص مفرد در زبان فارسی یعنی من و co با دو معنا یکی مخفف کوه در زبان فارسی و دیگری چندتائی و si با تلفظ زی به معنای زندگی و an با تلفظ آن معادل ضمیر سوم شخص مفرد در زبان فارسی.
لذا آی یا من یعنی ویلیام رووان همیلتون و آن کوه از چندین زندگی دنیوی برخورداریم.
همیلتون ( هم ایلیِ تون یعنی هم سفر تون ) برای گم نمودن ردپا و ریشه های لفظی این واژه ی ترکیبی ( آیکوزیَن یا آیکوسیان ) بجای بکار بردن کلمه ی زیون ( Zion ) که در زبان فارسی قدیم و آرامی به معنای زندگان بوده، کلمه ی sian با تلفظ زیَن را مورد استفاده قرار داده و آنرا بهمراه گَیم یا بازی در میدان رقابت با بازی کابلای حکیمان و عارفان پیرو دین یهود بکار برده که بازی با حروف و اعداد میباشد و نه نمایش گرافیکی یا نموداری سفر.
تعداد راس ها یا گره ها، یال و کوپال ها یا خط های دایره وار پیوندی بین گره های همجوار یا همسایه یا تعداد برآمدگی ها و فرورفتگی های متناوب یا متوالی این سلسله ی کنگره ای یا دندانه دار و یا این جاده یا راه موجی شکل سینوسی یا کوسینوسی به روش علمی با یقین و اطمینان کامل یا صددرصد قابل محاسبه و تعیین میباشد و در قالب یک عدد بزرگ قابل بیان و نوشتن و نمایش و نگارش.
برای انجام چنین محاسبه ای به دو گاو شخمی و یکی دوتا یوغ سبک نجات و شفا و یک مرد جوانسال مانند ایسا و یا یک مرد پیر مانند همینگوی و دریای مدیترانه نیازی نداریم بلکه یکی دو تا دانش آموز زیرک و باهوش و یک ماشین حساب مناسب یا مهندسی، که بتوانند به کمک آن در قدم اول محاسباتی، عدد 10 بتوان 43 ثانیه را به سال شمسی ( و نه قمری ) تبدیل و سپس آنرا تقسیم بر 90 میلیارد سال نمایند و سپس آنرا روی یک برگ کاغذ بنویسند و پسوند بار یا دفعه را به آن بیفزایند. البته در هر دوری باید 630 میلیارد سال از طول زمانی دور قبل کاسته شود تا در پایان سفر 0 باقی بماند. یعنی 10 بتوان 43 ثانیه منهای X ضربدر 630 میلیارد سال و سپس محاسبه ی مجهول X که مساوی با حاصل همان تقسیم خواهد بود.
دانش آموزان زیرک و باهوش میدانند که برای انجام این محاسبه در ماشین حساب لزومی ندارد که پسوند های ثانیه و سال را تایپ نمایند بلکه فقط اعداد را.
Graph of God and Holy Spirit ) یعنی نمایش گرافیکی حرکت خدا و روح مقدس از بهشت برین تا رجعت یا بازگشتشان به بهشت برین روی یک مسیر دایره ای شکل تحت عنوان دور مقدس خدائی یا دور عقلانی، روحی، ایده ای، مفهومی، فکری و منطقی محض هگلی ( ویلیام ) .
... [مشاهده متن کامل]
البته خدای حقیقی و واقعی بهمراه اجزاء کثیر یا فراوان زنده و غیر زنده و واحد بودن خمیرمایه ی ساختاری تثلیثی یا سه جنبه ای مادی - روانی - روحی کالبد، تن و یا بدن بیکران وی ( به زبان علمی : انرژی - جرم - خلاء به شکل اتم ها ) و نه خدای کلمه ای بنام God با تلفظ گاد به زبان انگلیسی یا زبان های دیگر با تلفظ های مختلف.
مسیر این حرکت یا سفر بسیار طولانی و دایره وار دنیوی، مقطعی، نزولی و صعودی ، پیوسته یا آنالوگ نمی باشد بلکه ناپیوسته یا دیجیتال یعنی وادی به وادی، منزل به منزل، پله به پله یا ایستگاه به ایستگاه در مدارات، مراتب یا درجات فراوان تکاملی بین دو حد دنیوی؛ یکی نهایت نقصان و امکان اخس در پائین ترین حالت نشئگی طبیعی و دیگری نهایت کمال و امکان اشرف دنیوی در بالاترین حالت نشئگی طبیعی قبل از وقع آخرین مهبانگ و بازگشت به همان نظام احسن و اشرف آفرینش سرمدی، مبدئی، معادی، ازلی و ابدی یا اولیه در نهایت کمال ایده آل خوبی و زیبایی، اعتدال و نظم و هماهنگی با کمیت و کیفیت بهشت و آنهم نه یکبار و صدبار و هزار و یکبار بلکه به تعداد کلیه ی حلقه های زنجیره دایره وار علت و معلول و یا به بیانی دیگر به تعداد همه ی کنگره های سلسله دایره وار دهّر ها، از طریق گردش دایره وار وقوع مهبانگ های هفتگانه بر اثر نوسانات خودکار و متوالی انبساط و انقباض در چهارچوب طرح مطلق آفرینش و بر اساس قوانین جاودانه و آئین نامه های اجرایی ثابت و پایدار و تغییر ناپذیر آن و نه از راه و به روشی دیگر .
Hamiltonian Icosian Game : بازی آیکوسیان همیلتونی!
Icosian از چهار کلمه ساخته شده ؛ I با تلفظ آی در زبان انگلیسی معادل ضمیر اول شخص مفرد در زبان فارسی یعنی من و co با دو معنا یکی مخفف کوه در زبان فارسی و دیگری چندتائی و si با تلفظ زی به معنای زندگی و an با تلفظ آن معادل ضمیر سوم شخص مفرد در زبان فارسی.
لذا آی یا من یعنی ویلیام رووان همیلتون و آن کوه از چندین زندگی دنیوی برخورداریم.
همیلتون ( هم ایلیِ تون یعنی هم سفر تون ) برای گم نمودن ردپا و ریشه های لفظی این واژه ی ترکیبی ( آیکوزیَن یا آیکوسیان ) بجای بکار بردن کلمه ی زیون ( Zion ) که در زبان فارسی قدیم و آرامی به معنای زندگان بوده، کلمه ی sian با تلفظ زیَن را مورد استفاده قرار داده و آنرا بهمراه گَیم یا بازی در میدان رقابت با بازی کابلای حکیمان و عارفان پیرو دین یهود بکار برده که بازی با حروف و اعداد میباشد و نه نمایش گرافیکی یا نموداری سفر.
تعداد راس ها یا گره ها، یال و کوپال ها یا خط های دایره وار پیوندی بین گره های همجوار یا همسایه یا تعداد برآمدگی ها و فرورفتگی های متناوب یا متوالی این سلسله ی کنگره ای یا دندانه دار و یا این جاده یا راه موجی شکل سینوسی یا کوسینوسی به روش علمی با یقین و اطمینان کامل یا صددرصد قابل محاسبه و تعیین میباشد و در قالب یک عدد بزرگ قابل بیان و نوشتن و نمایش و نگارش.
برای انجام چنین محاسبه ای به دو گاو شخمی و یکی دوتا یوغ سبک نجات و شفا و یک مرد جوانسال مانند ایسا و یا یک مرد پیر مانند همینگوی و دریای مدیترانه نیازی نداریم بلکه یکی دو تا دانش آموز زیرک و باهوش و یک ماشین حساب مناسب یا مهندسی، که بتوانند به کمک آن در قدم اول محاسباتی، عدد 10 بتوان 43 ثانیه را به سال شمسی ( و نه قمری ) تبدیل و سپس آنرا تقسیم بر 90 میلیارد سال نمایند و سپس آنرا روی یک برگ کاغذ بنویسند و پسوند بار یا دفعه را به آن بیفزایند. البته در هر دوری باید 630 میلیارد سال از طول زمانی دور قبل کاسته شود تا در پایان سفر 0 باقی بماند. یعنی 10 بتوان 43 ثانیه منهای X ضربدر 630 میلیارد سال و سپس محاسبه ی مجهول X که مساوی با حاصل همان تقسیم خواهد بود.
دانش آموزان زیرک و باهوش میدانند که برای انجام این محاسبه در ماشین حساب لزومی ندارد که پسوند های ثانیه و سال را تایپ نمایند بلکه فقط اعداد را.
گِراف در ریاضیات دست کم دارای دو معنی می باشد. در ریاضیات پایه گراف اشاره به نمودار تابع دارد، و در اصطلاح ریاضی دانان گراف مجموعه ای از نقاط و خطوط به هم پیوسته است.
در واقع گراف مدلی ریاضی برای یک مجموعه گسسته است که اعضایش به گونه ای با هم پیوند دارند. اعضای این مجموعه می توانند چند انسان باشند و ارتباط میان آن ها دست دادن با یکدیگر باشد. اعضا می توانند اتم ها در یک مولکول باشند و ارتباطشان پیوندهای شیمیایی باشد یا این که اعضا می توانند بخش های گوناگون یک زمین و ارتباط میانشان، پل هایی باشد که آن ها را به هم می پیوندند ( همانند مسئله کونیگسبرگ ) .
... [مشاهده متن کامل]
نظریه گراف یکی از موضوع های مهم در ریاضیات گسسته است که به شناخت گراف ها و مدل بندی مسایل با آن ها می پردازد. لئونارد اویلر در سال ۱۷۳۶ با حل مسئله پل های کونیگسبرگ نظریهٔ گراف ها را بنیان گذاشت. اما جیمز جوزف سیلوستر نخستین کسی بود که در سال ۱۸۷۸ این مدل های ریاضی را گراف نامید.
در واقع گراف مدلی ریاضی برای یک مجموعه گسسته است که اعضایش به گونه ای با هم پیوند دارند. اعضای این مجموعه می توانند چند انسان باشند و ارتباط میان آن ها دست دادن با یکدیگر باشد. اعضا می توانند اتم ها در یک مولکول باشند و ارتباطشان پیوندهای شیمیایی باشد یا این که اعضا می توانند بخش های گوناگون یک زمین و ارتباط میانشان، پل هایی باشد که آن ها را به هم می پیوندند ( همانند مسئله کونیگسبرگ ) .
... [مشاهده متن کامل]
نظریه گراف یکی از موضوع های مهم در ریاضیات گسسته است که به شناخت گراف ها و مدل بندی مسایل با آن ها می پردازد. لئونارد اویلر در سال ۱۷۳۶ با حل مسئله پل های کونیگسبرگ نظریهٔ گراف ها را بنیان گذاشت. اما جیمز جوزف سیلوستر نخستین کسی بود که در سال ۱۸۷۸ این مدل های ریاضی را گراف نامید.
گراف ساده: یک گراف از مجموعه ای غیر خالی از اشیاء به نام رأس تشکیل شده، که آن را با {\displaystyle V}V نشان می دهیم، و مجموعه ای شامل یال ها، که رأس ها را به هم وصل می کنند و با {\displaystyle E}E نمایش می دهیم. یک چنین گرافی را با {\displaystyle G= ( V, E ) }G= ( V, E ) نشان می دهیم. اگر یال {\displaystyle y}y دو رأس {\displaystyle v_{1}}v_{1} و {\displaystyle v_{2}}v_{2} را به هم وصل کند می نویسیم {\displaystyle y=\lbrace v_{1}, v_{2}\rbrace }y=\lbrace v_{1}, v_{2}\rbrace . [۳]
... [مشاهده متن کامل]
گراف جهت دار: منظور از گراف جهت دار گرافی است که یال ها در آن دارای جهت هستند. گراف جهت دار G زوج مرتب ( V, E ) است که V مجموعه ای ناتهی و اعضای E زوجهای مرتب از اعضای V هستند. همانند گرافهای ساده، به اعضایV، راسهای G و به اعضای E، یال های G می گوییم. همچنین به هر گراف جهت دار نموداری در صفحه نسبت می دهیم. به این صورت که به ازای هر راس G نقطه ای در صفحه در نظر می گیریم و به ازای هر یال مانند ( u, v ) کمانی بین u و v رسم می کنیم و روی این کمان فلشی از u به v می گذاریم.
گراف مخلوط: گرافی است که در آن ممکن است برخی یال ها جهت داشته باشند و برخی بدون جهت باشند. گراف مخلوط G، سه تایی مرتب G = ( V, E, A ) است که در آن V مجموعه ی رئوس، E یال های بدون جهت و A یال های جهت دارمی باشند. گراف ساده و گراف جهت دار حالت خاصی از گراف جهت دار می باشند.
گراف وزن دار: گراف وزن دار، گرافی است که به هر یک از یال ها یا به هریک از راس های آن عددی نسبت داده شده است که وزن آن یال یا راس می باشد. وزن یال می تواند نشان دهنده هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد. بعضی از نویسنده ها به گراف وزن دار گراف شبکه ای می گویند.
قرارداد ها:
مرتبه و اندازۀ یک گراف: تعداد رأس های گراف G یعنی |V ( G ) | را مرتبهٔ آن گراف می گوییم و باp ( G ) نمایش می دهیم و تعداد یال های گراف یعنی |E ( G ) | را اندازهٔ گراف G می گوییم و با q ( G ) نمایش می دهیم. معمولاً برای راحتی کار به جای p ( G ) از p و به جای q ( G ) از q استفاده می کنیم.
درجۀ یک رأس: درجهٔ رأس v در گراف G برابر است با تعداد یال هایی از گراف G که به رأس v متصل اند و آن را با degG ( v ) یا به طور ساده تر با deg ( v ) یا d ( v ) نمایش می دهیم. اگر درجهٔ یک رأس فرد باشد آن را رأس فرد و اگر زوج باشد آن را رأس زوج می نامیم.
گراف K ـ منتظم: گرافی را که درجهٔ تمام رئوس آن با هم مساوی و برابر با عدد k باشند ، گراف k - منتظم می نامیم.
رأس تنها: به رأسی که درجهٔ آن صفر باشد؛ یعنی هیچ یالی به آن متصل نباشد، رأس تنها ( یا ایزوله ) می گوییم. [۴]
گراف تهی: گرافی را که تمام رئوس آن رأس تنها باشند، یعنی هیچ یالی نداشته باشد ، گراف تهی می نامیم. بنابراین منظور از گراف تهیِ n رأسی، گرافی شامل n رأسِ تنها و بدون یال است.
دو رأس مجاور ( همسایه ) : دو رأس u و v را دو رأسِ همسایه یا مجاور گوییم هرگاه توسط یالی به هم وصل شده باشند، یعنیuv ∈ E ( G ) .
مجموعهٔ همسایه های یک رأس: فرض کنیم v ∈ V ( G ) ، به مجموعهٔ رأس هایی از گراف G که به رأس v متصل هستند، "همسایگی باز رأسv " می گوییم و با NG ( v ) نمایش می دهیم. اضافه کردنِ خودِ رأسِ v به NG ( v ) "همسایگی بستهٔ رأسv " را به دست می دهد که آن را با NG[v] نمایش می دهیم. می توان این دو مجموعه را به صورت زیر نمایش داد: NG ( v ) = {u ∈ V ( G ) ∶ uv ∈ E ( G ) } NG[v] =NG ( v ) ∪{v}
دو یال مجاور: دو یال را مجاور گوییم هرگاه رأسی وجود داشته باشد که هر دوی آنها به آن متصل باشند.
بزرگ ترین و کوچک ترین درجۀ یک گراف: بزرگ ترین عدد در بین درجات رئوس گراف G را با∆ ( G ) و کوچک ترینِ آنها را با δ ( G ) نمایش می دهیم و به ترتیب آنها را ماکزیمم و مینیمم درجهٔ گراف می نامیم.
زیرگراف: یک زیرگراف از گراف G گرافی است که مجموعهٔ رئوس آن زیرمجموعه ای از مجموعهٔ رئوس گراف G، و مجموعهٔ یال های آن زیرمجموعه ای از مجموعهٔ یال های G باشد.
مکمل یک گراف: مکمل گرافی مانند G که آن را با G^c یا G ̅ نمایش می دهیم گرافی است که مجموعهٔ رئوس آن همان مجموعهٔ رئوس گراف G است و بین دو رأس از G^cیک یال است اگر و تنها اگر بین همان دو رأس درG یالی وجود نداشته باشد.
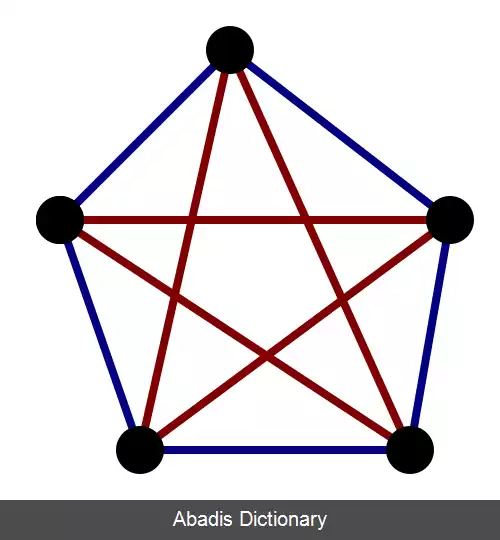
گراف کامل: گرافی را که هر رأس آن با تمام رئوسِ دیگرِ، مجاور باشد گراف کامل می نامیم. گراف کاملِ n رأسی را با Kn نمایش می دهیم. می توان گفت Kn یک گراف n رأسی وn - 1 ــ منتظم است.
مسیر: اگر u و v دو رأس از گراف G باشند، یک مسیر از u به v ( یک v ــ u مسیر ) در G دنباله ای از رئوس دوبه دو متمایز در G است که از u شروع و به v ختم می شود به طوری که هر دو رأس متوالی این دنباله در G مجاور هم باشند. طول یک مسیر برابر است با تعداد یال های موجود در آن مسیر ( یکی کمتر از تعداد رئوس موجود در آن مسیر ) . قرارداد می کنیم که دنبالهٔ متشکل از تنها یک رأسِv، یک مسیر است با طول صفر از رأس v به خودش. ( گرافی را که تنها از یک مسیرِ n رأسی تشکیل شده باشد با Pn نمایش می دهیم ) .
دور: دنبالهٔ ( n ≥ 3 ) v1 v2 v3 . . . vn v1 از رئوس دو به دو متمایز که در آن هر رأس با رأس بعدی مجاور است را یک دور به طول n می نامیم. ( گرافی را که تنها از یک دورِ n رأسی تشکیل شده باشد را با Cn نمایش می دهیم )
همبندی و ناهمبندی یک گراف: گراف G را همبند می نامیم هرگاه بین هر دو رأسِ آن حداقل یک مسیر وجود داشته باشد، در غیر این صورت آن را ناهمبند می نامیم. [۵]
... [مشاهده متن کامل]
گراف جهت دار: منظور از گراف جهت دار گرافی است که یال ها در آن دارای جهت هستند. گراف جهت دار G زوج مرتب ( V, E ) است که V مجموعه ای ناتهی و اعضای E زوجهای مرتب از اعضای V هستند. همانند گرافهای ساده، به اعضایV، راسهای G و به اعضای E، یال های G می گوییم. همچنین به هر گراف جهت دار نموداری در صفحه نسبت می دهیم. به این صورت که به ازای هر راس G نقطه ای در صفحه در نظر می گیریم و به ازای هر یال مانند ( u, v ) کمانی بین u و v رسم می کنیم و روی این کمان فلشی از u به v می گذاریم.
گراف مخلوط: گرافی است که در آن ممکن است برخی یال ها جهت داشته باشند و برخی بدون جهت باشند. گراف مخلوط G، سه تایی مرتب G = ( V, E, A ) است که در آن V مجموعه ی رئوس، E یال های بدون جهت و A یال های جهت دارمی باشند. گراف ساده و گراف جهت دار حالت خاصی از گراف جهت دار می باشند.
گراف وزن دار: گراف وزن دار، گرافی است که به هر یک از یال ها یا به هریک از راس های آن عددی نسبت داده شده است که وزن آن یال یا راس می باشد. وزن یال می تواند نشان دهنده هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد. بعضی از نویسنده ها به گراف وزن دار گراف شبکه ای می گویند.
قرارداد ها:
مرتبه و اندازۀ یک گراف: تعداد رأس های گراف G یعنی |V ( G ) | را مرتبهٔ آن گراف می گوییم و باp ( G ) نمایش می دهیم و تعداد یال های گراف یعنی |E ( G ) | را اندازهٔ گراف G می گوییم و با q ( G ) نمایش می دهیم. معمولاً برای راحتی کار به جای p ( G ) از p و به جای q ( G ) از q استفاده می کنیم.
درجۀ یک رأس: درجهٔ رأس v در گراف G برابر است با تعداد یال هایی از گراف G که به رأس v متصل اند و آن را با degG ( v ) یا به طور ساده تر با deg ( v ) یا d ( v ) نمایش می دهیم. اگر درجهٔ یک رأس فرد باشد آن را رأس فرد و اگر زوج باشد آن را رأس زوج می نامیم.
گراف K ـ منتظم: گرافی را که درجهٔ تمام رئوس آن با هم مساوی و برابر با عدد k باشند ، گراف k - منتظم می نامیم.
رأس تنها: به رأسی که درجهٔ آن صفر باشد؛ یعنی هیچ یالی به آن متصل نباشد، رأس تنها ( یا ایزوله ) می گوییم. [۴]
گراف تهی: گرافی را که تمام رئوس آن رأس تنها باشند، یعنی هیچ یالی نداشته باشد ، گراف تهی می نامیم. بنابراین منظور از گراف تهیِ n رأسی، گرافی شامل n رأسِ تنها و بدون یال است.
دو رأس مجاور ( همسایه ) : دو رأس u و v را دو رأسِ همسایه یا مجاور گوییم هرگاه توسط یالی به هم وصل شده باشند، یعنیuv ∈ E ( G ) .
مجموعهٔ همسایه های یک رأس: فرض کنیم v ∈ V ( G ) ، به مجموعهٔ رأس هایی از گراف G که به رأس v متصل هستند، "همسایگی باز رأسv " می گوییم و با NG ( v ) نمایش می دهیم. اضافه کردنِ خودِ رأسِ v به NG ( v ) "همسایگی بستهٔ رأسv " را به دست می دهد که آن را با NG[v] نمایش می دهیم. می توان این دو مجموعه را به صورت زیر نمایش داد: NG ( v ) = {u ∈ V ( G ) ∶ uv ∈ E ( G ) } NG[v] =NG ( v ) ∪{v}
دو یال مجاور: دو یال را مجاور گوییم هرگاه رأسی وجود داشته باشد که هر دوی آنها به آن متصل باشند.
بزرگ ترین و کوچک ترین درجۀ یک گراف: بزرگ ترین عدد در بین درجات رئوس گراف G را با∆ ( G ) و کوچک ترینِ آنها را با δ ( G ) نمایش می دهیم و به ترتیب آنها را ماکزیمم و مینیمم درجهٔ گراف می نامیم.
زیرگراف: یک زیرگراف از گراف G گرافی است که مجموعهٔ رئوس آن زیرمجموعه ای از مجموعهٔ رئوس گراف G، و مجموعهٔ یال های آن زیرمجموعه ای از مجموعهٔ یال های G باشد.
مکمل یک گراف: مکمل گرافی مانند G که آن را با G^c یا G ̅ نمایش می دهیم گرافی است که مجموعهٔ رئوس آن همان مجموعهٔ رئوس گراف G است و بین دو رأس از G^cیک یال است اگر و تنها اگر بین همان دو رأس درG یالی وجود نداشته باشد.
گراف کامل: گرافی را که هر رأس آن با تمام رئوسِ دیگرِ، مجاور باشد گراف کامل می نامیم. گراف کاملِ n رأسی را با Kn نمایش می دهیم. می توان گفت Kn یک گراف n رأسی وn - 1 ــ منتظم است.
مسیر: اگر u و v دو رأس از گراف G باشند، یک مسیر از u به v ( یک v ــ u مسیر ) در G دنباله ای از رئوس دوبه دو متمایز در G است که از u شروع و به v ختم می شود به طوری که هر دو رأس متوالی این دنباله در G مجاور هم باشند. طول یک مسیر برابر است با تعداد یال های موجود در آن مسیر ( یکی کمتر از تعداد رئوس موجود در آن مسیر ) . قرارداد می کنیم که دنبالهٔ متشکل از تنها یک رأسِv، یک مسیر است با طول صفر از رأس v به خودش. ( گرافی را که تنها از یک مسیرِ n رأسی تشکیل شده باشد با Pn نمایش می دهیم ) .
دور: دنبالهٔ ( n ≥ 3 ) v1 v2 v3 . . . vn v1 از رئوس دو به دو متمایز که در آن هر رأس با رأس بعدی مجاور است را یک دور به طول n می نامیم. ( گرافی را که تنها از یک دورِ n رأسی تشکیل شده باشد را با Cn نمایش می دهیم )
همبندی و ناهمبندی یک گراف: گراف G را همبند می نامیم هرگاه بین هر دو رأسِ آن حداقل یک مسیر وجود داشته باشد، در غیر این صورت آن را ناهمبند می نامیم. [۵]
گراف: [اصطلاح شبکه ریلی] نمودار حرکت مکانی قطار وسایر ( وسائط نقلیه ریلی ) در بعد زمان را گراف می گویند که در آن زمان و مکان حرکت ، توقف ، تلاقی ، سبقت ، مشخصات وسایط نقلیه ریلی و تمام عملیات سیر و حرکتی محور حرکت با درج کد مربوطه ثبت و ترسیم می گردد.
نمودار
