کمان

/kamAn/

مترادف کمان: شیز، قوس، کمانه، گوژ، وتر

معنی انگلیسی:

unstrung, arc, arch, bow, crescent, longbow, old name of

لغت نامه دهخدا

کمان. [ ک َ ] ( اِ ) معروف است و به عربی قوس خوانند. ( برهان ). ترجمه قوس و مبدل خمان مرکب از «خم » و «ان » که کلمه نسبت است و کشیده و خمیده و سخت و نرم و گسسته پی و کژابرو و بازوشکن از صفات و ابرو از تشبیهات اوست و به دمشق و چاچ و افراسیاب و رستم و کیان مخصوص. ( از آنندراج ). و در اصل خمان بوده به جهت خمیدگی خمان خواندند. ( انجمن آرا ). هر چوب خمیده ای که از یک سر آن تا به سر دیگرش زهی سخت محکم بسته باشند و به تازی قوس گویند. ( ناظم الاطباء ). شیز. ( صحاح الفرس ، یادداشت به خط مرحوم دهخدا ). پهلوی ، کمان و کمان وریه ( کمانداری ). کردی ، کوان . سلاحی که در قدیم ( و هنوز در بعضی قبایل ) برای تیر انداختن بکار می رفت و آن مرکب بود از چوبی خمیده که دو سر آن را به وسیله زهی سخت محکم می بستند و آن سلاحی بود در قدیم که برای پرتاب کردن تیر بکار می رفت و آن را از چوب ( یا چیزی نظیر آن ) می ساختند بدین طریق که به دو طرف آن زهی می بستند تا به شکل قریب به نیم دایره در آید. ( حاشیه برهان چ معین ). قوس. سلاحی که در قدیم برای تیر انداختن بکار می رفت و آن مرکب بود از چوبی نرم و خمیده به شکل ابروان که به وسیله زهی سخت دو انتهای آن را به یکدیگر محکم می بستند و بدان در قدیم تیراندازی می کردند ( هنوز نیز در میان بعضی قبایل بدوی متداول است ). امروزه هم تیراندازی با کمان جزو ورزشهای متداول بشمار می رود. کمانهای جنگی قدیم را از قطعات استخوان می ساخته اند و روی آن را پی پیچ می کرده اند و برای آنکه حالت فنری پیدا کند روغن مخصوصی به خورد آن می داده اند و هنوز هم روغنی به نام «روغن کمان »هست که بمصرف می رسد. کمانهای سابق به دو شکل ساخته می شده : یک نوع مقوس و یک نوع مستقیم که در طرفین مقبض آن برآمدگی داشت. کمانهای مستقیم را «کمان چهارخم »می گفته اند، زیرا از یک طرف دو خمیدگی برجسته و از طرف دیگر دو خمیدگی گود داشته. ( فرهنگ فارسی معین ). اسباب جنگ و شکار ایام قدیم است که از چوب یا شاخ یا فولاد ساخته می شد. ( از قاموس کتاب مقدس ) :
میغ چون ترکی آشفته که تیر اندازد
برق تیر است مر او رامگر و رخش کمان.

فرالاوی ( یادداشت به خط مرحوم دهخدا ).

دوان شد به میدان شاه اردشیر
کمانی به یک دست و دیگر دو تیر.

فردوسی.

کمانی به بازو درافکند سخت
یکی تیر بر سان شاخ درخت.بیشتر بخوانید ...

فرهنگ فارسی

چوبی خمیده که دوسر آن رابازه محکم بسته وبکشند، آلتی که برای تیراندازی بکارمیرفته، هرچیزخمیده راگویند، خمان هم گویند
( اسم ) ۱ - سلاحی که در قدیم برای تیر انداختن بکار میرفت و آن مرکب بود از چوبی نرم و خمیده بشکل ابروان که بوسیل. زهی سخت دو انتهای آنرا بیکدیگر محکم می بستند و بدان در قدیم تیر اندازی میکردند ( هنوز نیز در میان بعضی قبایل بدوی متداول است ) . امروزه هم تیر اندازی با کمان جزو ورزشها ی متداول بشمار میرود قوس . توضیح کمانهای جنگی قدیم را از قطعات استخوان میساخته اند و روی آنرا پی پیچ میکرده اند و برای آنکه حالت فنری پیدا کند روغن مخصوصی بخورد آن میداده اند و هنوز هم روغنی بنام روغن کمان هست که بمصرف میرسد . کمانها ی سابق بدو شکل ساخته میشده : یک نوع مقوس و یک نوع مستقیم که در طرفین مقبض آن بر آمدگی داشت . کمانهای مستقیم را کمان چهار خم میگفته اند زیرا از یک طرف دو خمیدگی بر جسته و از طرف دیگر دو خمیدگی گود داشته . یا ترکیبات اسمی : چرخ کمان . چرخی بود که بوسیل. آن تمرین کنند. تیر اندازی پی در پی تیر می انداخت . یا کمان آسمان . آسمان ( سپهر ) که بشکل کمان است . یا کمان بهمن قوس قزح . یا کمان چرخ . ۱ - یکی از آلات قلعه گیری . ۲ - قوس قزح . یا کمان حکمت . نوعی منجنیق که بدان تیر می انداختند . یا کمان حلقه . کمانی که هنوز آنرا زه نکرده باشند : ( بکیش هوشمند تان خود نمایی نیست دستورم کسی آگه نباشد چون کمان حلقه از زورم ) ( شفیع اثر ) یا کمان راه آهن . راه خمدارو پیچا پیچ یا کمان رستم . قوس قزح : ( از باد و باران و تذرگ و تند و هده و درخش و صاعقه و کمان رستم ... ) . ( بجز او که زیر آرد ز فلک کمان رستم در چاره را گرفته بمصاف هفتخوانی ? ) ( نظیری نیشابوری ) یا کمان زنبوری . تفنگ بندق : ( گرفتند گردان ایران زمین کمانهای زنبوری چرخ کین ) . ( منسوب به فردوسی ) توضیح در فهرست ولف نیامده . یا کمان سام . قوس قزح . یا کمان شیطان . ۱ - قوس متعلق به ابلیس : ( خدنگ غمزه بجز قصد اهل دین نکند حذر که ابروی خوبان کمان شیطانست ) . ( محمد سلیم ) ۲ - آسمان سپهر : ( خطر ز حادثه پیش است گوشه گیران را که این سپهر مقرنس کمان شیطانست ) . ( عبد الغنی قبول ) ۳ - قوس قزح : ( رنگین تو کنی کمان شیطان چون طاس مقرنس سلیمان ) . ( تحفه العراقین ) یا کمان صدمن ( صدمنی ) . کمان بسیار قوی و سخت که بازور بسیار آنرا توان کشید : ( چون کمان صدمنی در دست تو گردد بلند چون خدنگ دیده دوز از شست تو گرد دروان ... ) . ( معزی ) یا کمان فولاد . کمانی که پهلوانان کشند و چل. آن از زنجیر باشد . یا کمان مهره . کمان مهره اندازی کمان گلوله کمان گروهه یا کمان از طاق بلند آویختن . دعوی کمال کردن : ( ز زور طبع معنی آفرین صائب . طمع دارم که از طاق بلند عرش آویزد کمان من ) . ( صائب ) یا کمان بخم آوردن . کمان افراشتن : ( ژاله سپر برف ببرد از کتف کوه چون رستم نیسان بخم آورد کمان را ) . ( انوری ) یا کمان بر سر کسی زدن . تیر بسوی او پرتاب کردن : ( مژگان تو خنجر برخ ماه کشیده ابروت زده برسر خورشید کمان را ) . ( کلیم ) یا کمان بطاق بلند آویختن ( گذاشتن ) . دعوی کمال کردن : ( بر چرخ این هلال نباشد که دست تو آویخته بطاق بلندی کمان تو ) . ( کلیم ) یا کمان بلند ساختن ( کردن ) . برداشتن کمان بقصد تیر اندازی : ( کمان ز نیر اعظم چگونه خواهم من که ذره ای نتوانم بلند کرد از جاش ) . ( ملک مشرقی ) یا کمان پرکش کردن . کشیدن کمان تا بحدی که معهود استادان این فن است و ما فوق آن متصور نباشد تیر پرکش زدن : ( چون کمانی را که پرکش کرده باشی سر دهی نیستی میاید ار دنبال هستی میرود ) . ( باقر کاشی ) یا کمان پیش کردن . مجهز شدن بکمان برای تیر اندازی : ( بصید افکنی چون کمان کرد پیش فرو ریخت صد تیر بر صید خویش ) . ( طغرا ) یا کمان را بزه کردن . زه کمان را بجای خود بستن مقابل از کمان گشودن . توضیح سابقا معمول بوده که پس از تیر اندازی زه را می گشودند تا کمان قابلیت ارتجاع خود را از دست ندهد و چون احتیاج بتیراندازی داشتند زه را در کمان میکردند: ( کمان را بزه کرد و اندر کشید ) . یا کمان چیزی را بزه کردن آن چیز را سخت بکار بردن : ( بوسهل زوزنی کمان قصد و عصبیت بزه کرد و هیچ بد گفتن بجایگاه نیفتد ) . یا کمان را چاشنی کردن . معلوم کردن زور کمان و آن چنان باشد که اندک بکشند و باز رها کنند یا کمان را چله کردن . آماده کردن کمان برای تیر اندازی : ( این کمان را از زبردستان که خواهد چله کرد باد. پر زور چون نگشود ز ابر و چین ترا ) . ( صائب ) یا کمان کسی را کشیدن . هماورد او شدن از عهد. او بر آمدن : ( نقاش بیحد است ولی کو مصوری تا یک ادای ابروی او را کشد کمان ? ) ( مفید بلخی ) یا کمان کسی را نتوانستن کشیدن . ۱ - از عهد. او بر آمدن نتوانستن : ( بازوی بخت من آن طور قوی ساخته اند که کمانم نکشد رستم فولاد کمان ) . ( شانی تکلو ) ۲ - برج نهم . ۳ - قسمی ساز از جنس رباب که بشکل کمان است کمانه . ۴ - کمان کوچک که مضراب ساز است کمانه آرشه . ۵ - شکل کمان که از خط طغرا بالا ی فرمانها ی شاهی پیدا میشد کمانچ. طغرا .
از دیه های کوزدر

فرهنگ معین

(کَ ) [ په . ] (اِ. ) وسیله ای برای تیراندازی در قدیم . ، ~به زه بودن کنایه از: آمادة نبرد بودن .

فرهنگ عمید

۱. نوعی سلاح جنگی چوبی و خمیده که برای پرتاب کردن تیر به کار می رفت.
۲. چوبی بلند و سرکج برای جدا کردن الیاف پنبه یا پشم از یکدیگر.
۳. (نجوم ) = قوس
۴. (موسیقی ) [قدیمی] آرشه.
۵. (موسیقی ) [قدیمی] سازی زهی شبیه رباب و به شکل کمان.
* کمان چاچی: [قدیمی] نوعی کمان مرغوب که در چاچ (نام قدیم تاشکند ) ساخته می شد: پیاده ز بهرام بگریختند / کمان های چاچی فرو ریختند (فردوسی: ۸/۱۳۶ )، کمان های چاچی و تیر خدنگ / سپرهای چینی و ژوبین جنگ (فردوسی: ۱/۱۲۷ ).
* کمان رستم: [قدیمی، مجاز] = رنگین کمان
* کمان گشادن: (مصدر متعدی ) به دست گرفتن کمان و کشیدن زه آن و تیر انداختن.

فرهنگستان زبان و ادب

{arc , arch} [معماری و شهرسازی] خط منحنی بسیط یا پاره ای از دایره یا دیگر مقاطع مخروطی
{bow} [ورزش] قطعۀ منحنی شکلی از پلاستیک یا هر مادۀ کشسان دیگر که دو سر آن به وسیلۀ زه به هم متصل شده است
{catenary} [حمل ونقل دریایی] انحنای زنجیر معلق بین دو تکیه گاه یا میان دو شناور درحالت یدک کشی یا بین کشتی و بستر دریا
[ریاضی] ← پرانتز

گویش مازنی

/kemaan/ وسیله ای برای باز کردن چشم

واژه نامه بختیاریکا

کیوار؛ کِیُو

دانشنامه عمومی

کمان (جنگ افزار). کَمان گونه ای جنگ افزار باستانی است که با نیروی ذخیره شده در زه خود پیکان را به جلو پرتاب می کند. کمان از گذشته تاکنون در زمینهٔ شکار، ورزش و جنگ کارایی داشته است، اگرچه با ساخت و توسعه تفنگ از اهمیتش بسیار کاسته شده است.
کهنترین قطعات مربوط به یک کمان در شمال آلمان یافت شد و دیرینگی اش را مربوط به ۸ هزار سال پیش از میلاد مسیح دانسته اند. این آثار در خلال جنگ جهانی دوم نابود شد و چون تا آن زمان آزمایش کربن ۱۴ هنوز اختراع نشده بود پس نمی توان به تاریخ یادشده اطمینان داشت. پس از آن کهنترین ترین کمان ها در شمال دانمارک کشف شده و تاریخش به ۶هزار سال پیش از میلاد بازمی گردد. اوتسی مرد یخی - که پیکرش در مرز میان اتریش و ایتالیا پیداشد - بر اثر فرورفتن یک پیکان در شش اش کشته شده بود و زمان مرگش هم به ۳۳۰۰ سال پیش از میلاد بازمی گردد. به نوک تیر پیکان می گفتند و به ته تیر پر عقاب می بستند.

wiki: کمان (جنگ افزار)

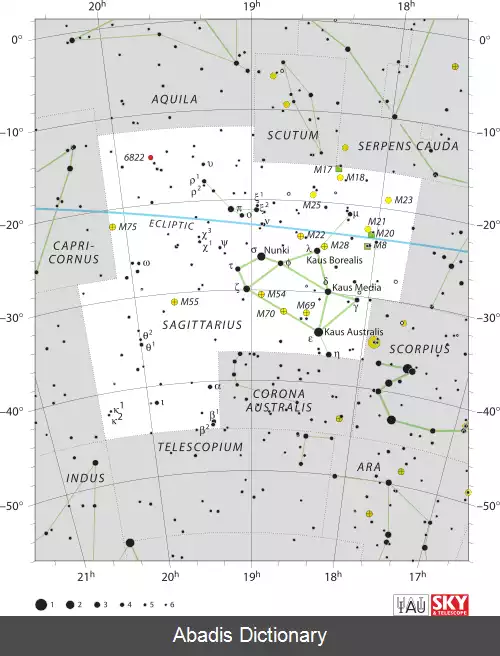
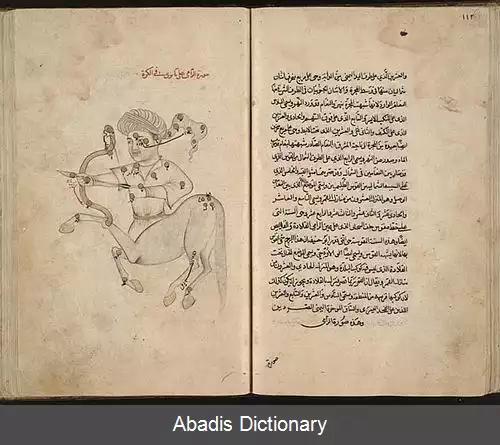
کمان (صورت فلکی). صورت فلکی کمان یا قوس ( معادل لاتین:Sagittarius ) ( کمانگیر ) با مساحت: ۸۶۷ درجه مربع ( پانزدهمین ) در صورت های فلکی منطقةالبروج ( زودیاک ) قرار دارد. این صورت فلکی به شکل پیکان، یکی از ۴۸ صورت فلکی ذکر شده توسط اخترشناس سدهٔ دوم بطلمیوس نیز هست و امروز یکی از ۸۸ صورت فلکی در اخترشناسی مدرن ثبت است. در منابع یونانی و لاتین صورت فلکی کمان بیشتر به صورت یک سانتور که کمان را به عقب می کشد، نشان داده می شود.
کمان یا درست تر کمان دار موجودی نیمی انسان ٬نیمی بز یا حیوانی با بالاتنه انسان و پایین تنه اسب معرفی شده است. مردان اسب پیکر sagittarius همگی موجوداتی ظالم و خوشگذران بودند ولی شیرون یک استثنا بود. او فنون جنگی از قبیل تیراندازی را به جوانانی که بعدها قهرمان می شدند می آموخت. روزی هرکول او را ناخواسته با تیری زهرآلود زد. او از موهبت فناناپذیری چشم پوشید و پس از مدتی زئوس به او اجازهٔ مرگ داد و او را به صورت یک صورت فلکی در آسمان قرار داد. [ ۱]
اپسیلون قوس به نام کمان جنوبی دارای طیف B9 IV و در فاصله ۸۵ سال نوری از ماست. این ستاره با قدر۱٫۹٬درخشانترین ستاره صورت فلکی قوس محسوب می گردد. نزدیکترین ستاره صورت فلکی قوس به ما:رز ۱۵۴ ( ۹٫۶۸ سال نوری )
این صورت فلکی دارای ۱۵ جرم مسیه می باشد دلیلش هم این است که در راستای کهکشان راه شیری قرار دارد.
• مسیه ۸
• مسیه ۱۷
• مسیه ۱۸
• مسیه ۲۰
• مسیه ۲۱
• مسیه ۲۲
• مسیه ۲۳
• مسیه ۲۴
• مسیه ۲۵
• مسیه ۲۸
• مسیه ۵۴
• مسیه ۵۵
• مسیه ۶۹
• مسیه ۷۰
• مسیه ۷۵
• دلو
• سپر
• کژدم
• تاج جنوبی
• بزغاله

wiki: کمان (صورت فلکی)

کمان (فیلم ۲۰۰۵). کمان ( کره ای: 활 ) فیلمی به نویسندگی و کارگردانی کیم کی دوک محصول سال ۲۰۰۵ است. این فیلم مانند دیگر فیلم های کیم کی دوک، دیالوگ های بسیار کمی دارد و مملو از نمادها است. [ ۱]
برای حدود ۱۰ سال، یک دختر ۱۶ ساله و یک پیرمرد در یک کشتی کوچک لنگرانداخته در دریای آزاد که مکانی شناخته شده برای ماهی گیران مبتدی است زندگی می کنند. آن ها قصد دارند در سالگرد ۱۷ سالگی دختر با یکدیگر ازدواج کنند اما وقتی تیمی از ماهی گیران از جمله یک دانشجوی جوان از کشتی بازدید می کنند این برنامه دچار مشکل می شود. [ ۲]
کمان در سال ۲۰۰۵ در جشنواره فیلم کن حضور داشت و در بخش نوعی نگاه نامزد بهترین فیلم شد.
• کمان در بانک اطلاعات اینترنتی فیلم ها ( IMDb )

wiki: کمان (فیلم ۲۰۰۵)

کمان (هندسه). در هندسه، یک کمان بخشی از یک خم مشتق پذیر در صفحهٔ دو بعدی است. برای نمونه یک کمان دایره ای ( کمان مستدیر ) ، بخشی از پیرامون یک دایره است. اگر کمان بخشی از یک دایرهٔ بزرگ ( دایره عظیمه ) یا بیضی بزرگ ( بیضی عظیمه ) باشد آن را کمان بزرگ ( کمان عظیمه ) می نامیم.
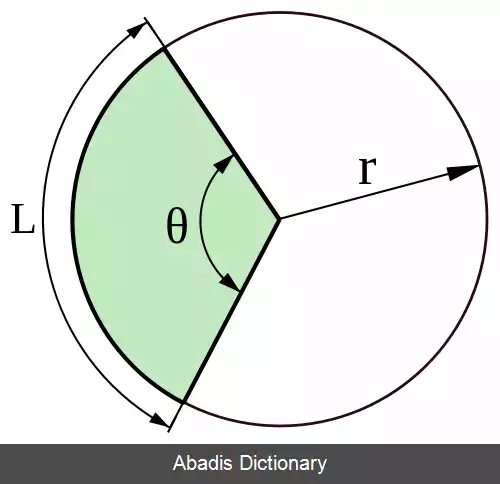
کمانی از دایره به شعاع r که زاویه ای مرکزی به نام θ را دربر می گیرد ( به رادیان ) به این معنی که اضلاع زاویه شعاع هایی از دایره اند، در این صورت طول آن کمان برابر با θ r خواهد بود. دلیل این مطلب عبارت است از:
پس از جایگذاری مقدار محیط دایره خواهیم داشت:
مقدار L نسبت به θ این گونه به دست می آید:
اگر زاویه ای α درجه باشد مقدار آن به رادیان خواهد بود:
پس طول کمان می شود:
راه دیگر بدست آوردن طول یک کمان دایره ای این است که دو سر آن کمان را به مرکز دایره وصل کنیم و زاویهٔ تولید شده در مرکز دایره را اندازه بگیریم، نسبت زاویهٔ تولید شده به °۳۶۰ برابر است با نسبت طول کمان به پیرامون دایره. برای نمونه اگر زاویهٔ تولید شده ۶۰ درجه باشد و محیط دایره ۲۴ سانتی متر، طول کمان خواهد شد:
سطح میان یک کمان و مرکز دایره عبارت است از:
نسبت سطح: A به سطح کل دایره برابر است با نسبت زاویهٔ θ به زاویهٔ کل دایره:
π از دو طرف تساوی ساده می شود آنگاه:
دو طرف تساوی را در r 2 ضرب می کنیم:
اگر زاویه بجای رادیان به درجه داده شده بود، سطح کمان آن می شد:
سطح میان کمان دایره و پاره خط رسانندهٔ دو سر کمان به یکدیگر عبارت است از:
برای بدست آوردن سطح قطاع دایره باید مساحت مثلث تولید شده در مرکز دایره ( با ضلع های شعاع دایره ) را از مساحت کمان که در بالا توضیح داده شد کم کنیم.
با استفاده از نظریهٔ سکانت - تانژانت یا توان یک نقطه می توان شعاع r یک دایره را با استفاده از درازای H و پهنای W یکی از کمان های آن به صورت زیر بدست آورد:

wiki: کمان (هندسه)

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف

دانشنامه آزاد فارسی

کَمان (arc)
در هندسه، بخشی از دایره یا منحنی. هر قطر دایره آن را به دو کمان تقسیم می کند که نیم دایره نامیده می شوند و هر یک دقیقاً نیمی از دایره اند. هر وترِ دایره دو کمان پدید می آورد که یکی کوچک تر از نیم دایره، موسوم به کمان اقصر یا کوچک تر، و دیگری بزرگ تر از نیم دایره، موسوم به کمان اطول یا بزرگ تر، است. کمان های دایره را برحسب درجه یا رادیان اندازه گیری می کنند. اندازۀ هر کمان برابر با اندازۀ زاویۀ مرکزی مقابل آن است که از وصل کردن مرکز دایره به دو انتهای کمان ایجاد می شود. بنابراین، نیم دایره ْ۱۸۰ یا π رادیان، کمانِ کوچک تر همواره کمتر از ْ۱۸۰ و کمان بزرگ تر همواره بیشتر از ْ۱۸۰ و کمتر از ْ۳۶۰ است.

wikijoo: کمان

کمان (زمین شناسی). رجوع شود به:قوس (زمین شناسی)

wikijoo: کمان_(زمین_شناسی)

جدول کلمات

قوس

مترادف ها

bow (اسم)

سجود، قوس، کمان، تعظیم

arc (اسم)

قوس، کمان، هلال، جرقه، خم، خرپشته

arch (اسم)

قوس، کمان، طاق

fiddlestick (اسم)

کمان، ارشه ویولون، ارشه، چیز بی معنی یا پوچ

فارسی به عربی

قوس

پیشنهاد کاربران

برما بسی کمان ملامت کشیده اند.

کمان؛
در لرستان می گویند" برایم در کمان نگذار. "
حافظ در شیراز می فرماید؛
برما بسی کمان ملامت کشیده آن.
شاید در شیراز می گفته اند ؛" برایم کمان نکش".

واژه کمان
معادل ابجد 111
تعداد حروف 4
تلفظ [kamān]
نقش دستوری اسم
ترکیب ( اسم ) [پهلوی: Kamān] ‹خمان›
مختصات ( کَ ) [ په . ] ( اِ. )
آواشناسی kamAn
الگوی تکیه WS
شمارگان هجا 2
... [مشاهده متن کامل]

منبع لغت نامه دهخدا
فرهنگ فارسی عمید
فرهنگ فارسی معین
فرهنگ واژه های سره
فرهنگ فارسی هوشیار

وسیله ی تیر اندازی

کمان در ترکی اوک یا اوخ و قاش هست

به جای کروشه کمان

کمان از ریشه "خمان" است به معنی "خم شده" و واژه ای پارسی می باشد.

بگسست. پاره شدن

شیز، قوس، کمانه، گوژ، وتر

کمان : تحریف خمان است ، خم به معنای دولا شدن و ( ان ) آخر پسوند خصلت می باشد.

کمان لاری. نوعی کمان که تا پیش از صفویه از اقلام صادراتی لارستان به هندوستان و شیلاو. ( کره ) و افریقا بود که خوشدست تر و دقیقتر از کمان ترکی. شهرت جهانی داشت و در سفرنامه سیلویا فیگوئرا و پیترو دلاواله به ان اشاره شده

مشاهده ادامه پیشنهادها (١٠ از ١١)

+ عکس و لینک

بپرس

سوالت رو اینجا بپرس همه سوال ها