کلاس هم ارزی

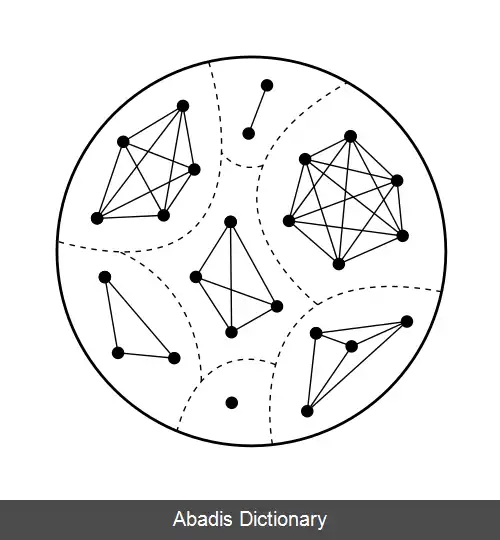
در ریاضیات، اگر عناصر یک مجموعه S دارای یک مفهوم هم ارزی باشند ( که این موضوع توسط یک رابطه هم ارزی صوری سازی می شود ) ، آنوقت می توان مجموعه S را به کلاس های هم ارزی تجزیه کرد. این کلاس های هم ارزی به این شیوه ساخته می شوند که عناصر a و b به یک کلاس هم ارزی تعلق دارند، اگر و تنها اگر، با هم هم ارز باشند.
به صورت صوری، اگر یک مجموعه S و یک رابطه هم ارزی ∼ روی S تعریف شده باشد، کلاس هم ارزی یک عنصر a در S که توسط [ ۱] نشان داده می شود، برابر مجموعه زیر است:[ ۲] { x ∈ S : x ∼ a } برای عناصری که با a هم ارز هستند. این موضوع از ویژگی های تعریف کننده روابط هم ارزی قابل اثبات است، که در آن کلاس های هم ارزی یک افراز از S می سازد. این افراز ( یعنی مجموعه کلاس های هم ارزی ) را گاهی مجموعه خارج قسمتی، یا فضای خارج قسمتی برای S توسط ∼ هم می نامند و توسط S / ∼ نشان داده می شود. وقتیکه مجموعه S یک ساختار دارد ( مثل یک عمل گروهی یا یک توپولوژی ) و نیز رابطه هم ارزی ∼ با این ساختار سازگار است، آنوقت مجموعه خارج قسمتی معمولاً ساختار مشابهی از مجموعه والد خود به ارث می برد. مثال های آن شامل فضاهای خارج قسمتی در جبر خطی، فضاهای خارج قسمتی در توپولوژی، گروه های خارج قسمتی، فضاهای همگن، حلقه های خارج قسمتی، مونویدهای خارج قسمتی، و رده های خارج قسمتی است.
• اگر X {\displaystyle X} برابر مجموعه همه خودروها باشد، و ∼ {\displaystyle \, \sim \, } برابر رابطه هم ارزی «دارای رنگ مشابه اند» باشد، آنوقت یک کلاس هم ارزی خاص شامل خودروهای سبز است و X / ∼ {\displaystyle X/\sim } همان مجموعه همه رنگ های خودروها است.
• فرض کنید که X {\displaystyle X} مجموعه همه مستطیل ها در یک صفحه باشد، و ∼ {\displaystyle \, \sim \, } برابر رابطه هم ارزی «دارای مساحت مشابه اند» باشد، آنوقت برای هر عدد حقیقی مثبت A {\displaystyle A} ، یک کلاس هم ارزی برای همه مستطیل هایی که مساحتی برابر A {\displaystyle A} دارند، موجود است. [ ۳]
• رابطه هم ارزی پیمانه ۲ را روی مجموعه اعداد صحیح Z {\displaystyle \mathbb {Z} } به این صورت که x ∼ y {\displaystyle x\sim y} اگر و فقط اگر تفاضل آن ها یعنی x − y {\displaystyle x - y} یک عدد زوج باشد. این رابطه به دقیقاً کلاس هم ارزی منجر می شود: یک کلاس شامل همه اعداد زوج، و دیگری شامل همه اعداد فرد است. به کمک قلاب مربعی دور یک عضو کلاس برای نشان دادن یک کلاس هم ارزی تحت این رابطه، , , {\displaystyle , , } و {\displaystyle } همه یک عنصر مشابه برای Z / ∼ {\displaystyle \mathbb {Z} /\sim } را نشان می دهند. [ ۴]
• فرض کنید X {\displaystyle X} برابر مجموعه همه زوج مرتب های اعداد صحیح ( a , b ) {\displaystyle ( a, b ) } با b {\displaystyle b} غیرصفر باشد؛ و یک رابطه هم ارزی ∼ {\displaystyle \, \sim \, } روی X {\displaystyle X} تعریف کنیم به این صورت که ( a , b ) ∼ ( c , d ) {\displaystyle ( a, b ) \sim ( c, d ) } اگر و فقط اگر a d = b c , {\displaystyle ad=bc, } باشد، آنوقت کلاس هم ارزی برای زوج ( a , b ) {\displaystyle ( a, b ) } را می توان توسط عدد گویای a / b {\displaystyle a/b} شناساند؛ و از این رابطه هم ارزی و کلاس های هم ارزی آن می توان استفاده کرد تا به یک تعریف صوری از مجموعه اعداد گویا رسید. [ ۵] از همین ساختار را می توان به میدان نسبتی برای هر حوزه صحیح تعمیم داد.
• اگر X {\displaystyle X} شامل همه خطوط، مثلاً در فضای اقلیدسی، باشد، و L ∼ M {\displaystyle L\sim M} به معنی آن باشد که L {\displaystyle L} و M {\displaystyle M} دو خط موازی هستند، آنوقت مجموعه خطوطی که با هم موازی اند یک کلاس هم ارزی می سازد، مادامیکه یک خط با خودش موازی درنظر گرفته می شود. در این حالت، هر کلاس هم ارزی یک نقطه در بینهایت را معین می کند.