کدگذاری[ ۱] گولومب ( به انگلیسی: Golomb coding ) یا رمزگذاری گولومب یک روش فشرده سازی بدون اتلاف اطلاعات است از خانواده ای از رمزهای فشرده سازی داده که توسط سلیمان دبلیو گلومب در دهه 1960 ابداع شده است. حروف الفبایی از یک توزیع هندسی تبعیت می کنند، از رمزنگاری Golomb به عنوان یک رمز پیشوندی مطلوب استفاده می کنند[ ۲] . باعث می شود که رمزگذاری Golomb بسیار مناسب برای موقعیت هایی باشد که در آن احتمال وقوع مقادیر کوچک در جریان ورودی، به طور قابل توجهی نسبت به مقادیر بزرگ بیشتر است.
رمزگذاری Rice ( اختراع شده توسط رابرت اف. رایس ) به استفاده از زیرمجموعه ای از خانواده کدهای Golomb، برای تولید یک رمز پیشوندی ساده تر ( اما نه لزوما بهینه ) اشاره دارد. رایس از این مجموعه رمزها در یک قالب رمز گذاری انطباقی استفاده کرد. منظور از "رمزگذاری رایس" همچنین می تواند آن قالب رمزگذاری انطباقی و یا استفاده از آن زیر مجموعه از کدهای Golomb باشد. در حالی که رمزگذاری Golomb دارای یک پارامتر قابل تنظیم است که می تواند هر عدد صحیح مثبت باشد، کدهای رایس آن هایی هستند که پارامتر قابل تنظیم آن، عددی به صورت 2 n است. از آنجایی که کامپیوتر ها با منطق دودویی کار می کنند، این امر باعث می شود تا رمزگذاری رایس برای استفاده در کامپیوتر بسیار راحت باشد زیرا به راحتی می توان آن را در عدد 2 ضرب و تقسیم کرد.
رایس بسیار علاقه مند بود تا این زیرمجموعه ساده تر را ارائه کند؛ به این دلیل که توزیع های هندسی اغلب با زمان تغییر می کنند، یا که دقیقاً شناخته شده نیستند و یا هر دو. بنابراین انتخاب رمز به ظاهر بهینه ممکن است چندان سودمند نباشد.
رمزگذاری رایس به عنوان مرحله رمزگذاری آنتروپی در تعدادی از روش های فشرده سازی تصویر بدون اتلاف و فشرده سازی داده های صوتی استفاده می شود.
رمزگذاری Golomb از یک پارامتر قابل تنظیم M برای تقسیم مقدار ورودی N به دو بخش استفاده می کند: q ، نتیجه تقسیم توسط M و r ، باقی مانده. خارج قسمت در قالب رمزگذاری یگانی ( unary ) و به دنبال آن مقدار باقی مانده در رمزگذاری دودویی منقطع قرار می گیرد. اگر M = 1 باشد، کدگذاری Golomb معادل کدگذاری یگانی است.
رمزهای Golomb - Rice را می توان به عنوان رمزهایی در نظر گرفت که عددی را مشخص می کند که در موقعیت b i n ( q ) ، و آفست b i n ( q ) قرار دارد. شکل بالا موقعیت q و افست r را برای رمزگذاری عدد صحیح N با استفاده از پارامتر M در روش Golomb - Rice را نشان می دهد.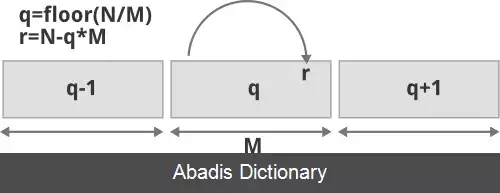
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفرمزگذاری Rice ( اختراع شده توسط رابرت اف. رایس ) به استفاده از زیرمجموعه ای از خانواده کدهای Golomb، برای تولید یک رمز پیشوندی ساده تر ( اما نه لزوما بهینه ) اشاره دارد. رایس از این مجموعه رمزها در یک قالب رمز گذاری انطباقی استفاده کرد. منظور از "رمزگذاری رایس" همچنین می تواند آن قالب رمزگذاری انطباقی و یا استفاده از آن زیر مجموعه از کدهای Golomb باشد. در حالی که رمزگذاری Golomb دارای یک پارامتر قابل تنظیم است که می تواند هر عدد صحیح مثبت باشد، کدهای رایس آن هایی هستند که پارامتر قابل تنظیم آن، عددی به صورت 2 n است. از آنجایی که کامپیوتر ها با منطق دودویی کار می کنند، این امر باعث می شود تا رمزگذاری رایس برای استفاده در کامپیوتر بسیار راحت باشد زیرا به راحتی می توان آن را در عدد 2 ضرب و تقسیم کرد.
رایس بسیار علاقه مند بود تا این زیرمجموعه ساده تر را ارائه کند؛ به این دلیل که توزیع های هندسی اغلب با زمان تغییر می کنند، یا که دقیقاً شناخته شده نیستند و یا هر دو. بنابراین انتخاب رمز به ظاهر بهینه ممکن است چندان سودمند نباشد.
رمزگذاری رایس به عنوان مرحله رمزگذاری آنتروپی در تعدادی از روش های فشرده سازی تصویر بدون اتلاف و فشرده سازی داده های صوتی استفاده می شود.
رمزگذاری Golomb از یک پارامتر قابل تنظیم M برای تقسیم مقدار ورودی N به دو بخش استفاده می کند: q ، نتیجه تقسیم توسط M و r ، باقی مانده. خارج قسمت در قالب رمزگذاری یگانی ( unary ) و به دنبال آن مقدار باقی مانده در رمزگذاری دودویی منقطع قرار می گیرد. اگر M = 1 باشد، کدگذاری Golomb معادل کدگذاری یگانی است.
رمزهای Golomb - Rice را می توان به عنوان رمزهایی در نظر گرفت که عددی را مشخص می کند که در موقعیت b i n ( q ) ، و آفست b i n ( q ) قرار دارد. شکل بالا موقعیت q و افست r را برای رمزگذاری عدد صحیح N با استفاده از پارامتر M در روش Golomb - Rice را نشان می دهد.



wiki: کدگذاری گولومب
