در ریاضیات، به بیان کلی می توان گفت که تابع f پیوسته یکنواخت ( به انگلیسی: Uniformly Continuous ) است اگر بتوان تضمین کرد که با نزدیک کردن x و y به میزان کافی به یکدیگر، f ( x ) و f ( y ) را به میزان دلخواه به همدیگر نزدیک نمود؛ برعکس پیوستگی عادی توابع، که در آن فاصله بیشینه بین f ( x ) و f ( y ) ممکن است به خود x و y وابسته باشد.
اگر توابع پیوسته روی دامنه متناهی بی کران باشند ممکن است به طور یکنواخت پیوسته نباشند همچون f ( x ) = 1 x روی ( 0 , 1 ) ، یا در حالتی که شیب خطوط مماس بر تابع مورد نظر بی کران باشند همچون f ( x ) = x 2 روی خط حقیقی. با این حال، هر نگاشت لیپشیتز بین فضاهای متری به طور یکنواخت پیوسته است، بخصوص هر ایزومتری ( نگاشت حافظ فاصله ) پیوسته یکنواخت است.
گرچه که پیوستگی عادی را می توان برای توابع روی فضای توپولوژی تعریف نمود، ولی تعریف پیوستگی یکنواخت برای چنین توابعی نیازمند ساختارهای بیشتری ست. این مفهم به اندازه همسایگی های نقاط مجزا وابسته بوده، بنابراین نیازمند فضای متری یا در حالت کلی تر فضای یکنواخت است.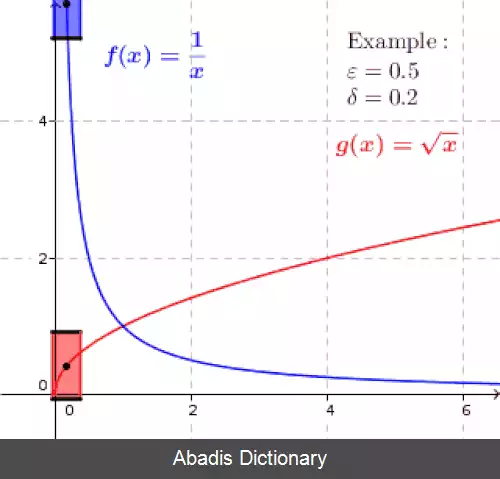
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر توابع پیوسته روی دامنه متناهی بی کران باشند ممکن است به طور یکنواخت پیوسته نباشند همچون f ( x ) = 1 x روی ( 0 , 1 ) ، یا در حالتی که شیب خطوط مماس بر تابع مورد نظر بی کران باشند همچون f ( x ) = x 2 روی خط حقیقی. با این حال، هر نگاشت لیپشیتز بین فضاهای متری به طور یکنواخت پیوسته است، بخصوص هر ایزومتری ( نگاشت حافظ فاصله ) پیوسته یکنواخت است.
گرچه که پیوستگی عادی را می توان برای توابع روی فضای توپولوژی تعریف نمود، ولی تعریف پیوستگی یکنواخت برای چنین توابعی نیازمند ساختارهای بیشتری ست. این مفهم به اندازه همسایگی های نقاط مجزا وابسته بوده، بنابراین نیازمند فضای متری یا در حالت کلی تر فضای یکنواخت است.

wiki: پیوستگی یکنواخت
