پیشامد
/piSAmad/
مترادف پیشامد: اتفاق، حادثه، رخداد، رویداد، سانحه، عارضه، ماجرا، واقعه
معنی انگلیسی:
لغت نامه دهخدا
فرهنگ فارسی
( پیش آمد ) ( صفت اسم ) حادثه قضیه رویداد سانحه عارضه .
فرهنگ معین
فرهنگ عمید
فرهنگستان زبان و ادب
{incident} [مهندسی مخابرات] رویدادهایی که به طور بالقوه یا بالفعل بر سامانۀ ارتباطی اثر منفی می گذارند
دانشنامه عمومی
در نظریه ی احتمالات ، پیشامد مجموعه ای شامل برخی نتایج ممکن برای آزمایشی تصادفی است که زیرمجموعه ای از فضای نمونه می باشد. [ ۱] اگر برآمد ( نتیجه، خروجی ) یک آزمایش در پیشامد E وجود داشته باشد می گوییم پیشامد E رخ داده است. برآمد حاصل از یک آزمایش می تواند عضو پیشامدهای متعددی باشد. [ ۲] همچنین پیشامدهای مختلفی می توانند روی یک آزمایش تعریف شوند که لزوماً احتمال وقوع آن ها یکسان نیست؛ زیرا هر کدام می توانند شامل گروه های مختلفی از برآمدها باشند.
• پیشامد اینکه مجموع اعداد ظاهر شده ی حاصل از پرتاب ۲ تاس ۶ شود:
E 1 = { ( 1 , 5 ) , ( 2 , 4 ) , ( 3 , 3 ) , ( 4 , 2 ) , ( 5 , 1 ) }
• پیشامد اینکه عمر یک ترانزیستور کمتر از ۵ساعت باشد:
E 2 = { t : 0 < = t < 5 }
• پیشامد اینکه در پرتاب ۲ سکه اولی رو بیاید:
E 3 = { ( H , H ) , ( H , T ) }
• پیشامد اینکه یک بچه دختر باشد:
E 4 = { g } زمانی که همهٔ برآمدها احتمال وقوع یکسان داشته باشند، احتمال وقوع پیشامد A ( از فضای نمونهٔ S ) از فرمول زیر به دست می آید: P ( E ) = | A | | S |
برای هر ۲پیشامد E و F پیشامد E ∪ F اجتماع E و F نامیده می شود و شامل برآمدهایی است که دست کم در یکی از پیشامدهای E و F آمده باشند. به طور مشابه می توانیم راجع به اجتماع بیش از ۲ پیشامد بحث کنیم: ⋃ i = 1 n E i همچنین پیشامد E F ( یا E ∩ F ) اشتراک E و F تعریف می شود و شامل برآمدهایی است که عضو هر ۲ پیشامد E و F باشند. ( برای n پیشامد داریم : ⋂ i = 1 n E i ) مثال: اگر پیشامد F را ۶ شدن حاصل ضرب اعداد ظاهر شده در پرتاب ۲ تاس تعریف کنیم ( F = { ( 1 , 6 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 6 , 1 ) } ) پیشامد E 1 ∩ F شامل هیچ عضوی نخواهد بود و پیشامد تهی ( E 1 ∩ F = ∅ ) نامیده می شود. [ ۳] در نهایت برای هر پیشامد E ، E c ( یا ′ E ) مکمل آن نام دارد و شامل همهٔ عضوهای فضای نمونه که در E نباشند می باشد. E c یکتا می باشد. در یک آزمایش تصادفی مجموع احتمال وقوع همهٔ برآمدها ( فضای نمونه ) برابر یک است. هر پیشامد و مکملش همهٔ اعضای فضای نمونه را شامل می شوند و هیچ عضو مشترکی ندارند بنابراین احتمال E c به صورت زیر محاسبه می شود: P ( A c ) = 1 − P ( A ) .
در نظریهٔ احتمالات یک پیشامد ساده نامیده می شود اگر تنها شامل یک عضو فضای نمونه باشد. در نظریه ی مجموعه ها پیشامد ساده یک مجموعه ی تک عضوی محسوب می شود. معمولاً برای سادگی به جای پیشامدهای ساده تنها برآمد آن ها نوشته می شود. مثال: در پرتاب متوالی ۲ سکه با فضای نمونهٔ S = { T T , T H , H T , H H } پیشامدهای { T T } ، { T H } ، { H T } ، { H H } ساده محسوب می شوند. [ ۴]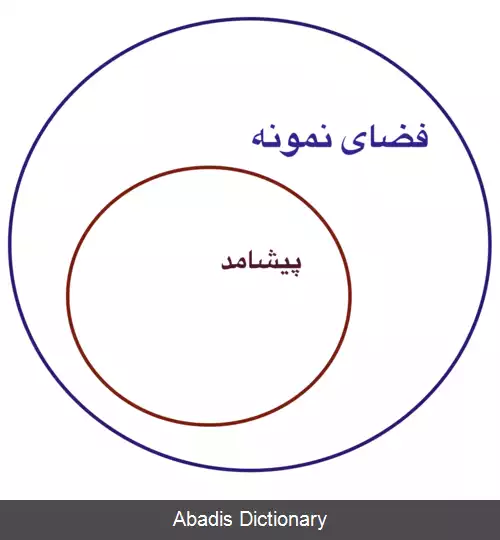
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• پیشامد اینکه مجموع اعداد ظاهر شده ی حاصل از پرتاب ۲ تاس ۶ شود:
E 1 = { ( 1 , 5 ) , ( 2 , 4 ) , ( 3 , 3 ) , ( 4 , 2 ) , ( 5 , 1 ) }
• پیشامد اینکه عمر یک ترانزیستور کمتر از ۵ساعت باشد:
E 2 = { t : 0 < = t < 5 }
• پیشامد اینکه در پرتاب ۲ سکه اولی رو بیاید:
E 3 = { ( H , H ) , ( H , T ) }
• پیشامد اینکه یک بچه دختر باشد:
E 4 = { g } زمانی که همهٔ برآمدها احتمال وقوع یکسان داشته باشند، احتمال وقوع پیشامد A ( از فضای نمونهٔ S ) از فرمول زیر به دست می آید: P ( E ) = | A | | S |
برای هر ۲پیشامد E و F پیشامد E ∪ F اجتماع E و F نامیده می شود و شامل برآمدهایی است که دست کم در یکی از پیشامدهای E و F آمده باشند. به طور مشابه می توانیم راجع به اجتماع بیش از ۲ پیشامد بحث کنیم: ⋃ i = 1 n E i همچنین پیشامد E F ( یا E ∩ F ) اشتراک E و F تعریف می شود و شامل برآمدهایی است که عضو هر ۲ پیشامد E و F باشند. ( برای n پیشامد داریم : ⋂ i = 1 n E i ) مثال: اگر پیشامد F را ۶ شدن حاصل ضرب اعداد ظاهر شده در پرتاب ۲ تاس تعریف کنیم ( F = { ( 1 , 6 ) , ( 2 , 3 ) , ( 3 , 2 ) , ( 6 , 1 ) } ) پیشامد E 1 ∩ F شامل هیچ عضوی نخواهد بود و پیشامد تهی ( E 1 ∩ F = ∅ ) نامیده می شود. [ ۳] در نهایت برای هر پیشامد E ، E c ( یا ′ E ) مکمل آن نام دارد و شامل همهٔ عضوهای فضای نمونه که در E نباشند می باشد. E c یکتا می باشد. در یک آزمایش تصادفی مجموع احتمال وقوع همهٔ برآمدها ( فضای نمونه ) برابر یک است. هر پیشامد و مکملش همهٔ اعضای فضای نمونه را شامل می شوند و هیچ عضو مشترکی ندارند بنابراین احتمال E c به صورت زیر محاسبه می شود: P ( A c ) = 1 − P ( A ) .
در نظریهٔ احتمالات یک پیشامد ساده نامیده می شود اگر تنها شامل یک عضو فضای نمونه باشد. در نظریه ی مجموعه ها پیشامد ساده یک مجموعه ی تک عضوی محسوب می شود. معمولاً برای سادگی به جای پیشامدهای ساده تنها برآمد آن ها نوشته می شود. مثال: در پرتاب متوالی ۲ سکه با فضای نمونهٔ S = { T T , T H , H T , H H } پیشامدهای { T T } ، { T H } ، { H T } ، { H H } ساده محسوب می شوند. [ ۴]

wiki: پیشامد
دانشنامه آزاد فارسی
پیشامَد (event)
در آمار، هر رویدادی که بتوان احتمالی را به آن نسبت داد. پیشامد ممکن است ساده (منفرد) باشد، مانند این که وقتی تاس می ریزیم ۶ بیاید یا آن که مرکب باشد، مانند عددهای حاصل از ریختن دو تاس. گاهی، ازجمله هنگام ریختن تاس سالم، احتمال وقوع پیشامدها یکی است.
در آمار، هر رویدادی که بتوان احتمالی را به آن نسبت داد. پیشامد ممکن است ساده (منفرد) باشد، مانند این که وقتی تاس می ریزیم ۶ بیاید یا آن که مرکب باشد، مانند عددهای حاصل از ریختن دو تاس. گاهی، ازجمله هنگام ریختن تاس سالم، احتمال وقوع پیشامدها یکی است.
wikijoo: پیشامد
مترادف ها
تصادف، حادثه، پیش امد، اصول صرف و نحو
تصادف، حادثه، پیش امد، سانحه، اتفاق، واقعه ناگوار، پا، تصادف اتومبیل، مصیبت ناگهانی، صفت، صرف، عارضه، شیی ء
حادثه، پیش امد، سانحه، اتفاق، عارضه، سرگذشت، روی داد، واقعه
پیش امد، اتفاق، پا، روی داد
پیش امد، شرح، امر، چگونگی، حال، شرایط محیط، تفصیل، اهمیت، روی داد
پیش امد، ضرورت
تصادف، پیش امد، اتفاق، روی داد، واقعه، وقوع، رخداد
فارسی به عربی
علم الصرف
پیشنهاد کاربران
معنی اثر یا پیشامد هم شاید بدهد: به عنوان اثر نمایشگاهی در پرفورمنس آرت
اتفاق، حاصل
به ترکی "اولاجاق" میگویند از مصدر "اولماق" به معنی شدن
شرح حال
نایبه ، نائبه
تصادف
حادثه
اتفاق
حادث شدن, بختامد
اتفاق که به صورت حادثه پیش بیاییدو کمترین اراده در ان سهیم باشد
