پروتکل تبادل کلید دیفی - هلمن، یک پروتکل رمزنگاری است که با استفاده از آن، دو نفر یا دو سازمان، می توانند بدون نیاز به هر گونه آشنایی قبلی، یک کلید رمز مشترک ایجاد و آن را از طریق یک مسیر ارتباطی غیر امن، بین خود تبادل نمایند. این پروتکل، اولین روش عملی مطرح شده برای تبادل کلید رمز در مسیرهای ارتباطی غیر امن است و مشکل تبادل کلید رمز در الگوریتم کلید متقارن را آسان می سازد.
این پروتکل، در سال ۱۹۷۶ توسط دو دانشمند رمزشناس به نام های ویتفیلد دیفی و مارتین هلمن طراحی شده و در قالب یک مقالهٔ علمی منتشر گردیده است. مطرح شدن این پروتکل، گام مهمی در معرفی و توسعهٔ رمزنگاری کلید عمومی یا الگوریتم نامتقارن به حساب می آید.
تا قبل از انتشار این پروتکل، رمزنگاری بیشتر به صورت رمزنگاری کلید متقارن مورد استفاده قرار می گرفته است. در سال ۱۹۷۶، با انتشار این پروتکل، پایهٔ اولیهٔ رمزنگاری کلید نامتقارن بنا شد که بعداً با فعالیت های رالف مرکل تکمیل گردید. مدتی بعد نیز الگوریتم رمز مشهور آراس ای که از مبانی مشابهی برخوردار است مطرح گردید.
در سال ۱۹۹۷، یک مؤسسه تحقیقاتی جاسوسی در انگلستان ادعا کرد که پروتکل دیفی - هِلمن، قبل از سال ۱۹۷۶ توسط فردی به نام مالکولم ویلیامسون در آن مؤسسه اختراع شده و تنها به دلایل امنیتی از انتشار آن جلوگیری شده بوده است.
در سال ۲۰۰۲، مارتین هِلمن در کتابش خاطرنشان کرد که رالف مِرکل نیز به همان اندازهٔ دیفی و هِلمن در ایجاد و گسترش رمزنگاری کلید نامتقارن تأثیرگذار بوده است و پیشنهاد کرد که این پروتکل به نام دیفی - هِلمن - مِرکل شناخته شود.
در سال های بعد از ۱۹۷۶ و با گسترش تدریجی رمزنگاری کلید نامتقارن، پروتکل های تبادل کلید مختلفی با استفاده از پروتکل دیفی - هلمن و با قابلیت های بیشتری نسبت به آن طراحی شده است.
در فرمول های پیشنهادی اولیه این پروتکل، از گروه همنهشتی اعداد صحیح با پیمانهٔ عدد اول p و عملگر ضرب اعداد صحیح استفاده شده است. در این گروه عددی، یک ریشهٔ اولیه محاسبه می شود که آن را با g نشان می دهند.
سپس مراحل زیر که در شکل روبرو هم نشان داده شده است، انجام می شود:
• مقدار عدد اول دلخواه بزرگ p ( پیمانهٔ عمل ضرب ) و مقدار محاسبه شده برای g میان دو طرف رد و بدل می شود.
• هر یک از دو طرف یک عدد صحیح دلخواه ( a و b ) را به صورت پنهانی در نظر می گیرد.
• هر یک از دو طرف با استفاده از عمل به توان رسانی پیمانه ای و مقادیر قبلی ( p و g و مقدار پنهانی ) ، یک مقدار جدید محاسبه کرده ( A و B ) و برای طرف مقابل ارسال می کند.
• طرف اول با استفاده از مقادیر p و g و a و B، و طرف دوم با استفاده از مقادیر p و g و b و A، و با همان عمل توان پیمانه ای مقدار جدیدی را محاسبه می کنند. مقدار جدید محاسبه شده - چنان که فرمول نشان می دهد - در دو طرف یکسان و همان کلید رمز مشترک است.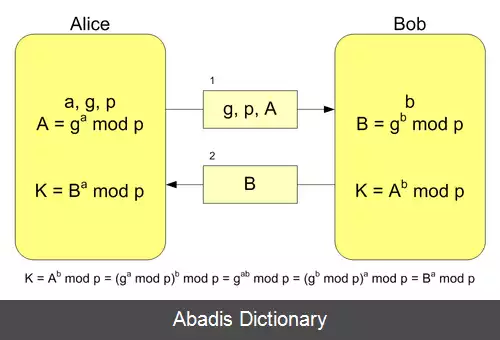
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین پروتکل، در سال ۱۹۷۶ توسط دو دانشمند رمزشناس به نام های ویتفیلد دیفی و مارتین هلمن طراحی شده و در قالب یک مقالهٔ علمی منتشر گردیده است. مطرح شدن این پروتکل، گام مهمی در معرفی و توسعهٔ رمزنگاری کلید عمومی یا الگوریتم نامتقارن به حساب می آید.
تا قبل از انتشار این پروتکل، رمزنگاری بیشتر به صورت رمزنگاری کلید متقارن مورد استفاده قرار می گرفته است. در سال ۱۹۷۶، با انتشار این پروتکل، پایهٔ اولیهٔ رمزنگاری کلید نامتقارن بنا شد که بعداً با فعالیت های رالف مرکل تکمیل گردید. مدتی بعد نیز الگوریتم رمز مشهور آراس ای که از مبانی مشابهی برخوردار است مطرح گردید.
در سال ۱۹۹۷، یک مؤسسه تحقیقاتی جاسوسی در انگلستان ادعا کرد که پروتکل دیفی - هِلمن، قبل از سال ۱۹۷۶ توسط فردی به نام مالکولم ویلیامسون در آن مؤسسه اختراع شده و تنها به دلایل امنیتی از انتشار آن جلوگیری شده بوده است.
در سال ۲۰۰۲، مارتین هِلمن در کتابش خاطرنشان کرد که رالف مِرکل نیز به همان اندازهٔ دیفی و هِلمن در ایجاد و گسترش رمزنگاری کلید نامتقارن تأثیرگذار بوده است و پیشنهاد کرد که این پروتکل به نام دیفی - هِلمن - مِرکل شناخته شود.
در سال های بعد از ۱۹۷۶ و با گسترش تدریجی رمزنگاری کلید نامتقارن، پروتکل های تبادل کلید مختلفی با استفاده از پروتکل دیفی - هلمن و با قابلیت های بیشتری نسبت به آن طراحی شده است.
در فرمول های پیشنهادی اولیه این پروتکل، از گروه همنهشتی اعداد صحیح با پیمانهٔ عدد اول p و عملگر ضرب اعداد صحیح استفاده شده است. در این گروه عددی، یک ریشهٔ اولیه محاسبه می شود که آن را با g نشان می دهند.
سپس مراحل زیر که در شکل روبرو هم نشان داده شده است، انجام می شود:
• مقدار عدد اول دلخواه بزرگ p ( پیمانهٔ عمل ضرب ) و مقدار محاسبه شده برای g میان دو طرف رد و بدل می شود.
• هر یک از دو طرف یک عدد صحیح دلخواه ( a و b ) را به صورت پنهانی در نظر می گیرد.
• هر یک از دو طرف با استفاده از عمل به توان رسانی پیمانه ای و مقادیر قبلی ( p و g و مقدار پنهانی ) ، یک مقدار جدید محاسبه کرده ( A و B ) و برای طرف مقابل ارسال می کند.
• طرف اول با استفاده از مقادیر p و g و a و B، و طرف دوم با استفاده از مقادیر p و g و b و A، و با همان عمل توان پیمانه ای مقدار جدیدی را محاسبه می کنند. مقدار جدید محاسبه شده - چنان که فرمول نشان می دهد - در دو طرف یکسان و همان کلید رمز مشترک است.

