ولگشت خودپرهیز (قدم زدن بدون قطع کردن خود). الگو:شبیه سازی مونت کارلو {{[ ۱] |تاریخ=دسامبر ۲۰۱۸}}
در ریاضیات، ولگشت خود پرهیز یا قدم زدن بدون قطع کردن خود ( به انگلیسی: Self Avoiding Walk یا SAW ) به توالی ای از حرکات در توری می گویند که از یک نقطه بیش از یک بار عبور نکند. این حالت یکی از حالات نظریه گراف از مسیر ( نظریه گراف ) است. از دیدگاه ریاضیات به سختی می توان اطلاعاتی دربارهٔ ولگشت خودپرهیز بدست آورد در حالی که فیزیکدان ها موفق شده اند تعداد زیادی تخمین بدست آورند. این تخمین ها با توجه به شبیه سازی های عددی، به نظر تا حد خوبی قابل قبول هستند.
در فیزیک محاسباتی، ولگشت خودپرهیز، مسیر زنجیر مانندی در R 2 و R 3 با تعداد مشخصی از نقاط و طول معمولاً مشخص است که مقید شده است که خودش یا ولگشت دیگری را قطع نکند. یک سیستم ولگشت خودپرهیز شرایط حجم مستثنی را ارضا می کند. پیش بینی می شود که در ابعاد بالاتر، ولگشت خودپرهیز بیشتر شبیه به ولگشت ساده رفتار کند. ولگشت خودپرهیز و چند ضلعی خودپرهیز نقشی اساسی در مدل کردن توپولوژیکال و رفتار نظریه گره مولکول های خطی و حلقوی شکل بازی می کنند. ولگشت های خودپرهیز فراکتال هستند.
خصوصیات ولگشت های خودپرهیز را نمی توان از محاسبات تحلیلی بدست آورد، بنابراین برای این امر از شبیه سازی های عددی استفاده می شود. الگوریتم پیووت روشی مرسوم برای شبیه سازی زنجیره مارکوف مونت کارلو برای اندازه گیری یکنواخت یک ولگشت خودپرهیز با طول n است. محاسبهٔ تعداد گام های خودپرهیز در یک شبکهٔ مشخص یکی از مسائل محاسباتی مرسوم است. اگرچه هیچ فرمولی شناخته شده ای برای محاسبهٔ تعداد گام های خودپرهیز وجود ندارد، اما روش هایی برای تخمین آن وجود دارد. حدس زده می شود که تعداد این مسیرها یک مسئلهٔ ان پی سخت باشد. در یک شبکهٔ m × n برای رسیدن از یک گوشه به گوشهٔ مقابل، تعداد:
( m + n m , n )
مسیر وجود دارد.
ولگشت های خودپرهیز گاهی برای مدل کردن پلیمرهای خطی استفاده می شوند. پلیمرهای خطی، مولکول هایی هستند که از واحدهای ساده ای به نام مونومر ها به صورت زنجیری تشکیل می شوند. این زنجیره ها می توانند خیلی طولانی شوند بطوریکه گاهی بعضی از آن ها شامل 10 5 مونومر می شوند. یکی از سوالاتی که برای محققان حوزهٔ پلیمر مهم است، این است که یک زنجیر n - مونومری چند ساختار مختلف می تواند به خود بگیرد و همچنین نقطهٔ پایانی در چه فاصله ای از نقطهٔ شروع قرار دارد. این سؤال ها را می توان به زبان ولگشت های خودپرهیز ترجمه کرد و پلیمرها را همان ولگشت های خودپرهیزی در نظر گرفت که هر گام برابر یک مونومر باشد و محدودیت خودپرهیزی، حجم مستثنی را مدل می کند: «هیچ دو مونومری نمی توانند یک نقطه از فضا را اشغال کنند. »
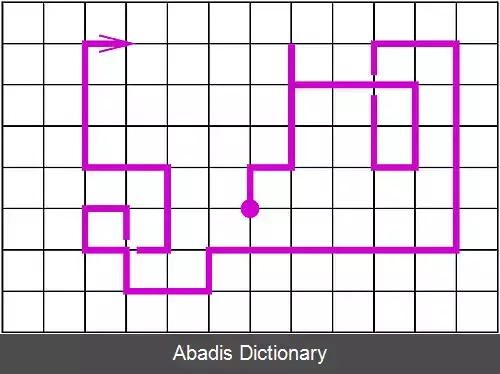
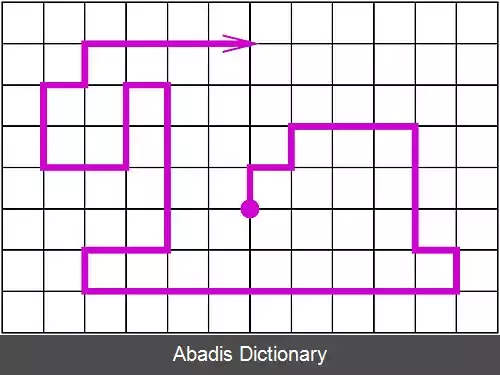
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر ریاضیات، ولگشت خود پرهیز یا قدم زدن بدون قطع کردن خود ( به انگلیسی: Self Avoiding Walk یا SAW ) به توالی ای از حرکات در توری می گویند که از یک نقطه بیش از یک بار عبور نکند. این حالت یکی از حالات نظریه گراف از مسیر ( نظریه گراف ) است. از دیدگاه ریاضیات به سختی می توان اطلاعاتی دربارهٔ ولگشت خودپرهیز بدست آورد در حالی که فیزیکدان ها موفق شده اند تعداد زیادی تخمین بدست آورند. این تخمین ها با توجه به شبیه سازی های عددی، به نظر تا حد خوبی قابل قبول هستند.
در فیزیک محاسباتی، ولگشت خودپرهیز، مسیر زنجیر مانندی در R 2 و R 3 با تعداد مشخصی از نقاط و طول معمولاً مشخص است که مقید شده است که خودش یا ولگشت دیگری را قطع نکند. یک سیستم ولگشت خودپرهیز شرایط حجم مستثنی را ارضا می کند. پیش بینی می شود که در ابعاد بالاتر، ولگشت خودپرهیز بیشتر شبیه به ولگشت ساده رفتار کند. ولگشت خودپرهیز و چند ضلعی خودپرهیز نقشی اساسی در مدل کردن توپولوژیکال و رفتار نظریه گره مولکول های خطی و حلقوی شکل بازی می کنند. ولگشت های خودپرهیز فراکتال هستند.
خصوصیات ولگشت های خودپرهیز را نمی توان از محاسبات تحلیلی بدست آورد، بنابراین برای این امر از شبیه سازی های عددی استفاده می شود. الگوریتم پیووت روشی مرسوم برای شبیه سازی زنجیره مارکوف مونت کارلو برای اندازه گیری یکنواخت یک ولگشت خودپرهیز با طول n است. محاسبهٔ تعداد گام های خودپرهیز در یک شبکهٔ مشخص یکی از مسائل محاسباتی مرسوم است. اگرچه هیچ فرمولی شناخته شده ای برای محاسبهٔ تعداد گام های خودپرهیز وجود ندارد، اما روش هایی برای تخمین آن وجود دارد. حدس زده می شود که تعداد این مسیرها یک مسئلهٔ ان پی سخت باشد. در یک شبکهٔ m × n برای رسیدن از یک گوشه به گوشهٔ مقابل، تعداد:
( m + n m , n )
مسیر وجود دارد.
ولگشت های خودپرهیز گاهی برای مدل کردن پلیمرهای خطی استفاده می شوند. پلیمرهای خطی، مولکول هایی هستند که از واحدهای ساده ای به نام مونومر ها به صورت زنجیری تشکیل می شوند. این زنجیره ها می توانند خیلی طولانی شوند بطوریکه گاهی بعضی از آن ها شامل 10 5 مونومر می شوند. یکی از سوالاتی که برای محققان حوزهٔ پلیمر مهم است، این است که یک زنجیر n - مونومری چند ساختار مختلف می تواند به خود بگیرد و همچنین نقطهٔ پایانی در چه فاصله ای از نقطهٔ شروع قرار دارد. این سؤال ها را می توان به زبان ولگشت های خودپرهیز ترجمه کرد و پلیمرها را همان ولگشت های خودپرهیزی در نظر گرفت که هر گام برابر یک مونومر باشد و محدودیت خودپرهیزی، حجم مستثنی را مدل می کند: «هیچ دو مونومری نمی توانند یک نقطه از فضا را اشغال کنند. »



