هندسه هُذلولوی یکی از هندسه های نااقلیدسی است که به هندسه لباچفسکی نیز مشهور است.
نام انگلیسی این نوع هندسه، یعنی ( Hyperbolic ) ، از کلمهٔ یونانی هیپربالئین به معنی «افزایش یافتن» گرفته شده است که در آن فاصلهٔ میان نیم خط ها در اصل توازی افزایش می یابد.
هدف از ابداع هندسه هذلولوی پیدا کردن مدل هندسی ای بود که در آن برای هر نقطه p و هر خط L تعداد نامتناهی خط گذرنده از p و عمود به L موجود باشد. در بعد دو مدلهای اساسی هندسه هذلولوی عبارتند از دیسک پوانکاره و نیم صفحه بالا.
سازگاری هندسه هذلولوی، استقلال منطقی اصل توازی را از سایر اصول هندسه اقلیدسی نشان می دهد.
در این مدل هندسه هذلولوی کوتاهترین مسیرها ( ژئودزیک ها ) عبارتند از خطهای عمودی و نیم دایره های عمود بر محور x . در هندسه ریمانی چنین هندسه با متریک ریمانی زیر به دست می آید.
d x 2 + d y 2 y 2
انحنای این متریک ثابت و برابر 1 - می باشد.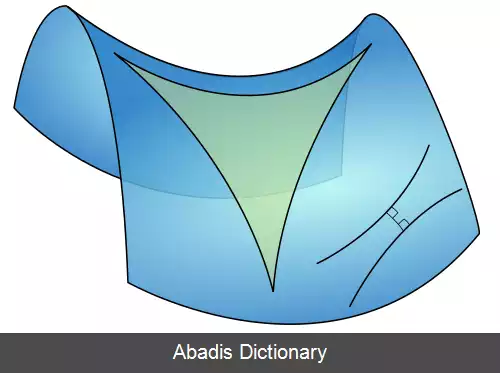

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنام انگلیسی این نوع هندسه، یعنی ( Hyperbolic ) ، از کلمهٔ یونانی هیپربالئین به معنی «افزایش یافتن» گرفته شده است که در آن فاصلهٔ میان نیم خط ها در اصل توازی افزایش می یابد.
هدف از ابداع هندسه هذلولوی پیدا کردن مدل هندسی ای بود که در آن برای هر نقطه p و هر خط L تعداد نامتناهی خط گذرنده از p و عمود به L موجود باشد. در بعد دو مدلهای اساسی هندسه هذلولوی عبارتند از دیسک پوانکاره و نیم صفحه بالا.
سازگاری هندسه هذلولوی، استقلال منطقی اصل توازی را از سایر اصول هندسه اقلیدسی نشان می دهد.
در این مدل هندسه هذلولوی کوتاهترین مسیرها ( ژئودزیک ها ) عبارتند از خطهای عمودی و نیم دایره های عمود بر محور x . در هندسه ریمانی چنین هندسه با متریک ریمانی زیر به دست می آید.
d x 2 + d y 2 y 2
انحنای این متریک ثابت و برابر 1 - می باشد.


wiki: هندسه هذلولوی
