هم گشت
لغت نامه دهخدا
فرهنگ فارسی
فرهنگستان زبان و ادب
دانشنامه عمومی
هَم گَشت[ ۱] یا کانوُلوشِن ( به انگلیسی: Convolution ) در ریاضیات یا به طور دقیق تر آنالیز تابعی، یک عملگر ریاضی است که بر روی دو تابع f و g عمل می کند. هم گشت مشابه تابع هم بستگی است. کاربردهای این عملگر شامل آمار، بینایی رایانه ای، پردازش تصویر، پردازش سیگنال، مهندسی برق و معادلات دیفرانسیل می شود. به هم گشت، هم آمیخت و پیچیدگی هم گفته شده است.
هم گشت را می توان برای توابعی از گروه های غیر از فضای اقلیدسی تعریف کرد. در حالت خاص، هم گشت دوره ای ( Cyclic Convolution ) را می توان برای توابع متناوب تعریف کرد، و هم گشت گسسته را می توان برای توابع صحیح تعریف کرد. چنین تعمیم هایی از هم گشت دارای کاربردهایی در زمینه تحلیل عددی، جبر خطی عددی، و پردازش سیگنال های گسسته دارند.
عمل
به ازای
0 ≤ t < ∞ ،
حالت خاص ضرب ترکیبی است که ریاضیدان ایتالیایی ویتو ولترا آن را مطرح کرده است. [ ۲]
هم گشت اصولاً به نام "Faltung" ( که همان Folding انگلیسی به معنی تا کردن است ) ، توسط یک ریاضیدان آلمانی به نام گوستاو دوچ معرفی شد. [ ۳]
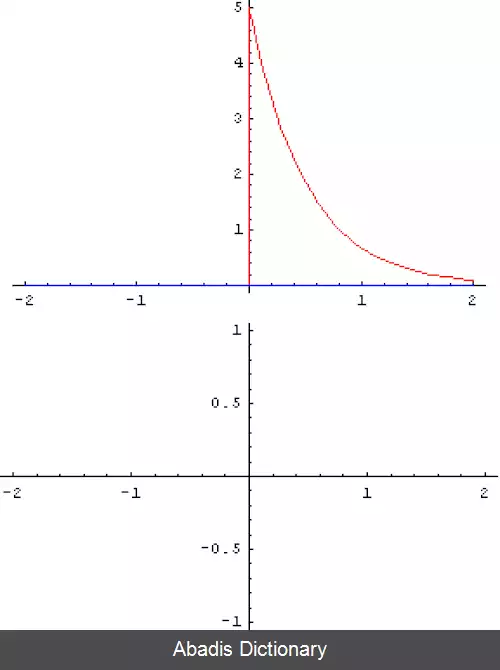
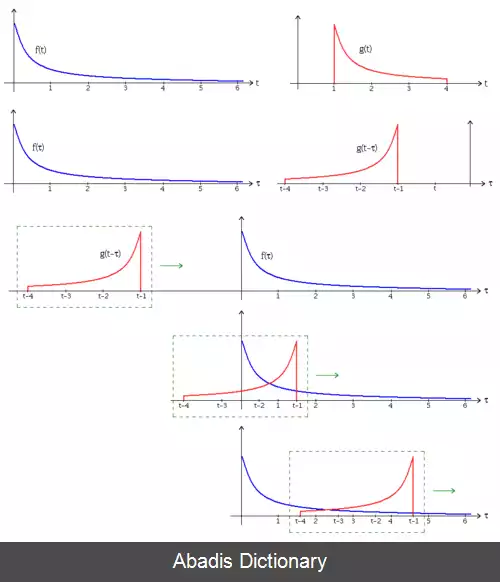
هم گشت دو تابع ƒ و g به صورت f ∗ g نوشته می شود. این تعریف به صورت انتگرال حاصلضرب دو تابع که یکی از آن ها نسبت به محور عمودی مختصات برعکس شده و روی آن یکی می لغزد تعریف می شود. با این تعریف، هم گشت یک نوع خاص از تبدیل انتگرالی است.
هم گشت را می توان به عنوان میانگین وزنی تابع ( ƒ ( τ با مومنتوم t در نظر بگیریم که وزن ها توسط ( g ( −τ به اندازه t جابجا می شوند ( لغزش می کنند ) . با تغییر t، تابع وزنی قسمت های مختلف تابع ورودی را برجسته می کند. به طور کلی، اگر f و g بر روی Rd توابع با مقدار مختلط باشند، آنگاه هم گشت را می توان به صورت انتگرال زیر تعریف کرد:
وقتی یک تابع gT متناوب باشد ( که T دوره تناوب آن است ) ، آنگاه برای تابع ƒ ( به طوری که ƒ∗gT وجود داشته باشد ) ، هم گشت نیز متناوب و یکتا خواهد بود:
که to یک مقدار انتخاب است. جمع، یک بسط متناوب از تابع ƒ خوانده می شود.
اگر gT بسط متناوب یک تابع دیگر ( مثلاً g ) باشد، آنگاه رابطه ƒ∗gT را هم گشتِ دوره ای ƒ و g می نامند.
هم گشت برای دو تابع گسسته ƒ، g که بر روی مجموعه اعداد صحیح Z تعریف شده است، انتگرال گسسته ƒ و g با رابطه زیر بدست می آید:
زمانی که دو چندجمله ای را ضرب می کنیم، ضرایب حاصلضرب توسط هم گشت توالی ضرایب اصلی بدست می آید، که برای جلوگیری از ایجاد جمله های تعریف نشده با عدد صفر بسط داده می شوند؛ این عمل تحت عنوان حاصلضرب کوشی ضرایب دو چند جمله ای شناخته می شود.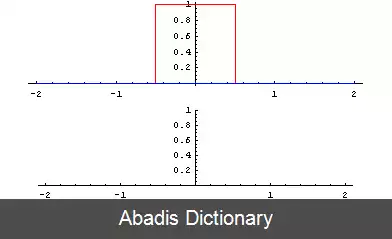
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهم گشت را می توان برای توابعی از گروه های غیر از فضای اقلیدسی تعریف کرد. در حالت خاص، هم گشت دوره ای ( Cyclic Convolution ) را می توان برای توابع متناوب تعریف کرد، و هم گشت گسسته را می توان برای توابع صحیح تعریف کرد. چنین تعمیم هایی از هم گشت دارای کاربردهایی در زمینه تحلیل عددی، جبر خطی عددی، و پردازش سیگنال های گسسته دارند.
عمل
به ازای
0 ≤ t < ∞ ،
حالت خاص ضرب ترکیبی است که ریاضیدان ایتالیایی ویتو ولترا آن را مطرح کرده است. [ ۲]
هم گشت اصولاً به نام "Faltung" ( که همان Folding انگلیسی به معنی تا کردن است ) ، توسط یک ریاضیدان آلمانی به نام گوستاو دوچ معرفی شد. [ ۳]
هم گشت دو تابع ƒ و g به صورت f ∗ g نوشته می شود. این تعریف به صورت انتگرال حاصلضرب دو تابع که یکی از آن ها نسبت به محور عمودی مختصات برعکس شده و روی آن یکی می لغزد تعریف می شود. با این تعریف، هم گشت یک نوع خاص از تبدیل انتگرالی است.
هم گشت را می توان به عنوان میانگین وزنی تابع ( ƒ ( τ با مومنتوم t در نظر بگیریم که وزن ها توسط ( g ( −τ به اندازه t جابجا می شوند ( لغزش می کنند ) . با تغییر t، تابع وزنی قسمت های مختلف تابع ورودی را برجسته می کند. به طور کلی، اگر f و g بر روی Rd توابع با مقدار مختلط باشند، آنگاه هم گشت را می توان به صورت انتگرال زیر تعریف کرد:
وقتی یک تابع gT متناوب باشد ( که T دوره تناوب آن است ) ، آنگاه برای تابع ƒ ( به طوری که ƒ∗gT وجود داشته باشد ) ، هم گشت نیز متناوب و یکتا خواهد بود:
که to یک مقدار انتخاب است. جمع، یک بسط متناوب از تابع ƒ خوانده می شود.
اگر gT بسط متناوب یک تابع دیگر ( مثلاً g ) باشد، آنگاه رابطه ƒ∗gT را هم گشتِ دوره ای ƒ و g می نامند.
هم گشت برای دو تابع گسسته ƒ، g که بر روی مجموعه اعداد صحیح Z تعریف شده است، انتگرال گسسته ƒ و g با رابطه زیر بدست می آید:
زمانی که دو چندجمله ای را ضرب می کنیم، ضرایب حاصلضرب توسط هم گشت توالی ضرایب اصلی بدست می آید، که برای جلوگیری از ایجاد جمله های تعریف نشده با عدد صفر بسط داده می شوند؛ این عمل تحت عنوان حاصلضرب کوشی ضرایب دو چند جمله ای شناخته می شود.



wiki: هم گشت
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
