فرهنگستان زبان و ادب
دانشنامه عمومی
هم نهشتی (نظریه اعداد). نظریۀ هم نهشتی یا حساب پیمانه ای ( به انگلیسی: modular arithmetic ) سیستمی برای محاسبه با اعداد صحیح است که به وسیله کارل فردریش گاوس در کتاب رسالۀ حساب در سال ۱۸۰۱ معرفی شد.
مفهوم هم نهشتی را می توان به عنوان پالایشی برای نظریۀ بخش پذیری دانست و به وسیلۀ آن می توان مفاهیم بنیادی را در نظریۀ اعداد مورد مطالعه قرار داد که بدون استفاده از آن، بیان و اثبات بسیاری از مطالب در نظریۀ اعداد دشوار یا غیرممکن خواهد بود. به علاوه هم نهشتی ها می توانند خیلی شبیه به معادلات مورد بحث قرار بگیرند و از این رو رابطه ای شبیه به تساوی ایجاد خواهند کرد.
به همین دلیل، گاوس نماد ≡ را برای هم نهشتی معرفی نمود. یکی از کاربردهای مهم هم نهشتی ها در حل معادلات سیاله است. مفهوم هم نهشتی در موارد بسیاری در زندگی ما مشهود است. یکی از کاربردهای آشنای هم نهشتی ها در زندگی روزمره، استفاده از ۲۴ ساعت در شبانه روز است. به طور کلی هر پدیده ای که به صورت دوره ای رخ می دهد، بیانگر کاربردی از هم نهشتی است.
• قرار داد: از این پس حروف m {\displaystyle m} و n {\displaystyle n} بیانگر اعداد طبیعی و حروف a , b , c , . . . {\displaystyle a, b, c, . . . } ، بیانگر اعداد صحیح خواهند بود. مگر آنکه خلاف آن صریحاً تصریح شود.
گوئیم عدد a به پیمانۀ ( سنج ) m با b هم نهشت است و می نویسیم:
از آنجا که با توجه به این تعریف هر دو عدد طبیعی به پیمانه m = 1 با هم هم نهشت می باشند، پیمانه را معمولاً عدد طبیعی بزرگ تر از یک در نظر می گیریم. به علاوه برای سهولت در نوشتار، گاهی نماد a ≡ m b را برای نمایش هم نهشتی به پیمانۀ m استفاده می کنیم.
اگر a و b به پیمانۀ m هم نهشت نباشد، می نویسیم: a ≢ b ( mod m ) .
به عنوان مثال: 30 ≡ 9 ( mod 7 ) چرا که 7 | 30 − 9 ولی 30 ≢ 12 ( mod 7 ) . وقتی می گوئیم a ، m را عاد می کند، یعنی: m = a k .
هم نهشتی به پیمانۀ دلخواه m ، یک رابطه را روی مجموعۀ اعداد صحیح تعریف می کند. این رابطه را به صورت ≡ m نشان می دهیم و برای هر دو عدد صحیح a , b به صورت:
تعریف می کنیم.
با کمی دقت متوجه می شویم که این رابطه یک رابطه هم ارزی روی مجموعۀ اعداد صحیح است.
• برای هر عدد صحیح a داریم m|a - a پس a ≡ m a {\displaystyle a\equiv _{m}a} ولذا رابطه ≡ m {\displaystyle \equiv _{m}} منعکس است.
• برای هر دو عدد صحیح a, b اگر a ≡ m b {\displaystyle a\equiv _{m}b} آنگاه بنابه تعریف m|a - b پس m|b - a و در نتیجه b ≡ m a {\displaystyle b\equiv _{m}a} و لذا رابطه ≡ m {\displaystyle \equiv _{m}} متقارن است.
• برای هر سه عدد صحیح a, b, c اگر a ≡ m b {\displaystyle a\equiv _{m}b} و b ≡ m c {\displaystyle b\equiv _{m}c} آنگاه m|a - b و m|b - c حال با توجه به خواص رابطه عاد کردن می توان نوشت m|a - c پس a ≡ m c {\displaystyle a\equiv _{m}c} و لذا رابطه ≡ m {\displaystyle \equiv _{m}} متعدی است.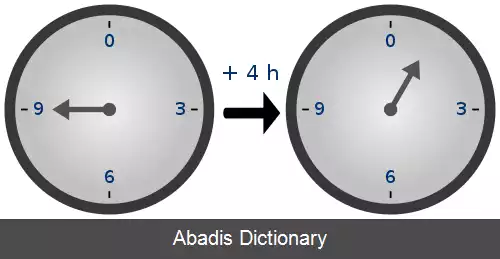
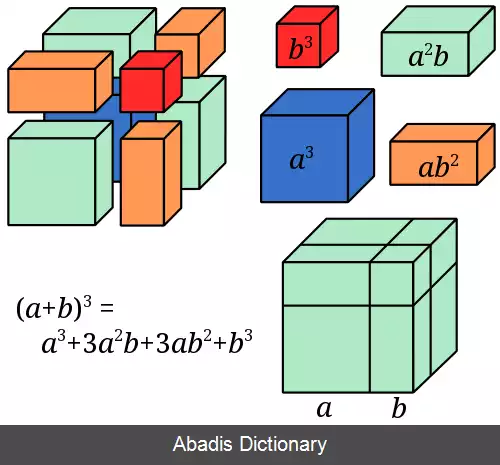
مفهوم هم نهشتی را می توان به عنوان پالایشی برای نظریۀ بخش پذیری دانست و به وسیلۀ آن می توان مفاهیم بنیادی را در نظریۀ اعداد مورد مطالعه قرار داد که بدون استفاده از آن، بیان و اثبات بسیاری از مطالب در نظریۀ اعداد دشوار یا غیرممکن خواهد بود. به علاوه هم نهشتی ها می توانند خیلی شبیه به معادلات مورد بحث قرار بگیرند و از این رو رابطه ای شبیه به تساوی ایجاد خواهند کرد.
به همین دلیل، گاوس نماد ≡ را برای هم نهشتی معرفی نمود. یکی از کاربردهای مهم هم نهشتی ها در حل معادلات سیاله است. مفهوم هم نهشتی در موارد بسیاری در زندگی ما مشهود است. یکی از کاربردهای آشنای هم نهشتی ها در زندگی روزمره، استفاده از ۲۴ ساعت در شبانه روز است. به طور کلی هر پدیده ای که به صورت دوره ای رخ می دهد، بیانگر کاربردی از هم نهشتی است.
• قرار داد: از این پس حروف m {\displaystyle m} و n {\displaystyle n} بیانگر اعداد طبیعی و حروف a , b , c , . . . {\displaystyle a, b, c, . . . } ، بیانگر اعداد صحیح خواهند بود. مگر آنکه خلاف آن صریحاً تصریح شود.
گوئیم عدد a به پیمانۀ ( سنج ) m با b هم نهشت است و می نویسیم:
از آنجا که با توجه به این تعریف هر دو عدد طبیعی به پیمانه m = 1 با هم هم نهشت می باشند، پیمانه را معمولاً عدد طبیعی بزرگ تر از یک در نظر می گیریم. به علاوه برای سهولت در نوشتار، گاهی نماد a ≡ m b را برای نمایش هم نهشتی به پیمانۀ m استفاده می کنیم.
اگر a و b به پیمانۀ m هم نهشت نباشد، می نویسیم: a ≢ b ( mod m ) .
به عنوان مثال: 30 ≡ 9 ( mod 7 ) چرا که 7 | 30 − 9 ولی 30 ≢ 12 ( mod 7 ) . وقتی می گوئیم a ، m را عاد می کند، یعنی: m = a k .
هم نهشتی به پیمانۀ دلخواه m ، یک رابطه را روی مجموعۀ اعداد صحیح تعریف می کند. این رابطه را به صورت ≡ m نشان می دهیم و برای هر دو عدد صحیح a , b به صورت:
تعریف می کنیم.
با کمی دقت متوجه می شویم که این رابطه یک رابطه هم ارزی روی مجموعۀ اعداد صحیح است.
• برای هر عدد صحیح a داریم m|a - a پس a ≡ m a {\displaystyle a\equiv _{m}a} ولذا رابطه ≡ m {\displaystyle \equiv _{m}} منعکس است.
• برای هر دو عدد صحیح a, b اگر a ≡ m b {\displaystyle a\equiv _{m}b} آنگاه بنابه تعریف m|a - b پس m|b - a و در نتیجه b ≡ m a {\displaystyle b\equiv _{m}a} و لذا رابطه ≡ m {\displaystyle \equiv _{m}} متقارن است.
• برای هر سه عدد صحیح a, b, c اگر a ≡ m b {\displaystyle a\equiv _{m}b} و b ≡ m c {\displaystyle b\equiv _{m}c} آنگاه m|a - b و m|b - c حال با توجه به خواص رابطه عاد کردن می توان نوشت m|a - c پس a ≡ m c {\displaystyle a\equiv _{m}c} و لذا رابطه ≡ m {\displaystyle \equiv _{m}} متعدی است.


wiki: هم نهشتی (نظریه اعداد)
هم نهشتی (هندسه). در هندسه دو شکل هم نهشت هستند اگر بتوان با صد تبدیل ( ترکیبی از انتقال، دوران و بازتاب ) آن ها را برهم منطبق کرد؛ به عبارت دیگر، در دو شکل، تمامی زوایا و اضلاع نظیر هم برابر باشند. اگر دو شکل هم نهشت باشند، تمام اجزای آن ها نیز هم نهشت ( برابر، مساوی ) هستند. [ ۱]
• دو زاویه و ضلع ( ز. ض. ز ) :دو مثلث هم نهشت اند اگر اندازه یک ضلع یکی از آنها برابر اندازه ضلع نظیرش از مثلث دیگر و دو زاویه آنها برابر دو زاویه نظیرشان از مثلث دیگر باشد.
• دو ضلع و زاویه ی بین ( ض. ز. ض ) :دو مثلث هم نهشت اند اگر اندازه ی دو ضلع یک مثلث برابر اندازه ضلع های نظیرشان از مثلث دیگر و زاویه های بین این ضلع ها برابر باشند.
• سه ضلع ( ض. ض. ض ) :دو مثلث هم نهشت اند اگر طول های سه ضلع از یک مثلث برابر طول ضلع های نظیرشان از مثلث دیگری باشند.
• سه زاویه ( ز. ز. ز ) :دو مثلث هم نهشت اند اگر اندازه سه زاویه از یک مثلث برابر اندازه زاویه های نظیرشان از مثلث دیگری باشند.
• اگر مثلث متساوی الساقین باشد دو حالت دیگر اضافه می شود: ( این دو حالت فقط در حالتی صدق می کنند که مثلث مورد نظر متساوی الساقین باشد. )
• ساق و قاعده ( س. ق )
• ضلع و زاویه ( ض. ز )
• اگر مثلث قائم الزاویه باشد سه حالت دیگر اضافه می شود: ( این سه حالت فقط در حالتی صدق می کنند که مثلث مورد نظر قائم الزاویه باشد. )
• ضلع و زاویه ی حاده ( ض. ز )
• دو ضلع ( ض. ض )
• ضلع و ارتفاع وارد بر وتر ( ض. ا )
اجزای متناظر دو شکل هم نهشت کاملاً با هم برابر هستند. ( زاویه ها و ضلعهای متناظر با هم برابرند )
نکته: میتوان همه شکلها را به کمک تبدیل های هندسی برهم منطبق کرد و پوشاند.
نکته: تمام شکل های هم نهشت را می توان با کمک سه تبدیل هندسی دوران و انتقال و تقارن بر هم منطبق کرد.
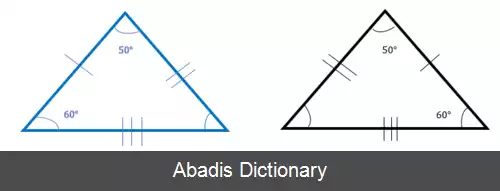
در شکل زیر ، دو مثلث را میبینیم که زوایا و ضلع های برابری دارند.
پس ویژگی اصلی این است که اندازه زاویه ها و ضلع ها با هم برابر باشند
دو نکته را می توان با استفاده از مثلث های همنهشت فهمید.
• هر نقطه روی عمودمُنَصّف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
• هر نقطه روی نیمساز یک زاویه از دو ضلع زاویه به یک فاصله است.
↑ مثلث های هم نهشت «سیده فاطمه موسوی نطنزی»
• مقاله های خرد هندسه
• مثلث ها
• هم ارزی
• هندسه اقلیدسی
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• دو زاویه و ضلع ( ز. ض. ز ) :دو مثلث هم نهشت اند اگر اندازه یک ضلع یکی از آنها برابر اندازه ضلع نظیرش از مثلث دیگر و دو زاویه آنها برابر دو زاویه نظیرشان از مثلث دیگر باشد.
• دو ضلع و زاویه ی بین ( ض. ز. ض ) :دو مثلث هم نهشت اند اگر اندازه ی دو ضلع یک مثلث برابر اندازه ضلع های نظیرشان از مثلث دیگر و زاویه های بین این ضلع ها برابر باشند.
• سه ضلع ( ض. ض. ض ) :دو مثلث هم نهشت اند اگر طول های سه ضلع از یک مثلث برابر طول ضلع های نظیرشان از مثلث دیگری باشند.
• سه زاویه ( ز. ز. ز ) :دو مثلث هم نهشت اند اگر اندازه سه زاویه از یک مثلث برابر اندازه زاویه های نظیرشان از مثلث دیگری باشند.
• اگر مثلث متساوی الساقین باشد دو حالت دیگر اضافه می شود: ( این دو حالت فقط در حالتی صدق می کنند که مثلث مورد نظر متساوی الساقین باشد. )
• ساق و قاعده ( س. ق )
• ضلع و زاویه ( ض. ز )
• اگر مثلث قائم الزاویه باشد سه حالت دیگر اضافه می شود: ( این سه حالت فقط در حالتی صدق می کنند که مثلث مورد نظر قائم الزاویه باشد. )
• ضلع و زاویه ی حاده ( ض. ز )
• دو ضلع ( ض. ض )
• ضلع و ارتفاع وارد بر وتر ( ض. ا )
اجزای متناظر دو شکل هم نهشت کاملاً با هم برابر هستند. ( زاویه ها و ضلعهای متناظر با هم برابرند )
نکته: میتوان همه شکلها را به کمک تبدیل های هندسی برهم منطبق کرد و پوشاند.
نکته: تمام شکل های هم نهشت را می توان با کمک سه تبدیل هندسی دوران و انتقال و تقارن بر هم منطبق کرد.
در شکل زیر ، دو مثلث را میبینیم که زوایا و ضلع های برابری دارند.
پس ویژگی اصلی این است که اندازه زاویه ها و ضلع ها با هم برابر باشند
دو نکته را می توان با استفاده از مثلث های همنهشت فهمید.
• هر نقطه روی عمودمُنَصّف یک پاره خط از دو سر آن پاره خط به یک فاصله است.
• هر نقطه روی نیمساز یک زاویه از دو ضلع زاویه به یک فاصله است.
↑ مثلث های هم نهشت «سیده فاطمه موسوی نطنزی»
• مقاله های خرد هندسه
• مثلث ها
• هم ارزی
• هندسه اقلیدسی



wiki: هم نهشتی (هندسه)
پیشنهاد کاربران
همنهشتی یعنی تطابق، مثلا دو مثلث که هر سه ضلع آن دو با هم مساوی باشند، آن دو مثلث برهم منطبق خواهند بود و باهم تطابق دارند.
تطابق
