در هندسه، هفده ضلعی ( به انگلیسی: Heptadecagon ) ، یک چندضلعی با هفده ضلع است.
یک هفده ضلعی منتظم دارای ضلع ها و زاویه های داخلی برابر است. اندازهٔ زاویه های داخلی هر رأس آن، حدود ۱۵۸٫۸ درجه بوده و مساحت آن با استفاده از رابطهٔ زیر محاسبه می شود:
یک هفده ضلعی منتظم با استفاده از خط کش غیرمدرج و پرگار قابل ترسیم است. این موضوع در سال ۱۷۹۶ توسط کارل فریدریش گاوس ۱۹ ساله اثبات شد. [ ۲] این اثبات، نخستین پیشرفت در ترسیم چندضلعی های منتظم پس از بیش از ۲۰۰۰ سال بود. [ ۲]
اثبات گاوس، بر اساس این حقیقت بود که اولاً قابل ترسیم بودن، معادل است با قابل بیان بودن تابع های مثلثاتی زاویهٔ مشترک بر اساس عمل گرهای حسابی و ریشه دوم، و دوم اینکه این کار قابل انجام است اگر توان های اول فرد n اعداد اول فرمای متفاوتی ( به فرم F n = 2 2 n + 1 ) باشند.
بنابراین، ترسیم یک هفده ضلعی منتظم، شامل یافتن کسینوس 2 π / 17 بر حسب ریشه دوم است. گاوس در کتاب بررسی های حسابی ( Disquisitiones Arithmeticae ) خود، این رابطه را به این صورت استخراج کرده است:
ترسیم چندضلعی های منتظم با 2h ضلع، توسط اقلیدس شناخته شده بود، ولی ترسیم بر اساس اعداد فرما ( به جز ۳ و ۵ ) در ریاضیات باستان ناشناخته بود.
نخستین ترسیم صریح از هفده ضلعی در سال ۱۸۲۵ توسط یوهان ارشینگر انجام گرفت. یک روش دیگر بر اساس استفاده از دایره های کارلایل به صورت زیر است. بر اساس ترسیم یک هفده ضلعی منتظم، می توان به راحتی n - ضلعی هایی با n به صورت حاصل ضرب ۱۷ در ۳ یا ۵ ( و یا هر دو ) و هر توان ۲ ( مثلاً ۵۱ - ضلعی، ۸۵ - ضلعی، یا ۲۵۵ - ضلعی ) ترسیم کرد.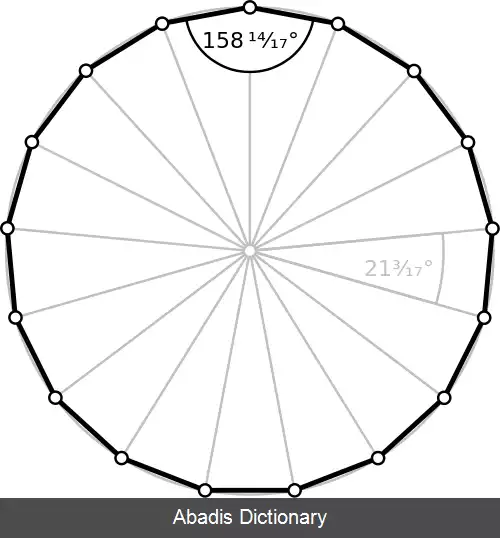
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک هفده ضلعی منتظم دارای ضلع ها و زاویه های داخلی برابر است. اندازهٔ زاویه های داخلی هر رأس آن، حدود ۱۵۸٫۸ درجه بوده و مساحت آن با استفاده از رابطهٔ زیر محاسبه می شود:
یک هفده ضلعی منتظم با استفاده از خط کش غیرمدرج و پرگار قابل ترسیم است. این موضوع در سال ۱۷۹۶ توسط کارل فریدریش گاوس ۱۹ ساله اثبات شد. [ ۲] این اثبات، نخستین پیشرفت در ترسیم چندضلعی های منتظم پس از بیش از ۲۰۰۰ سال بود. [ ۲]
اثبات گاوس، بر اساس این حقیقت بود که اولاً قابل ترسیم بودن، معادل است با قابل بیان بودن تابع های مثلثاتی زاویهٔ مشترک بر اساس عمل گرهای حسابی و ریشه دوم، و دوم اینکه این کار قابل انجام است اگر توان های اول فرد n اعداد اول فرمای متفاوتی ( به فرم F n = 2 2 n + 1 ) باشند.
بنابراین، ترسیم یک هفده ضلعی منتظم، شامل یافتن کسینوس 2 π / 17 بر حسب ریشه دوم است. گاوس در کتاب بررسی های حسابی ( Disquisitiones Arithmeticae ) خود، این رابطه را به این صورت استخراج کرده است:
ترسیم چندضلعی های منتظم با 2h ضلع، توسط اقلیدس شناخته شده بود، ولی ترسیم بر اساس اعداد فرما ( به جز ۳ و ۵ ) در ریاضیات باستان ناشناخته بود.
نخستین ترسیم صریح از هفده ضلعی در سال ۱۸۲۵ توسط یوهان ارشینگر انجام گرفت. یک روش دیگر بر اساس استفاده از دایره های کارلایل به صورت زیر است. بر اساس ترسیم یک هفده ضلعی منتظم، می توان به راحتی n - ضلعی هایی با n به صورت حاصل ضرب ۱۷ در ۳ یا ۵ ( و یا هر دو ) و هر توان ۲ ( مثلاً ۵۱ - ضلعی، ۸۵ - ضلعی، یا ۲۵۵ - ضلعی ) ترسیم کرد.


wiki: هفده ضلعی
