نیروی مرکزی
فرهنگستان زبان و ادب
دانشنامه عمومی
نیروی که در نمایش دستگاه مختصات کروی دارای فرم روبرو باشد را نیروی مرکزی ( به انگلیسی: Central force ) می نامیم: F → = f ( r ) r ^
نیروی گرانش و قانون کولن دو نمونه از نیروی مرکزی هستند. از آنجایی که تاو نیروهای مرکزی صفر است ( ▽ × F → = 0 ) ، تمام نیروهای مرکزی نیروی پایستار هستند. بنابراین می توانیم تابع انرژی پتانسیل را تعریف کنیم: V ( r ) = − ∫ r r e f r F → . d r → = − ∫ r r e f r f ( r ) d r
و r r e f ( حد پائین ) مقدار مرجع r است که به ازای آن، انرژی پتانسیل بنابر تعریف صفر می شود؛ در مورد نیروهایی از نوع توان معکوس، غالباً r r e f بی نهایت انتخاب می شود. از معادله فوق با معلوم بودن تابع نیرو، میتوان تابع انرژی پتانسیل را محاسبه کرد و همچنین برعکس، اگر تابع انرژی پتانسیل معلوم باشد می توانیم تابع نیرو را برای میدان مرکزی محاسبه کنیم: f ( r ) = − d V ( r ) d r
از مهمترین ویژگی های نیروهای مرکزی، ثابت بودن تکانه زاویه ای ذرات متحرک در میدان های مرکزی است[ ۱] : بردار ثابت L → = ، L = | m r 2 θ ˙ | = c o n s t
تمام نیروهای مرکزی امکان تشکیل مدارهای دایره ای پایدار را نمی دهند. تنها میدان های مرکزی ای اجازه تشکیل مدار دایره ای پایدار را می دهند که در نامساوی روبرو ( شرط پایداری ) صدق کنند: f ( a ) + a 3 f ′ ( a ) < 0
به عنوان مثال اگر تابع نیروی مرکزی به صورت توانی باشد ( f ( r ) = − c r n ) شرط پایداری نتیجه می دهد: − c a n − a 3 c a n − 1 < 0 ⟹ n > − 3
بنابراین نیروی عکس مجذوری ( همانند گرانش: n = − 2 ) اجازه ی ایجاد مدار دایره ای پایدار را می دهد، اما در نیرویی همانند عکس توان چهار ( n = − 4 ) مدارهای دایره ای ناپایدار هستند[ ۱] .
↑ ۱٫۰ ۱٫۱ فاؤلز، گرنت. ر ( ۱۳۸۷ ) . مکانیک تحلیلی. تهران: مرکز نشر دانشگاهی. صص. ۱۹۶و۱۹۷. شابک ۹۷۸ - ۹۶۴ - ۰۱ - ۰۶۵۹ - ۴.
• مقاله های بدون منبع از آوریل ۲۰۱۹
• مکانیک کلاسیک
• نیرو
• همه مقاله های بدون منبع
• مقاله های دارای واژگان به زبان انگلیسی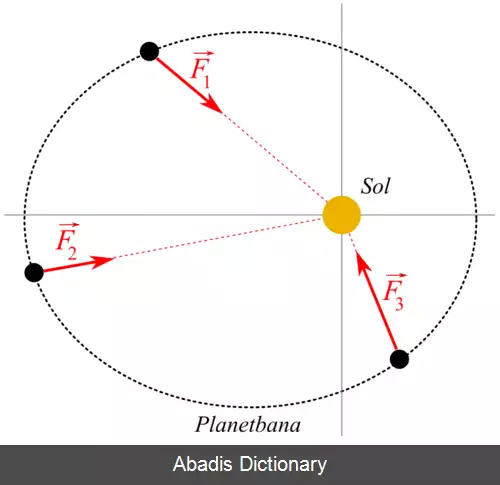
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنیروی گرانش و قانون کولن دو نمونه از نیروی مرکزی هستند. از آنجایی که تاو نیروهای مرکزی صفر است ( ▽ × F → = 0 ) ، تمام نیروهای مرکزی نیروی پایستار هستند. بنابراین می توانیم تابع انرژی پتانسیل را تعریف کنیم: V ( r ) = − ∫ r r e f r F → . d r → = − ∫ r r e f r f ( r ) d r
و r r e f ( حد پائین ) مقدار مرجع r است که به ازای آن، انرژی پتانسیل بنابر تعریف صفر می شود؛ در مورد نیروهایی از نوع توان معکوس، غالباً r r e f بی نهایت انتخاب می شود. از معادله فوق با معلوم بودن تابع نیرو، میتوان تابع انرژی پتانسیل را محاسبه کرد و همچنین برعکس، اگر تابع انرژی پتانسیل معلوم باشد می توانیم تابع نیرو را برای میدان مرکزی محاسبه کنیم: f ( r ) = − d V ( r ) d r
از مهمترین ویژگی های نیروهای مرکزی، ثابت بودن تکانه زاویه ای ذرات متحرک در میدان های مرکزی است[ ۱] : بردار ثابت L → = ، L = | m r 2 θ ˙ | = c o n s t
تمام نیروهای مرکزی امکان تشکیل مدارهای دایره ای پایدار را نمی دهند. تنها میدان های مرکزی ای اجازه تشکیل مدار دایره ای پایدار را می دهند که در نامساوی روبرو ( شرط پایداری ) صدق کنند: f ( a ) + a 3 f ′ ( a ) < 0
به عنوان مثال اگر تابع نیروی مرکزی به صورت توانی باشد ( f ( r ) = − c r n ) شرط پایداری نتیجه می دهد: − c a n − a 3 c a n − 1 < 0 ⟹ n > − 3
بنابراین نیروی عکس مجذوری ( همانند گرانش: n = − 2 ) اجازه ی ایجاد مدار دایره ای پایدار را می دهد، اما در نیرویی همانند عکس توان چهار ( n = − 4 ) مدارهای دایره ای ناپایدار هستند[ ۱] .
↑ ۱٫۰ ۱٫۱ فاؤلز، گرنت. ر ( ۱۳۸۷ ) . مکانیک تحلیلی. تهران: مرکز نشر دانشگاهی. صص. ۱۹۶و۱۹۷. شابک ۹۷۸ - ۹۶۴ - ۰۱ - ۰۶۵۹ - ۴.
• مقاله های بدون منبع از آوریل ۲۰۱۹
• مکانیک کلاسیک
• نیرو
• همه مقاله های بدون منبع
• مقاله های دارای واژگان به زبان انگلیسی

wiki: نیروی مرکزی
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
