در دینامیک، نوسان ساز وَن دِر پُل یک نوسان ساز نا - پایستار غیرخطی با میرایی است. بر طبق معادله دیفرانسیل مرتبه - دوم در زمان، تکامل می یابد:
که در آن x مختصات موقعیت است - که تابعی از زمان t است، و μ یک پارامتر اسکالر است که غیرخطی بودن و سختی میرایی را نشان می دهد.
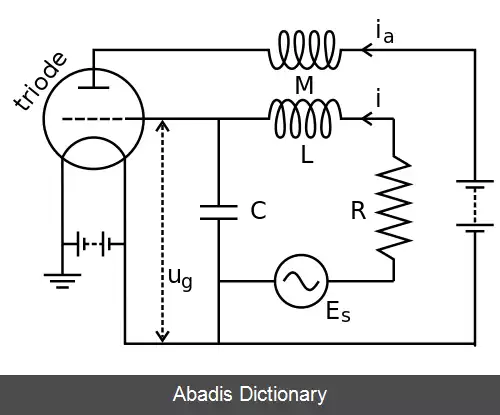
نوسان ساز ون در پل در ابتدا توسط مهندس برق و فیزیکدان هلندی بالتازار ون در پل پیشنهاد شد در حالی که وی در فیلیپس کار می کرد. [ ۱] ون در پل نوسانات پایداری پیدا کرد، [ ۲] که بعداً آنها را نوسانات آرامشی[ ۳] نامید و اکنون به عنوان نوعی چرخه حدی در مدارهای الکتریکی با استفاده از لامپ خلأ شناخته می شوند. هنگامی که این مدارها به نزدیک چرخه حدی رانده می شوند، آنها در آن فرور می افتد، یعنی سیگنال محرک جریان را به همراه خود می کشد. ون در پل و همکار وی، ون در مارک، در نشریه ماه سپتامبر سال ۱۹۲۷ در نیچر[ ۴] که در برخی از فرکانس های راه اندازی یک نویز نامنظمی شنیده می شود که بعداً مشخص شد نتیجه آشوب تعینی است. [ ۵]
معادله ون در پل از سابقه طولانی استفاده در علوم فیزیکی و زیست شناسی برخوردار است. به عنوان مثال، در زیست شناسی، فیتزهیو[ ۶] و ناگومو[ ۷] معادله را در یک میدان مسطح به عنوان مدلی برای پتانسیل های کار نورون ها گسترش دادند. معادله نیز در زلزله شناسی برای مدل دو صفحه در یک گسل زمین شناسی، [ ۸] و در مطالعات آواسازی برای مدل چپ و راست پرده صوتی نوسان گرها استفاده شده است. [ ۹]
از قضیه لینارد می توان برای اثبات وجود چرخه حدی سیستم استفاده کرد. اعمال تبدیل لینارد y = x − x 3 / 3 − x ˙ / μ ، که در اینجا این نقطه مشتق زمان را نشان می دهد، نوسان ساز ون در پل را می توان به شکل دو بعدی آن نوشت:[ ۱۰]
شکل دیگری که معمولاً بر اساس تبدیل y = x ˙ استفاده می شود منجر به:
دو رژیم جالب برای مشخصه های نوسان ساز غیرتحریک شده عبارتند از:[ ۱۱]
• وقتی μ = ۰، یعنی هیچ تابع میرایی وجود ندارد، این معادله تبدیل می شود:
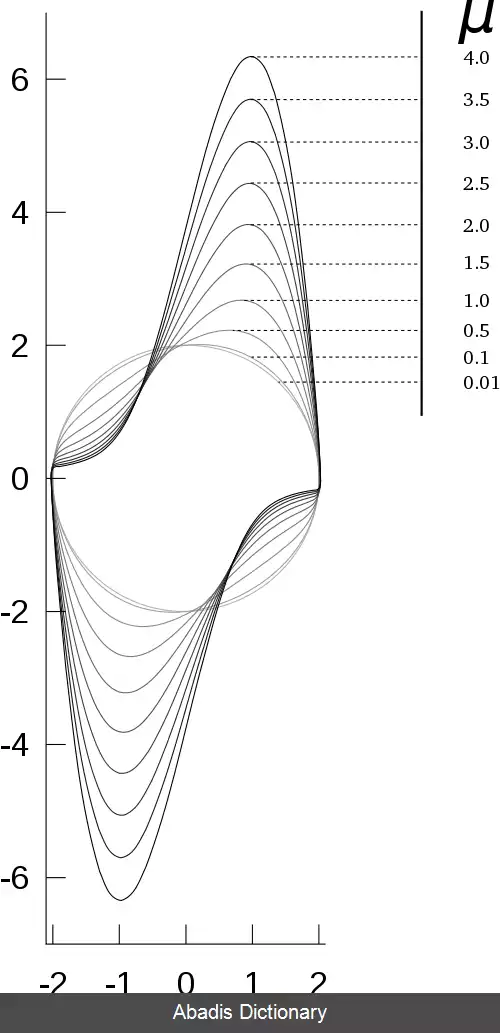
• وقتی μ > ۰ باشد، سیستم وارد یک چرخه حدی خواهد شد. نزدیک x = dx/dt = ۰، سیستم ناپایدار است و دور از مبدأ، سیستم میرایی دارد.
• نوسان ساز ون در پل یک جواب دقیق و تحلیلی ندارد. [ ۱۲] اگر f ( x ) در معادله لینارد یک تابع ثابت قطعه ای باشد، چنین جوابی برای چرخه حدی وجود دارد.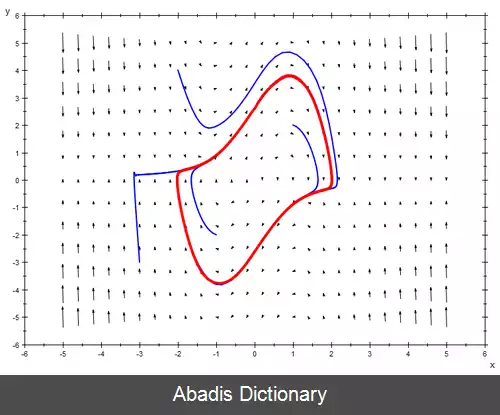
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه در آن x مختصات موقعیت است - که تابعی از زمان t است، و μ یک پارامتر اسکالر است که غیرخطی بودن و سختی میرایی را نشان می دهد.
نوسان ساز ون در پل در ابتدا توسط مهندس برق و فیزیکدان هلندی بالتازار ون در پل پیشنهاد شد در حالی که وی در فیلیپس کار می کرد. [ ۱] ون در پل نوسانات پایداری پیدا کرد، [ ۲] که بعداً آنها را نوسانات آرامشی[ ۳] نامید و اکنون به عنوان نوعی چرخه حدی در مدارهای الکتریکی با استفاده از لامپ خلأ شناخته می شوند. هنگامی که این مدارها به نزدیک چرخه حدی رانده می شوند، آنها در آن فرور می افتد، یعنی سیگنال محرک جریان را به همراه خود می کشد. ون در پل و همکار وی، ون در مارک، در نشریه ماه سپتامبر سال ۱۹۲۷ در نیچر[ ۴] که در برخی از فرکانس های راه اندازی یک نویز نامنظمی شنیده می شود که بعداً مشخص شد نتیجه آشوب تعینی است. [ ۵]
معادله ون در پل از سابقه طولانی استفاده در علوم فیزیکی و زیست شناسی برخوردار است. به عنوان مثال، در زیست شناسی، فیتزهیو[ ۶] و ناگومو[ ۷] معادله را در یک میدان مسطح به عنوان مدلی برای پتانسیل های کار نورون ها گسترش دادند. معادله نیز در زلزله شناسی برای مدل دو صفحه در یک گسل زمین شناسی، [ ۸] و در مطالعات آواسازی برای مدل چپ و راست پرده صوتی نوسان گرها استفاده شده است. [ ۹]
از قضیه لینارد می توان برای اثبات وجود چرخه حدی سیستم استفاده کرد. اعمال تبدیل لینارد y = x − x 3 / 3 − x ˙ / μ ، که در اینجا این نقطه مشتق زمان را نشان می دهد، نوسان ساز ون در پل را می توان به شکل دو بعدی آن نوشت:[ ۱۰]
شکل دیگری که معمولاً بر اساس تبدیل y = x ˙ استفاده می شود منجر به:
دو رژیم جالب برای مشخصه های نوسان ساز غیرتحریک شده عبارتند از:[ ۱۱]
• وقتی μ = ۰، یعنی هیچ تابع میرایی وجود ندارد، این معادله تبدیل می شود:
• وقتی μ > ۰ باشد، سیستم وارد یک چرخه حدی خواهد شد. نزدیک x = dx/dt = ۰، سیستم ناپایدار است و دور از مبدأ، سیستم میرایی دارد.
• نوسان ساز ون در پل یک جواب دقیق و تحلیلی ندارد. [ ۱۲] اگر f ( x ) در معادله لینارد یک تابع ثابت قطعه ای باشد، چنین جوابی برای چرخه حدی وجود دارد.





wiki: نوسان ساز ون در پل
