نمودار هَسه ( به انگلیسی: Hasse diagram ) یک نمودار ریاضی برای نمایش یک مجموعه جزئاً مرتب متناهی است. برای یک مجموعه با ترتیب جزئی ( ≥، P ) هر عضو مجموعه P با یک رأس در گراف نشان داده می شود و برای نشان دادن رابطه بین اعضای مجموعه تنها به رابطه های پادمتقارن بسنده می شود.
از آن جایی که در گرافِ رابطه پادمتقارن، هیچ یالی نمی تواند دوطرفه باشد، نمودار هسه طوری رسم می گردد که جهت هر یال رو به بالا فرض شود.
این نکته قابل ذکر است که نمودار هسه دارای دور جهت دار نیست.
اگرچه نمودار های هسه برای برخورد با مجموعه مرتب جزئی ساده اند، اما کشیدن یک نمودار هسه ی خوب دشوار است زیرا روش های زیادی برای کشیدن نمودار هسه با توجه به مجموعه ی مرتب جزئی وجود دارد ( نمودار هسه برای یک مجموعه ی مرتب جزئی یکتا نیست ) .
یک روش ساده برای رسم نمودار هسه این است که رسم را با یک عضو مینیمال شروع کنیم و سپس با رسم عضوهای بزرگ تر نمودار مورد نظر را رسم کنیم که معمولاً شامل نتایج منفی زیر می باشد:
1. تقارن در آن وجود ندارد.
2. ساختار نظم داخلی به راحتی در آن از بین می رود.
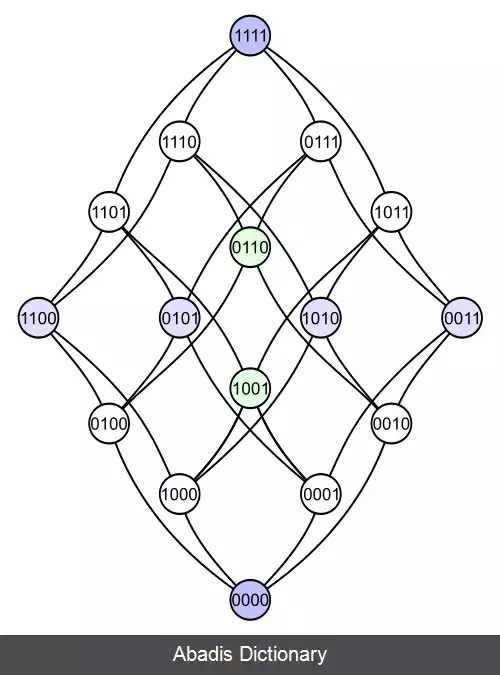
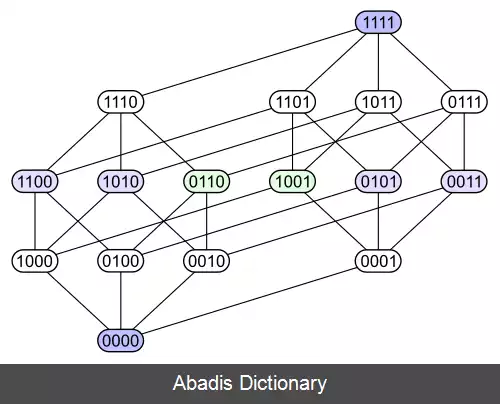
مثال های زیر نشان دهنده ی این موضوع است. که یک مجموعه ی توانی همراه چهار عضو توسط رابطه زیر مجموعه بودن تنظیم شده اند. هر عضو از زیر مجموعه توانی به صورت باینری نشانه گذاری شده اند و نشان دهنده این است که یک عضو خاص در زیرمجموعه، یک است یا صفر.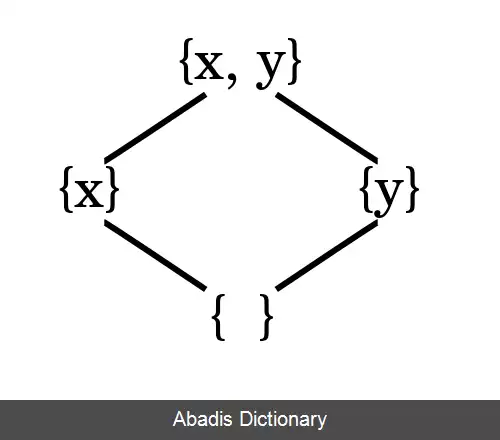
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز آن جایی که در گرافِ رابطه پادمتقارن، هیچ یالی نمی تواند دوطرفه باشد، نمودار هسه طوری رسم می گردد که جهت هر یال رو به بالا فرض شود.
این نکته قابل ذکر است که نمودار هسه دارای دور جهت دار نیست.
اگرچه نمودار های هسه برای برخورد با مجموعه مرتب جزئی ساده اند، اما کشیدن یک نمودار هسه ی خوب دشوار است زیرا روش های زیادی برای کشیدن نمودار هسه با توجه به مجموعه ی مرتب جزئی وجود دارد ( نمودار هسه برای یک مجموعه ی مرتب جزئی یکتا نیست ) .
یک روش ساده برای رسم نمودار هسه این است که رسم را با یک عضو مینیمال شروع کنیم و سپس با رسم عضوهای بزرگ تر نمودار مورد نظر را رسم کنیم که معمولاً شامل نتایج منفی زیر می باشد:
1. تقارن در آن وجود ندارد.
2. ساختار نظم داخلی به راحتی در آن از بین می رود.
مثال های زیر نشان دهنده ی این موضوع است. که یک مجموعه ی توانی همراه چهار عضو توسط رابطه زیر مجموعه بودن تنظیم شده اند. هر عضو از زیر مجموعه توانی به صورت باینری نشانه گذاری شده اند و نشان دهنده این است که یک عضو خاص در زیرمجموعه، یک است یا صفر.



wiki: نمودار هسه
