در ریاضیات، نظریه گالوا ارتباطی بین نظریه میدان ها و نظریه گروه ها ایجاد می کند. با استفاده از نظریۀ گالوا، برخی از مسائل نظریۀ میدان ها را می توان به مسائل نظریۀ گروه ها تقلیل داد، که از جنبه هایی ساده تر بوده و بهتر فهمیده می شود. همچنین با استفاده از آن برخی مسائل کلاسیک باستانی لاینحل، حل شدند؛ مثل مسئلۀ تضعیف مکعب، تثلیث زاویه ( مسئله سوم باستانی، یعنی تربیع دایره هم حل ناپذیر است، اما حل ناپذیری اش توسط روش های دیگری نشان داده شده ) ، نشان دادن این که هیچ فرمولی برای ریشه های چند جمله ای های درجۀ پنج وجود ندارد و نشان دادن این که کدام چندضلعی ها ساختنی هستند.
این موضوع ریاضیاتی به افتخار اواریست گالوا که ریشه ها را برای مطالعۀ چندجمله ای ها معرفی کرد نامگذاری شد. او چندجمله ای هایی که حل پذیر با رادیکال ها هستند را براساس خواص گروه جایگشت های ریشه هایشان مشخصه سازی کرد، یک چند جمله ای توسط رادیکال ها حلپذیر است اگر ریشه هایش را بتوان توسط فرمول هایی شامل اعداد صحیح، ریشه های nام و چهار عمل پایه ای حساب بیان کرد.
این نظریه توسط ریچارد ددکیند، لئوپولد کرونکر، امیل آرتین و دیگرانی که به طور خاص گروه جایگشت ریشه ها را به صورت گروه خودریختی های یک توسیع میدانی توصیف کردند، در میان ریاضیدانان معروف شده و توسعه پیدا کرد.
نظریه گالوا به اتصالات گالوایی و نظریۀ گالوای گروتندیک تعمیم یافته است.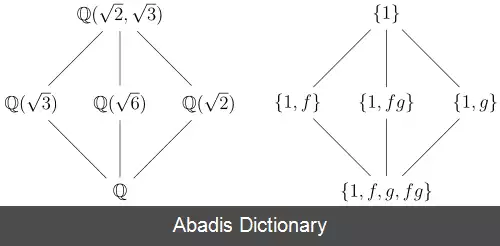
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین موضوع ریاضیاتی به افتخار اواریست گالوا که ریشه ها را برای مطالعۀ چندجمله ای ها معرفی کرد نامگذاری شد. او چندجمله ای هایی که حل پذیر با رادیکال ها هستند را براساس خواص گروه جایگشت های ریشه هایشان مشخصه سازی کرد، یک چند جمله ای توسط رادیکال ها حلپذیر است اگر ریشه هایش را بتوان توسط فرمول هایی شامل اعداد صحیح، ریشه های nام و چهار عمل پایه ای حساب بیان کرد.
این نظریه توسط ریچارد ددکیند، لئوپولد کرونکر، امیل آرتین و دیگرانی که به طور خاص گروه جایگشت ریشه ها را به صورت گروه خودریختی های یک توسیع میدانی توصیف کردند، در میان ریاضیدانان معروف شده و توسعه پیدا کرد.
نظریه گالوا به اتصالات گالوایی و نظریۀ گالوای گروتندیک تعمیم یافته است.

wiki: نظریه گالوا
