نظریه توالی یابی دی ان ای به تلاش هایی جهت طرح کردن مبانی تحلیلی توالی یابی دی ان ای می گویند. توالی یابی دی ان ای فرایندی است که در طی آن ترتیب نوکلئوتیدهای درون مولکول DNA مشخص می شود. نتایج ریاضی محض بدست آمده نظریه توالی یابی دی ان ای در عمل عوامل مهمی در توالی یابی نیستند. در نتیجه توسعه نظریه توالی یابی در حوزه ریاضیات کاربردی ادامه پیدا کرد. [ ۱]
همه ی روش های اصلی توالی یابی دی ان ای، بر پایه ی خواندن تکه های دی ان ای و بازسازی دی ان ای از روی این تکه ها، یا به وسیله بازسازی توالی و یا هم ترازسازی توالی است. مساله پوشش، یک مساله انتزاعی برای هردوی آن هاست.
بیش از یک قرن، ریاضیدانان ویژگی های انتزاعی پوشش را مطالعه قرار دادند. با این حال، کاربردهای مستقیم نتایج آن ها به طور کلی امکان پذیر نبوده. به این معنا که الگوریتم های بدست آمده از آن ها زمان زیادی برای اجرا نیاز دارند. یکی از مثال های این الگوریتم ها، پیکربندی استیون است. [ ۲]
فرض کنید فرایند بالا را به این شکل مدل کنیم که L طول تکه رشته ها باشد و G طول دنباله هدف ( دی ان ای ) باشد. اگر L به صورت تصادفی انتخاب شده باشد احتمال این که یک نوکلئوتید در تکه L باشد برابر L G − L + 1 است و اگر فرض کنیم L ≪ G در اینصورت این احتمال برابر است با L G پس احتمال اینکه این نوکلئوتید در تکه L نباشد برابر 1 − L G حال اگر N تکه داشته باشیم این احتمال برابر N می شود. متغیرتصادفی C را به اینصورت تعریف می کنیم که اگر این نوکلئوتید توسط حداقل یک تکه پوشیده شود برابر 1 ، وگرنه 0 شود.
E = P r = 1 − N
و اگر فرض کنیم N ≫ 1 ( که در بسیاری از موارد فرض درستی است ) داریم:
N ∼ e − N L G ⟹ E = 1 − e − N L G
که R = N L G را افزونگی می گویند. [ ۳]
در سال ۱۹۸۸، اریک لندر و مایکل واترمن یک مقاله مهم در این زمینه منتشر کردند. تمرکز آن ها روی مسأله نگاشت ژن بود که در حالت انتزاعی خیلی به مسأله توالی یابی نزدیک است. مدل آن ها در پروژه ژنوم انسان نیز استفاده شد و همچنان نقش اساسی ای در توالی یابی دی ان ای دارد. یکی از پراستفاده ترین نتایج مدل آن ها بدست آوردن امیدریاضی تعداد وربستهاست. [ ۴]
E = N e − R
ترفند توقفگاه برای توالی یابی مانند توقف خودروها در کنار جدول خیابان هاست. هر ماشین یک تکه است و جدول کنار خیابان توالی دی ان ای خواسته شده است. در این ترفند هر تکه طوری انتخاب می شود که با تکه های قبلی اشتراک نداشته باشد. مانند خودروهای متوقف شده در کنار خیابان که با هم فاصله دارند، بین تکه ها نیز فاصله هایی وجود دارد که برای پر کردن این فاصله ها ممکن است مجبور باشیم هزینه زیادی بپردازیم. [ ۵]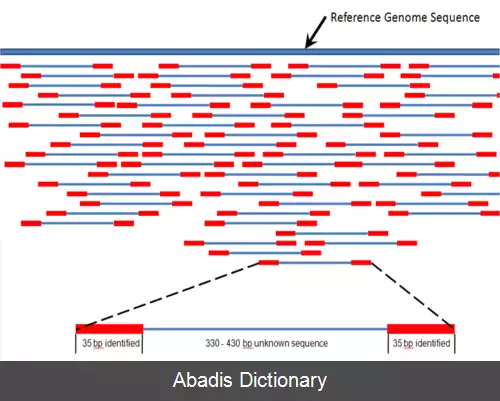
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهمه ی روش های اصلی توالی یابی دی ان ای، بر پایه ی خواندن تکه های دی ان ای و بازسازی دی ان ای از روی این تکه ها، یا به وسیله بازسازی توالی و یا هم ترازسازی توالی است. مساله پوشش، یک مساله انتزاعی برای هردوی آن هاست.
بیش از یک قرن، ریاضیدانان ویژگی های انتزاعی پوشش را مطالعه قرار دادند. با این حال، کاربردهای مستقیم نتایج آن ها به طور کلی امکان پذیر نبوده. به این معنا که الگوریتم های بدست آمده از آن ها زمان زیادی برای اجرا نیاز دارند. یکی از مثال های این الگوریتم ها، پیکربندی استیون است. [ ۲]
فرض کنید فرایند بالا را به این شکل مدل کنیم که L طول تکه رشته ها باشد و G طول دنباله هدف ( دی ان ای ) باشد. اگر L به صورت تصادفی انتخاب شده باشد احتمال این که یک نوکلئوتید در تکه L باشد برابر L G − L + 1 است و اگر فرض کنیم L ≪ G در اینصورت این احتمال برابر است با L G پس احتمال اینکه این نوکلئوتید در تکه L نباشد برابر 1 − L G حال اگر N تکه داشته باشیم این احتمال برابر N می شود. متغیرتصادفی C را به اینصورت تعریف می کنیم که اگر این نوکلئوتید توسط حداقل یک تکه پوشیده شود برابر 1 ، وگرنه 0 شود.
E = P r = 1 − N
و اگر فرض کنیم N ≫ 1 ( که در بسیاری از موارد فرض درستی است ) داریم:
N ∼ e − N L G ⟹ E = 1 − e − N L G
که R = N L G را افزونگی می گویند. [ ۳]
در سال ۱۹۸۸، اریک لندر و مایکل واترمن یک مقاله مهم در این زمینه منتشر کردند. تمرکز آن ها روی مسأله نگاشت ژن بود که در حالت انتزاعی خیلی به مسأله توالی یابی نزدیک است. مدل آن ها در پروژه ژنوم انسان نیز استفاده شد و همچنان نقش اساسی ای در توالی یابی دی ان ای دارد. یکی از پراستفاده ترین نتایج مدل آن ها بدست آوردن امیدریاضی تعداد وربستهاست. [ ۴]
E = N e − R
ترفند توقفگاه برای توالی یابی مانند توقف خودروها در کنار جدول خیابان هاست. هر ماشین یک تکه است و جدول کنار خیابان توالی دی ان ای خواسته شده است. در این ترفند هر تکه طوری انتخاب می شود که با تکه های قبلی اشتراک نداشته باشد. مانند خودروهای متوقف شده در کنار خیابان که با هم فاصله دارند، بین تکه ها نیز فاصله هایی وجود دارد که برای پر کردن این فاصله ها ممکن است مجبور باشیم هزینه زیادی بپردازیم. [ ۵]

