در ریاضیات، نظریه تراوِش به توضیح رفتار خوشه ها در گراف های تصادفی می پردازد. از کاربردهای نظریه تراوش می توان در علم مواد و دیگر حوزه هایی که در مورد نفوذ و تراوش مواد بحث می کنند استفاده کرد.
علت نامگذاری نظریه تراوش و سرآغاز آن این سؤال است، فرض کنید مایعی در بالای جسمی منفذدار ریخته شده است، آیا می تواند با گذر از منافذ این جسم خود را به سطح پایینی آن برساند؟ این سؤال که در دنیای واقعی و فیزیک مطرح می شود در ریاضیات به صورت شبکهٔ سه بعدی از n*n*n راس مدل سازی می شود، به هرکدام از این رئوس اتاقک هم گفته می شود، یال بین هر دو راس می تواند مستقل از بقیه یال ها به احتمال p باز باشد ( اجازه انتقال ماده را بدهد ) یا به احتمال 1 - p بسته باشد. در اینصورت برای هر p داده شده احتمال اینکه مسیری از یال های باز از رئوس بالایی به رئوس پایینی وجود داشته باشد چقدر است؟ هدف اولیه این سؤال بررسی رفتار گراف برای nهای بزرگ می باشد.
این مسئله که تراوش زنجیره ای نامیده می شود اولین بار در ریاضیات توسط «Broadbent» و «Hammersley» مطرح شده و تا به حال توسط تعدادی از فیزیکدانان و ریاضیدانان مشتاقانه دنبال شده است.
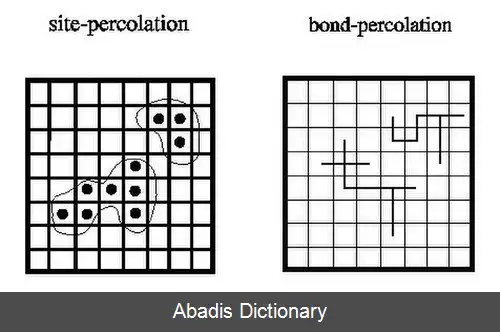
در مدل سازی دیگری با تفاوت کمی برای بدست آوردن گراف تصادفی، فرض می کنیم که هر کدام از اتاقک ها به احتمال p «پر» و با احتمال ۱ - p «خالی» هستند ( یال ها در این مدل حذف شده اند ) . در این مسئله که تراوش اتاقکی نامیده می شود سؤال مانند قبل است: برای هر p داده شده احتمال اینکه مسیری از اتاقک های پر از بالا به سطح پایینی وجود داشته باشد چقدر است؟
البته همین سؤالات را می توان برای هر ابعادی از شبکه مطرح کرد. همان طور که واضح است، بررسی یک شبکه نامحدود نسبت به یک شبکه با ابعاد بزرگ ساده تر است. در این حالت سؤال بالا به این صورت در می آید: آیا خوشهٔ بازبینهایت وجود دارد؟ یا به عبارتی آیا در میان رأس های متصل به هم مسیری به طول بینهایت در داخل شبکه وجود دارد؟ با توجه به قانون کولموگوروف، [ * ۱] برای هر p داده شده، احتمال اینکه چنین خوشه ای وجود داشته باشد یا یک است یا صفر. از آنجایی که این احتمال تابعی صعودی از p است، یک نقطهٔ بحرانی از p وجود دارد ( که با pc نشان داده می شود ) که قبل از این نقطه به احتمال ۰ و بعد از آن به احتمال ۱ چنین مسیری وجود خواهد داشت. در عمل این تغییر فاز بحرانی به راحتی قابل مشاهده است. حتی اگر n به مانند ۱۰۰ کوچک هم باشد، احتمال اینکه مسیری از بالا به سطح پایینی وجود داشته باشد در بازه ای نزدیک به pc از نزدیکی های صفر تا نزدیکی های یک به شدت افزایش می یابد.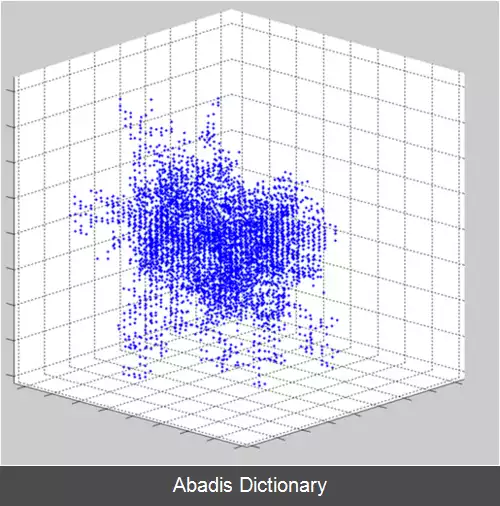

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعلت نامگذاری نظریه تراوش و سرآغاز آن این سؤال است، فرض کنید مایعی در بالای جسمی منفذدار ریخته شده است، آیا می تواند با گذر از منافذ این جسم خود را به سطح پایینی آن برساند؟ این سؤال که در دنیای واقعی و فیزیک مطرح می شود در ریاضیات به صورت شبکهٔ سه بعدی از n*n*n راس مدل سازی می شود، به هرکدام از این رئوس اتاقک هم گفته می شود، یال بین هر دو راس می تواند مستقل از بقیه یال ها به احتمال p باز باشد ( اجازه انتقال ماده را بدهد ) یا به احتمال 1 - p بسته باشد. در اینصورت برای هر p داده شده احتمال اینکه مسیری از یال های باز از رئوس بالایی به رئوس پایینی وجود داشته باشد چقدر است؟ هدف اولیه این سؤال بررسی رفتار گراف برای nهای بزرگ می باشد.
این مسئله که تراوش زنجیره ای نامیده می شود اولین بار در ریاضیات توسط «Broadbent» و «Hammersley» مطرح شده و تا به حال توسط تعدادی از فیزیکدانان و ریاضیدانان مشتاقانه دنبال شده است.
در مدل سازی دیگری با تفاوت کمی برای بدست آوردن گراف تصادفی، فرض می کنیم که هر کدام از اتاقک ها به احتمال p «پر» و با احتمال ۱ - p «خالی» هستند ( یال ها در این مدل حذف شده اند ) . در این مسئله که تراوش اتاقکی نامیده می شود سؤال مانند قبل است: برای هر p داده شده احتمال اینکه مسیری از اتاقک های پر از بالا به سطح پایینی وجود داشته باشد چقدر است؟
البته همین سؤالات را می توان برای هر ابعادی از شبکه مطرح کرد. همان طور که واضح است، بررسی یک شبکه نامحدود نسبت به یک شبکه با ابعاد بزرگ ساده تر است. در این حالت سؤال بالا به این صورت در می آید: آیا خوشهٔ بازبینهایت وجود دارد؟ یا به عبارتی آیا در میان رأس های متصل به هم مسیری به طول بینهایت در داخل شبکه وجود دارد؟ با توجه به قانون کولموگوروف، [ * ۱] برای هر p داده شده، احتمال اینکه چنین خوشه ای وجود داشته باشد یا یک است یا صفر. از آنجایی که این احتمال تابعی صعودی از p است، یک نقطهٔ بحرانی از p وجود دارد ( که با pc نشان داده می شود ) که قبل از این نقطه به احتمال ۰ و بعد از آن به احتمال ۱ چنین مسیری وجود خواهد داشت. در عمل این تغییر فاز بحرانی به راحتی قابل مشاهده است. حتی اگر n به مانند ۱۰۰ کوچک هم باشد، احتمال اینکه مسیری از بالا به سطح پایینی وجود داشته باشد در بازه ای نزدیک به pc از نزدیکی های صفر تا نزدیکی های یک به شدت افزایش می یابد.



wiki: نظریه تراوش
