نظریه تجدید، شاخه ای از نظریه احتمال است که فرایندهای پواسون را به زمان های نگهداری اختیاری عمومیت می دهد. کاربردهایی شامل محاسبه زمان انتظار برای میمونی که به صورت تصادفی به صفحه کلید ضربه می زند تا کلمه مک بت را تایپ کند و به محاسبه مزایای دراز مدت از سیاست های تضمینی مختلف بپردازد.
فرایند تجدید، تعمیم یافتهٔ فرایند پواسون است. فرایند پواسون ذاتاً یک فرایند پیوسته مارکوف می باشد که توزیع مستقل یکسان از زمان های نگهداری شده از هر عدد صحیح i با توزیع نمایی قبل از رسیدن به عدد صحیح بعدی i + 1 با احتمال یک است. در رویه غیررسمی ممکن است نظریه تجدید را به همین صورت تعریف کنیم به جز اینکه زمان های نگهداری شده از توزیع عمومی تری گرفته شده اند. ( توجه داشته باشید که مشخصات توزیع های مستقل ویکسان ( متغیرهای تصادفی مستقل با توزیع یکسان ) از زمان های نگهداری شده حفظ می شوند. )
فرض کنید S 1 , S 2 , S 3 , S 4 , S 5 , … دنباله ای از متغیرهای تصادفی مستقل وتوزیع شده یکسان باشد مثل: 0 < E < ∞ . فرض می کنیم متغیر تصادفی S i به عنوان i امین زمان ثبت شده باشد که برای هر ۰< "n" به صورت زیر تعریف می کنیم؛
هر J n مربوط به n امین پرش زمانی است وبازه به عنوان بازهٔ تجدید شناخته می شود پس متغیر تصادفی ( X t ) t ≥ 0 به صورت زیر داده می شود. X t = ∑ n = 1 ∞ I { J n ≤ t } = sup { n : J n ≤ t } به طوری که I تابع شاخص مطرح است بیان کننده تعداد پرش است که در زمان t رخ داده است و به عنوان فرایند تجدید خوانده می شود.
ممکن است شخصی فکر کند زمان های نگهداری شده { S i : i ≥ 1 } به عنوان زمان طی شده قبل از یک خرابی ماشین را در i مین بار، در زمان آخرین خرابی باشد. به این فرض توجه کنید که ممکن است ماشین فوراً درست شده باشدوما کلاک را فوراً ریست می کنیم ) . در این تفسیر زمان های پرش { J n : n ≥ 1 } ، زمان های موفقیت را ثبت می کنند که در کد یک از آن ها ماشین خراب شده و فرایند تجدید X t ، تعداد زمانهایی که تا این جا در زمان داده شده t باید تعمیر شده باشد را ثبت می کند. اگر چه این مطلب برای فهم فرایند تجدید با وجود شکل مختصر خود، مؤثر است چون ممکن است برای مدل کردن تعداد زیادی از موقعیت های عملی وابسته استفاده شود ارتباط خیلی نزدیکی با عملکرد ماشین نداشته باشد.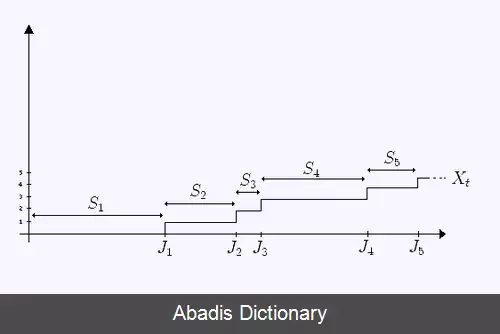
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرایند تجدید، تعمیم یافتهٔ فرایند پواسون است. فرایند پواسون ذاتاً یک فرایند پیوسته مارکوف می باشد که توزیع مستقل یکسان از زمان های نگهداری شده از هر عدد صحیح i با توزیع نمایی قبل از رسیدن به عدد صحیح بعدی i + 1 با احتمال یک است. در رویه غیررسمی ممکن است نظریه تجدید را به همین صورت تعریف کنیم به جز اینکه زمان های نگهداری شده از توزیع عمومی تری گرفته شده اند. ( توجه داشته باشید که مشخصات توزیع های مستقل ویکسان ( متغیرهای تصادفی مستقل با توزیع یکسان ) از زمان های نگهداری شده حفظ می شوند. )
فرض کنید S 1 , S 2 , S 3 , S 4 , S 5 , … دنباله ای از متغیرهای تصادفی مستقل وتوزیع شده یکسان باشد مثل: 0 < E < ∞ . فرض می کنیم متغیر تصادفی S i به عنوان i امین زمان ثبت شده باشد که برای هر ۰< "n" به صورت زیر تعریف می کنیم؛
هر J n مربوط به n امین پرش زمانی است وبازه به عنوان بازهٔ تجدید شناخته می شود پس متغیر تصادفی ( X t ) t ≥ 0 به صورت زیر داده می شود. X t = ∑ n = 1 ∞ I { J n ≤ t } = sup { n : J n ≤ t } به طوری که I تابع شاخص مطرح است بیان کننده تعداد پرش است که در زمان t رخ داده است و به عنوان فرایند تجدید خوانده می شود.
ممکن است شخصی فکر کند زمان های نگهداری شده { S i : i ≥ 1 } به عنوان زمان طی شده قبل از یک خرابی ماشین را در i مین بار، در زمان آخرین خرابی باشد. به این فرض توجه کنید که ممکن است ماشین فوراً درست شده باشدوما کلاک را فوراً ریست می کنیم ) . در این تفسیر زمان های پرش { J n : n ≥ 1 } ، زمان های موفقیت را ثبت می کنند که در کد یک از آن ها ماشین خراب شده و فرایند تجدید X t ، تعداد زمانهایی که تا این جا در زمان داده شده t باید تعمیر شده باشد را ثبت می کند. اگر چه این مطلب برای فهم فرایند تجدید با وجود شکل مختصر خود، مؤثر است چون ممکن است برای مدل کردن تعداد زیادی از موقعیت های عملی وابسته استفاده شود ارتباط خیلی نزدیکی با عملکرد ماشین نداشته باشد.


wiki: نظریه تجدید
