نرم کننده هسته یا هموارساز هسته ( به انگلیسی: Kernel smoother ) ، یک تکنیک آماری برای برآورد ارزش واقعی تابع f : R p → R با استفاده از میانگین وزنی همسایه های آن است. در اینجا وزن ها به وسیلهٔ هسته مشخص می شوند. این وزن ها به صورتی است که همسایه های نزدیک تر وزن بیشتری می گیرند. تابع به دست آمده به وسیلهٔ این روش هموار بوده و درجهٔ همواری آن با استفاده از یک پارامتر کنترل می شود. هموارسازی به کمک هسته، نوعی میانگین گیری متحرک می باشد. نرم کننده هسته می تواند توابع صاف تر و نرم تری از یک متغیر تصادفی را پدیدآورد.
K h λ ( X 0 , X ) یک هسته به صورت زیر می باشد:
K h λ ( X 0 , X ) = D ( ‖ X − X 0 ‖ h λ ( X 0 ) )
که در آن
• X , X 0 ∈ R p {\displaystyle X, X_{0}\in \mathbb {R} ^{p}}
• ‖ ⋅ ‖ {\displaystyle \left\|\cdot \right\|} فاصله اقلیدسی
• h λ ( X 0 ) {\displaystyle h_{\lambda } ( X_{0} ) } یک پارامتر مثبت ( شعاع هسته )
• D ( t ) یک تابع با با مقادیر مثبت بوده که مقادیر آن با بیشتر شدن فاصلهٔ X 0 {\displaystyle X_{0}} و X {\displaystyle X} کاهش می یابد ( یا حداقل افزایش نمی یابد ) .
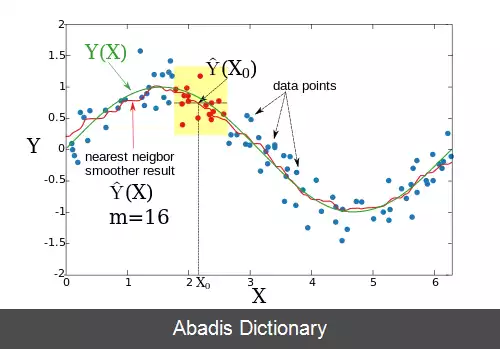
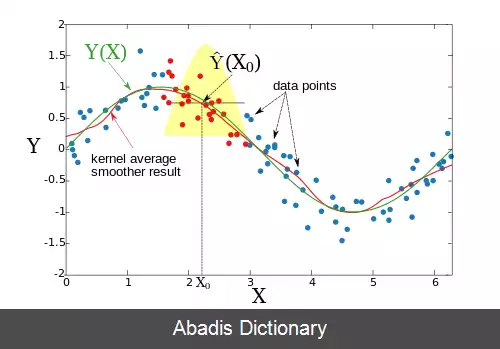
به عنوان مثال فرض کنید که Y ( X ) : R p → R یک تابع پیوسته می باشد روی X می باشد. با استفاده از هستهٔ نادارایا - واتسون[ ۱] که یک هستهٔ میانگین وزنی است، می توان تابع توزیع را به صورت زیر برآورد کرد.
Y ^ ( X 0 ) = ∑ i = 1 N K h λ ( X 0 , X i ) Y ( X i ) ∑ i = 1 N K h λ ( X 0 , X i )
• N تعداد نمونه های مشاهده شده است.
• Y ( X i ) {\displaystyle Y ( X{i} ) } مشاهدهٔ دیده شده در نقطهٔ X i {\displaystyle X{i}} است.
در ادامه به بررسی چند مورد خاص از نرم کننده های هسته می پردازیم.
هسته گاوسی یکی از پرکاربردترین هسته ها است و با معادله زیر بیان می شود.
K ( X 0 , X i ) = exp ( − ( X 0 − X i ) 2 2 b 2 )
که در اینجا b عددی است که با استفاده از آن می توان میزان نرمی نمودار را کنترل کرد و یک اسکالر می باشد.
با افزایش مقدار b شعاع هسته بزرگ تر شده و در نتیجه نقاط دورتر نیز سهم بیشتری در میانگین گیری به دست می آورند؛ بنابراین نتیجه هموارتر خواهد بود. هرچه b به صفر نزدیک تر باشد، برآوردگر نوسان بیشتری خواهد داشت.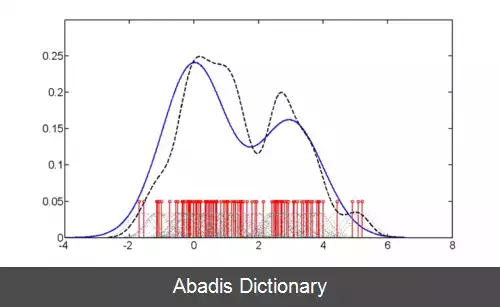
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفK h λ ( X 0 , X ) یک هسته به صورت زیر می باشد:
K h λ ( X 0 , X ) = D ( ‖ X − X 0 ‖ h λ ( X 0 ) )
که در آن
• X , X 0 ∈ R p {\displaystyle X, X_{0}\in \mathbb {R} ^{p}}
• ‖ ⋅ ‖ {\displaystyle \left\|\cdot \right\|} فاصله اقلیدسی
• h λ ( X 0 ) {\displaystyle h_{\lambda } ( X_{0} ) } یک پارامتر مثبت ( شعاع هسته )
• D ( t ) یک تابع با با مقادیر مثبت بوده که مقادیر آن با بیشتر شدن فاصلهٔ X 0 {\displaystyle X_{0}} و X {\displaystyle X} کاهش می یابد ( یا حداقل افزایش نمی یابد ) .
به عنوان مثال فرض کنید که Y ( X ) : R p → R یک تابع پیوسته می باشد روی X می باشد. با استفاده از هستهٔ نادارایا - واتسون[ ۱] که یک هستهٔ میانگین وزنی است، می توان تابع توزیع را به صورت زیر برآورد کرد.
Y ^ ( X 0 ) = ∑ i = 1 N K h λ ( X 0 , X i ) Y ( X i ) ∑ i = 1 N K h λ ( X 0 , X i )
• N تعداد نمونه های مشاهده شده است.
• Y ( X i ) {\displaystyle Y ( X{i} ) } مشاهدهٔ دیده شده در نقطهٔ X i {\displaystyle X{i}} است.
در ادامه به بررسی چند مورد خاص از نرم کننده های هسته می پردازیم.
هسته گاوسی یکی از پرکاربردترین هسته ها است و با معادله زیر بیان می شود.
K ( X 0 , X i ) = exp ( − ( X 0 − X i ) 2 2 b 2 )
که در اینجا b عددی است که با استفاده از آن می توان میزان نرمی نمودار را کنترل کرد و یک اسکالر می باشد.
با افزایش مقدار b شعاع هسته بزرگ تر شده و در نتیجه نقاط دورتر نیز سهم بیشتری در میانگین گیری به دست می آورند؛ بنابراین نتیجه هموارتر خواهد بود. هرچه b به صفر نزدیک تر باشد، برآوردگر نوسان بیشتری خواهد داشت.




wiki: نرم کننده هسته
