در آنالیز حقیقی، نابرابری برنولی ( نام گذاری شده به نام ژاکوب برنولی ) نابرابری ای است که کران پایین را برای توان های ( 1 + x ) مشخص می کند.
این نابرابری بیان می کند که برای هر عدد صحیح مانند r که r ≥ 0 و هر عدد حقیقی مانند x که x ≥ −1 داریم:
اگر r زوج باشد آنگاه نابرابری برای تمام اعداد حقیقی x برقرار است.
از نابرابری برنولی معمولاً به عنوان یک پله مهم در اثبات دیگر نابرابری ها در ریاضیات استفاده می شود. خود این نابرابری نیز را می توان به کمک استقرای ریاضی اثبات کرد.
برای r = 0، ( 1 + x ) 0 ≥ 1 + 0 x هم ارز با 1 ≤ 1 می باشد که صحیح است.
حال فرض کنید حکم برای r = k ( k عددی مثبت ) برقرار است. داریم:
و از آنجا:
اما از آنجایی که kx2 ≥ 0 داریم:
در نتیجه:
یعنی حکم برای r = k + 1 برقرار است.
بنابراین با اسقراء نتیجه می گیریم که حکم برای تمام rهای بزرگتر یا مساوی صفر برقرار است.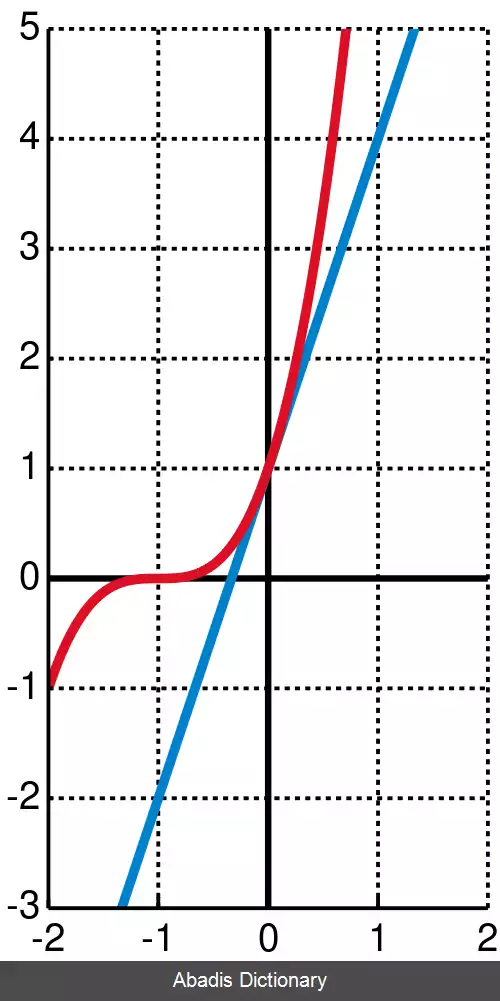
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین نابرابری بیان می کند که برای هر عدد صحیح مانند r که r ≥ 0 و هر عدد حقیقی مانند x که x ≥ −1 داریم:
اگر r زوج باشد آنگاه نابرابری برای تمام اعداد حقیقی x برقرار است.
از نابرابری برنولی معمولاً به عنوان یک پله مهم در اثبات دیگر نابرابری ها در ریاضیات استفاده می شود. خود این نابرابری نیز را می توان به کمک استقرای ریاضی اثبات کرد.
برای r = 0، ( 1 + x ) 0 ≥ 1 + 0 x هم ارز با 1 ≤ 1 می باشد که صحیح است.
حال فرض کنید حکم برای r = k ( k عددی مثبت ) برقرار است. داریم:
و از آنجا:
اما از آنجایی که kx2 ≥ 0 داریم:
در نتیجه:
یعنی حکم برای r = k + 1 برقرار است.
بنابراین با اسقراء نتیجه می گیریم که حکم برای تمام rهای بزرگتر یا مساوی صفر برقرار است.

wiki: نابرابری برنولی
