معادله دیفرانسیل ( به انگلیسی: Differential Equation ) در ریاضیات، معادله ای است که یک یا چند تابع مجهول و مشتقات آنها را به هم مرتبط می کند. [ ۱] عموماً در کاربردها، توابع کمیت های فیزیکی را نشان می دهند، مشتق ها نرخ تغییر آن ها را نشان می دهند، و معادله دیفرانسیل رابطه بین این دو را تعریف می کند. چنین روابطی بسیار رایج است، و به همین دلیل معادلات دیفرانسیل نقش برجسته ای در بسیاری از رشته ها از جمله مهندسی، فیزیک، اقتصاد و زیست شناسی دارند.
مطالعه معادلات دیفرانسیل عمدتاً شامل مطالعه جواب های آنها ( مجموعه توابعی که هر معادله را برآورده می کند ) و خواص جواب های آنها است. فقط معادلات دیفرانسیل ساده با فرمول های صریح قابل حل هستند. با این حال، امکان تعیین بسیاری از خواص جواب های یک معادله دیفرانسیل معین بدون محاسبه دقیق آنها وجود دارد.
اغلب هنگامی که یک عبارت فرم بسته برای جواب در دسترس نیست، می توان با استفاده از رایانه به صورت عددی جواب ها را تخمین زد. تئوری سیستم های دینامیکی بر تحلیل کیفی سیستم هایی که با معادلات دیفرانسیل توصیف شده اند، تأکید می کند، در حالی که روش های عددی زیادی برای تعیین راه حل ها با درجه ای از دقت معین توسعه داده شده اند.
معادلات دیفرانسیل با اختراع حساب دیفرانسیل و انتگرال توسط آیزاک نیوتن و گوتفرید لایبنیتس به وجود آمد. نیوتن در فصل ۲ کتاب خودMethodus fluxionum et Serierum Infinitarum، در سال ۱۶۷۱ سه نوع معادله دیفرانسیل را فهرست کرد:
d y d x = f ( x ) d y d x = f ( x , y ) x 1 ∂ y ∂ x 1 + x 2 ∂ y ∂ x 2 = y
در تمام این موارد، y یک تابع مجهول از x ( یا از x1 و x2 ) ، و f یک تابع معین است.
او این مثال ها و نمونه های دیگر را با استفاده از سری های بی نهایت حل می کند و در مورد منحصربه فرد نبودن جواب ها بحث می کند.
ژاکوب برنولی در سال ۱۶۹۵ میلادی معادله دیفرانسیل برنولی را پیشنهاد کرد. [ ۲] این معادله یک معادله دیفرانسیل معمولی با شکل زیر است:
y ′ + P ( x ) y = Q ( x ) y n
که سال بعد لایبنیتس با ساده کردن آن جواب هایی برای آن به دست آورد. [ ۳]
از نظر تاریخی، مسئله سیم ارتعاشی مانند یک ساز موسیقی توسط ژان لو رون دالامبر، لئونارد اویلر، دانیل برنولی و ژوزف لوئی لاگرانژ مورد مطالعه قرار گرفت. [ ۴] [ ۵] [ ۶] [ ۷] در سال ۱۷۴۶، دالامبر معادله موج یک بعدی را کشف کرد و در عرض ده سال اویلر معادله موج سه بعدی را کشف کرد. [ ۸]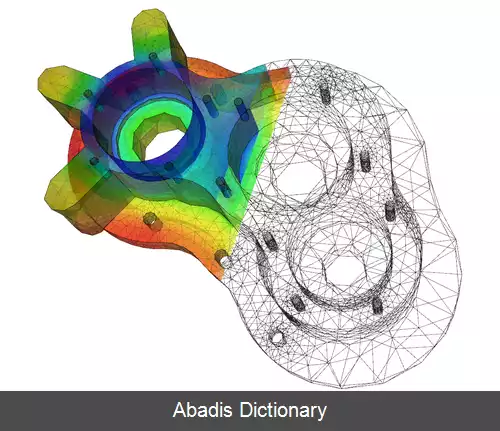

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمطالعه معادلات دیفرانسیل عمدتاً شامل مطالعه جواب های آنها ( مجموعه توابعی که هر معادله را برآورده می کند ) و خواص جواب های آنها است. فقط معادلات دیفرانسیل ساده با فرمول های صریح قابل حل هستند. با این حال، امکان تعیین بسیاری از خواص جواب های یک معادله دیفرانسیل معین بدون محاسبه دقیق آنها وجود دارد.
اغلب هنگامی که یک عبارت فرم بسته برای جواب در دسترس نیست، می توان با استفاده از رایانه به صورت عددی جواب ها را تخمین زد. تئوری سیستم های دینامیکی بر تحلیل کیفی سیستم هایی که با معادلات دیفرانسیل توصیف شده اند، تأکید می کند، در حالی که روش های عددی زیادی برای تعیین راه حل ها با درجه ای از دقت معین توسعه داده شده اند.
معادلات دیفرانسیل با اختراع حساب دیفرانسیل و انتگرال توسط آیزاک نیوتن و گوتفرید لایبنیتس به وجود آمد. نیوتن در فصل ۲ کتاب خودMethodus fluxionum et Serierum Infinitarum، در سال ۱۶۷۱ سه نوع معادله دیفرانسیل را فهرست کرد:
d y d x = f ( x ) d y d x = f ( x , y ) x 1 ∂ y ∂ x 1 + x 2 ∂ y ∂ x 2 = y
در تمام این موارد، y یک تابع مجهول از x ( یا از x1 و x2 ) ، و f یک تابع معین است.
او این مثال ها و نمونه های دیگر را با استفاده از سری های بی نهایت حل می کند و در مورد منحصربه فرد نبودن جواب ها بحث می کند.
ژاکوب برنولی در سال ۱۶۹۵ میلادی معادله دیفرانسیل برنولی را پیشنهاد کرد. [ ۲] این معادله یک معادله دیفرانسیل معمولی با شکل زیر است:
y ′ + P ( x ) y = Q ( x ) y n
که سال بعد لایبنیتس با ساده کردن آن جواب هایی برای آن به دست آورد. [ ۳]
از نظر تاریخی، مسئله سیم ارتعاشی مانند یک ساز موسیقی توسط ژان لو رون دالامبر، لئونارد اویلر، دانیل برنولی و ژوزف لوئی لاگرانژ مورد مطالعه قرار گرفت. [ ۴] [ ۵] [ ۶] [ ۷] در سال ۱۷۴۶، دالامبر معادله موج یک بعدی را کشف کرد و در عرض ده سال اویلر معادله موج سه بعدی را کشف کرد. [ ۸]






wiki: معادله دیفرانسیل
