معادلات ماکسوِل، معادله های دیفرانسیل با مشتقات جزئی هستند که به همراه قانون نیروی لورنتس، مبانی الکترومغناطیس کلاسیک، اپتیک کلاسیک، و مدارهای الکتریکی را تشکیل می دهند. این معادلات، مدل ریاضی فناوری های الکتریکی، اپتیکی، و رادیویی مانند تولید توان الکتریکی، موتورهای الکتریکی، مخابرات بی سیم، رادار، عدسی ها، و . . . را ارائه می کنند. معادلات ماکسول، چگونگی تولید شدن میدان های الکتریکی و مغناطیسی را توسط بارها و جریان های الکتریکی، و نیز تولید شدن یکی از این میدان ها با تغییر میدان دیگر را توصیف می کنند.
این معادله ها اولین بار توسط فیزیکدان اسکاتلندی جیمز کلارک ماکسول فرمول بندی شده اند. انواع فرمول بندی برای این معادله ها می توان ارائه داد. خود ماکسول این معادلات را در قالب هشت معادله ارائه کرده بود، ولی مشهورترین فرمول بندی را اُلیوِر هِوی ساید ( Heaviside ) ارائه کرد که دو فرم دیفرانسیلی و انتگرالی دارد.
فرم هوی ساید این معادله ها عبارت هستند از:
در اینجا ρ چگالی بار الکتریکی، J چگالی جریان الکتریکی، E شدت میدان الکتریکی، B چگالی شار مغناطیسی و D و H میدانهایی هستند که توسط چگالی قطبش الکتریکی و مغناطیسی ( به ترتیب P و M ) در ماده تعریف می شوند. در صورتی که ماده خطی باشد:
و برای این دو میدان به دست می آوریم:
فرم تنسوری چهاربعدی این معادلات این گونه است:
معادله دوم به اتحاد بیانکی ( Bianchi ) مشهور است.
معادلات ماکسول به افتخار فیزیکدان و ریاضیدان اسکاتلندی جیمز کلارک ماکسوِل نامگذاری شده است، زیرا در شکل اولیه، آن ها همگی در مقاله ای چهار بخشی از سوی او در میان سال های ۱۸۶۱ و ۱۸۶۲ منتشر شده است . فرم ریاضی قانون نیروی لورنتس نیز در این مقاله ظاهر شد . این معادلات انتشار امواج در خلاء با یک سرعت ثابت را توصیف می کنند. ماکسول همچنین نشان داد که این سرعت هم اندازه سرعت نور است و به درستی حدس زد که نور مانند امواج رادیویی و اشعه X، گونه ای از تابش الکترومغناطیسی و در محدوده طول موج های خاص است. معادلات ماکسول توصیف می کنند که میدان های الکتریکی و مغناطیسی چگونه تولید می شوند و با بار و جریان در تغییر هستند. نوشتن معادلات ماکسول به اشکال دیگر که هنوز هم "معادلات ماکسول" نامیده می شوند اغلب مفید است. در مکانیک کوانتوم، نسخه ای که بر اساس پتانسیل های الکتریکی و مغناطیسی هستند ترجیح داده می شود. از آنجا که معادلات ماکسول دلالت بر سرعت ثابت نور دارند، آن ها مدت ها معتقد بودند که فقط برای یک ناظر ساکن با توجه به فرض «اِتِر» معتبرند. اینشتین، در تئوری نسبیت خاص خود نظریه ای به جای معادلات ماکسول داد که برای ناظر دلخواه ( ساکن و متحرک ) معتبر بود ، و نشان داد که این مفاهیم از نظر فیزیکی مستقل از فضا و زمان ناظر است. با این حال، از اواسط قرن ۲۰ مشخص شده بود که معادلات ماکسول قوانین دقیق جهانی نیستند اما تقریب دقیق تر از نظریه اساسی الکترودینامیک کوانتومی هستند.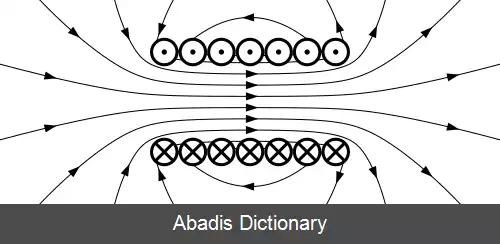



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین معادله ها اولین بار توسط فیزیکدان اسکاتلندی جیمز کلارک ماکسول فرمول بندی شده اند. انواع فرمول بندی برای این معادله ها می توان ارائه داد. خود ماکسول این معادلات را در قالب هشت معادله ارائه کرده بود، ولی مشهورترین فرمول بندی را اُلیوِر هِوی ساید ( Heaviside ) ارائه کرد که دو فرم دیفرانسیلی و انتگرالی دارد.
فرم هوی ساید این معادله ها عبارت هستند از:
در اینجا ρ چگالی بار الکتریکی، J چگالی جریان الکتریکی، E شدت میدان الکتریکی، B چگالی شار مغناطیسی و D و H میدانهایی هستند که توسط چگالی قطبش الکتریکی و مغناطیسی ( به ترتیب P و M ) در ماده تعریف می شوند. در صورتی که ماده خطی باشد:
و برای این دو میدان به دست می آوریم:
فرم تنسوری چهاربعدی این معادلات این گونه است:
معادله دوم به اتحاد بیانکی ( Bianchi ) مشهور است.
معادلات ماکسول به افتخار فیزیکدان و ریاضیدان اسکاتلندی جیمز کلارک ماکسوِل نامگذاری شده است، زیرا در شکل اولیه، آن ها همگی در مقاله ای چهار بخشی از سوی او در میان سال های ۱۸۶۱ و ۱۸۶۲ منتشر شده است . فرم ریاضی قانون نیروی لورنتس نیز در این مقاله ظاهر شد . این معادلات انتشار امواج در خلاء با یک سرعت ثابت را توصیف می کنند. ماکسول همچنین نشان داد که این سرعت هم اندازه سرعت نور است و به درستی حدس زد که نور مانند امواج رادیویی و اشعه X، گونه ای از تابش الکترومغناطیسی و در محدوده طول موج های خاص است. معادلات ماکسول توصیف می کنند که میدان های الکتریکی و مغناطیسی چگونه تولید می شوند و با بار و جریان در تغییر هستند. نوشتن معادلات ماکسول به اشکال دیگر که هنوز هم "معادلات ماکسول" نامیده می شوند اغلب مفید است. در مکانیک کوانتوم، نسخه ای که بر اساس پتانسیل های الکتریکی و مغناطیسی هستند ترجیح داده می شود. از آنجا که معادلات ماکسول دلالت بر سرعت ثابت نور دارند، آن ها مدت ها معتقد بودند که فقط برای یک ناظر ساکن با توجه به فرض «اِتِر» معتبرند. اینشتین، در تئوری نسبیت خاص خود نظریه ای به جای معادلات ماکسول داد که برای ناظر دلخواه ( ساکن و متحرک ) معتبر بود ، و نشان داد که این مفاهیم از نظر فیزیکی مستقل از فضا و زمان ناظر است. با این حال، از اواسط قرن ۲۰ مشخص شده بود که معادلات ماکسول قوانین دقیق جهانی نیستند اما تقریب دقیق تر از نظریه اساسی الکترودینامیک کوانتومی هستند.




wiki: معادلات ماکسول
