معادلات لاندن توسط برادران فریتز لاندن و هاینز لاندن در سال ۱۹۳۵ توسعه یافتند[ ۱] که مربوط به جریان در میدانهای الکترومغناطیسی در اطراف یک ابررسانا است. مسلماً ساده ترین توصیف معنی دار پدیده ابررسانایی است. [ ۲] [ ۳] [ ۴] عمده پیروزی معادلات توانایی برای توضیح اثر مایسنر است[ ۵] جایی که مواد به طور نمایی تمام میدان های مغناطیسی داخلی را از ماده به بیرون می فرستند وقتی که ماده از آستانه ابررسانی عبور کرد.
دو معادله لاندن برای بیان میدان های قابل اندازه گیری بیان می شوند:
در اینجا j s چگالی جریان ابررسانا است، E و B به ترتیب میدانهای الکتریکی و مغناطیسی در داخل ابررسانا هستند، e یک الکترون و پروتون است، m جرم الکترون و n s یک ثابت پدیدارشناسی است که مرتبط با تراکم تعداد حامل های ابررساناست. [ ۶] در سراسر این مقاله یکای SI استفاده می شوند.
از سوی دیگر اگر کسی مایل به انتزاعی تر کردن معادلات باشد، هر دو عبارات فوق می تواند به شکل تمیز و یکسان «معادله لاندن» و با استفاده از پتانسیل برداری A نوشته شود:[ ۷]
آخرین معادله تنها نقطه ضعفی که دارد این است که به طور پیمانه ای ناوردا نیست. اما تنها وقتی صحیح است که در پیمانه کولونی باشد که در آن دیورژانس A صفر است. [ ۸] این معادله برای میدان های مغناطیسی به آرامی در فضا تغییر می کنند صحیح است.
اگر دومین معادله لاندان را بگیرم قانون آمپر را روی آن استفاده کنیم، خواهیم داشت[ ۹]
سپس نتیجه معادله دیفرانسیل
بنابراین معادلات لاندن حاکی از خصیصه طولی است که میدان مغناطیسی خارجی به طور نمایی سرکوب می شود که این مقدار عمق نفوذ لاندن نام دارد.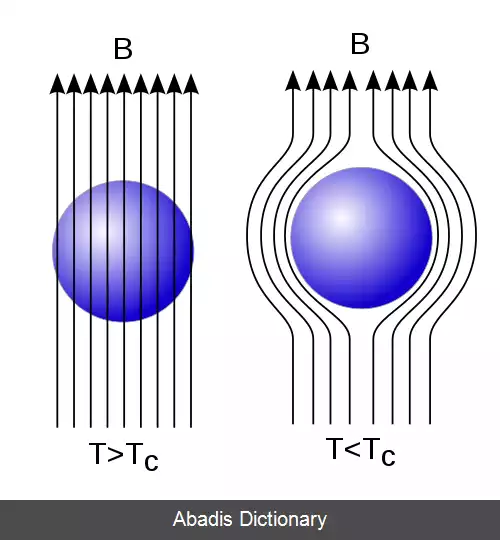
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدو معادله لاندن برای بیان میدان های قابل اندازه گیری بیان می شوند:
در اینجا j s چگالی جریان ابررسانا است، E و B به ترتیب میدانهای الکتریکی و مغناطیسی در داخل ابررسانا هستند، e یک الکترون و پروتون است، m جرم الکترون و n s یک ثابت پدیدارشناسی است که مرتبط با تراکم تعداد حامل های ابررساناست. [ ۶] در سراسر این مقاله یکای SI استفاده می شوند.
از سوی دیگر اگر کسی مایل به انتزاعی تر کردن معادلات باشد، هر دو عبارات فوق می تواند به شکل تمیز و یکسان «معادله لاندن» و با استفاده از پتانسیل برداری A نوشته شود:[ ۷]
آخرین معادله تنها نقطه ضعفی که دارد این است که به طور پیمانه ای ناوردا نیست. اما تنها وقتی صحیح است که در پیمانه کولونی باشد که در آن دیورژانس A صفر است. [ ۸] این معادله برای میدان های مغناطیسی به آرامی در فضا تغییر می کنند صحیح است.
اگر دومین معادله لاندان را بگیرم قانون آمپر را روی آن استفاده کنیم، خواهیم داشت[ ۹]
سپس نتیجه معادله دیفرانسیل
بنابراین معادلات لاندن حاکی از خصیصه طولی است که میدان مغناطیسی خارجی به طور نمایی سرکوب می شود که این مقدار عمق نفوذ لاندن نام دارد.


wiki: معادلات لاندن
