مشتق دوم یا مشتق مرتبه دو، مشتقِ مشتق تابع f می باشد. به طور کلی، مشتق دوم دربارهٔ چگونگی نرخ تغییرات یک کمیت است. برای مثال، مشتق دوم معادله مکان یک وسیله نقلیه، شتاب لحظه ای آن را نتیجه می دهد.
در نمودار یک تابع، مشتق دوم انحنا یا تقعر یک تابع را مشخص می کند. اگر مشتق دوم یک تابع در بازه ای مثبت باشد تقعر منحنی رو به بالا، اگر مشتق دوم منفی باشد تقعر رو به پایین و اگر مشتق دوم صفر باشد تابع در آن بازه تقعری ندارد.
d 2 d x 2 = d d x d d x = d d x = n d d x = n ( n − 1 ) x n − 2 .
مشتق دوم تابع f ( x ) را با نماد f ″ ( x ) نشان می دهند.
هنگامی که با استفاده از نماد لایبنیتس برای مشتقات، مشتق دوم یک Y متغیر وابسته، با توجه به متغیر x مستقل نوشته می شود:
این نماد از فرمول زیر بدست آمده است:
با توجه به تابع
مشتق تابع f می شود:
و مشتق تابع f' می شود:
در واقع برای بدست آمدن مشتق دوم باید از مشتق اول، یا ( از تابع اصلی دوبار ) مشتق گرفت.
اگر مشتق دوم تابع f مثبت باشد تقعر منحنی رو به بالا می باشد ( خط مماس بر منحنی زیر نمودار تابع محدب قرار می گیرد ) و اگر مشتق دوم تابع f منفی باشد تقعر منحنی رو به پایین می باشد ( خط مماس بر منحنی در بالای نمودار تابع کاو قرار می گیرد )
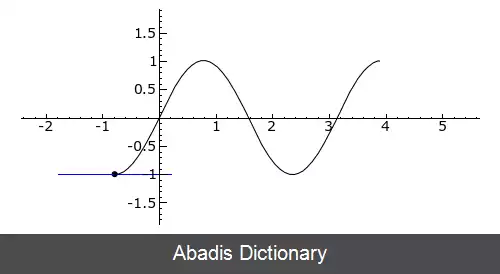
نقطهٔ عطف، نقطه ای بر روی یک خم است که انحنای آن خم در آن نقطه تغییر جهت می دهد. در واقع در نقطهٔ عطف جهت تقعر عوض می شود. به عبارت دیگر علامت مشتق دوم یک تابع، قبل و بعد از نقطهٔ عطفش بر روی تابع تغییر می کند. ( مثبت به منفی یا بالعکس )
برای پیدا کردن نقاط اکسترمم نسبی تابع می توان از آزمون مشتق دوم استفاده کرد:
• اگر f ′ ′ ( x ) < 0 {\displaystyle \ f^{\prime \prime } ( x ) < 0} باشد آنگاه f {\displaystyle \ f} در آن نقطه ماکسیمم نسبی است.
• اگر f ′ ′ ( x ) > 0 {\displaystyle \ f^{\prime \prime } ( x ) > 0} باشد آنگاه f {\displaystyle \ f} در آن نقطه مینیمم نسبی است.
• اگر f ′ ′ ( x ) = 0 {\displaystyle \ f^{\prime \prime } ( x ) =0} باشد آنگاه آزمون مشتق دوم پاسخی ندارد و باید به سراغ آزمون مشتق اول رفت.
این حد مشتق متقارن دوم است. توجه داشته باشید که مشتق متقارن دوم ممکن است وجود داشته حتی زمانی که ( طبق معمول ) مشتق دوم وجود نداشته باشد. در سمت راست به عنوان خارج قسمت تفاوت نوشته شده است: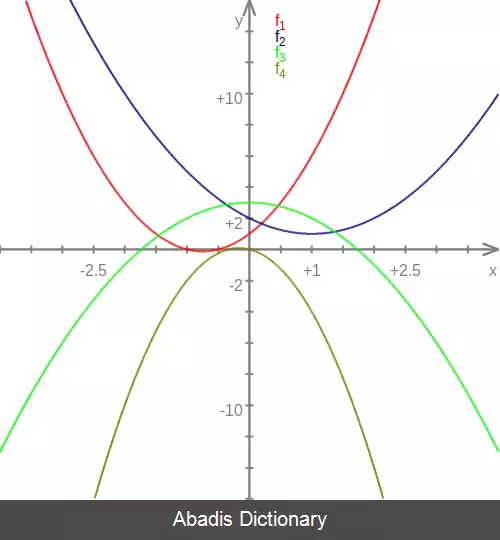
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر نمودار یک تابع، مشتق دوم انحنا یا تقعر یک تابع را مشخص می کند. اگر مشتق دوم یک تابع در بازه ای مثبت باشد تقعر منحنی رو به بالا، اگر مشتق دوم منفی باشد تقعر رو به پایین و اگر مشتق دوم صفر باشد تابع در آن بازه تقعری ندارد.
d 2 d x 2 = d d x d d x = d d x = n d d x = n ( n − 1 ) x n − 2 .
مشتق دوم تابع f ( x ) را با نماد f ″ ( x ) نشان می دهند.
هنگامی که با استفاده از نماد لایبنیتس برای مشتقات، مشتق دوم یک Y متغیر وابسته، با توجه به متغیر x مستقل نوشته می شود:
این نماد از فرمول زیر بدست آمده است:
با توجه به تابع
مشتق تابع f می شود:
و مشتق تابع f' می شود:
در واقع برای بدست آمدن مشتق دوم باید از مشتق اول، یا ( از تابع اصلی دوبار ) مشتق گرفت.
اگر مشتق دوم تابع f مثبت باشد تقعر منحنی رو به بالا می باشد ( خط مماس بر منحنی زیر نمودار تابع محدب قرار می گیرد ) و اگر مشتق دوم تابع f منفی باشد تقعر منحنی رو به پایین می باشد ( خط مماس بر منحنی در بالای نمودار تابع کاو قرار می گیرد )
نقطهٔ عطف، نقطه ای بر روی یک خم است که انحنای آن خم در آن نقطه تغییر جهت می دهد. در واقع در نقطهٔ عطف جهت تقعر عوض می شود. به عبارت دیگر علامت مشتق دوم یک تابع، قبل و بعد از نقطهٔ عطفش بر روی تابع تغییر می کند. ( مثبت به منفی یا بالعکس )
برای پیدا کردن نقاط اکسترمم نسبی تابع می توان از آزمون مشتق دوم استفاده کرد:
• اگر f ′ ′ ( x ) < 0 {\displaystyle \ f^{\prime \prime } ( x ) < 0} باشد آنگاه f {\displaystyle \ f} در آن نقطه ماکسیمم نسبی است.
• اگر f ′ ′ ( x ) > 0 {\displaystyle \ f^{\prime \prime } ( x ) > 0} باشد آنگاه f {\displaystyle \ f} در آن نقطه مینیمم نسبی است.
• اگر f ′ ′ ( x ) = 0 {\displaystyle \ f^{\prime \prime } ( x ) =0} باشد آنگاه آزمون مشتق دوم پاسخی ندارد و باید به سراغ آزمون مشتق اول رفت.
این حد مشتق متقارن دوم است. توجه داشته باشید که مشتق متقارن دوم ممکن است وجود داشته حتی زمانی که ( طبق معمول ) مشتق دوم وجود نداشته باشد. در سمت راست به عنوان خارج قسمت تفاوت نوشته شده است:


wiki: مشتق دوم
