مسئله حل نشده در ریاضیات:
( مسائل حل نشده بیشتر در ریاضیات )
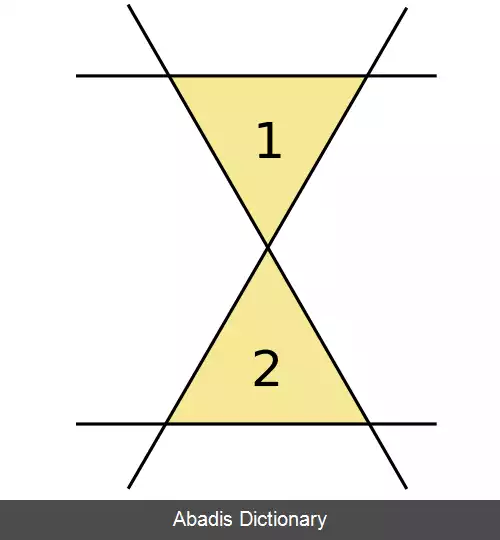
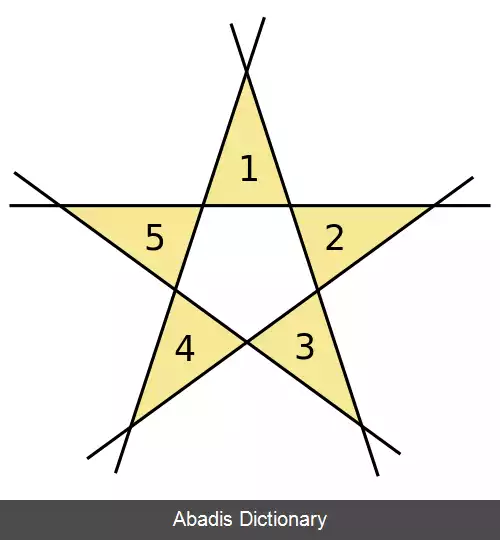
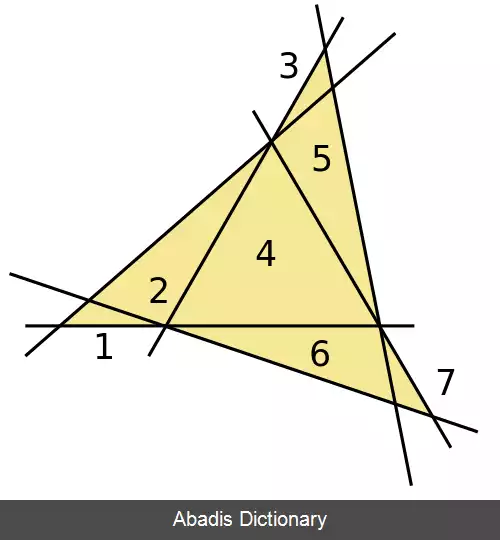
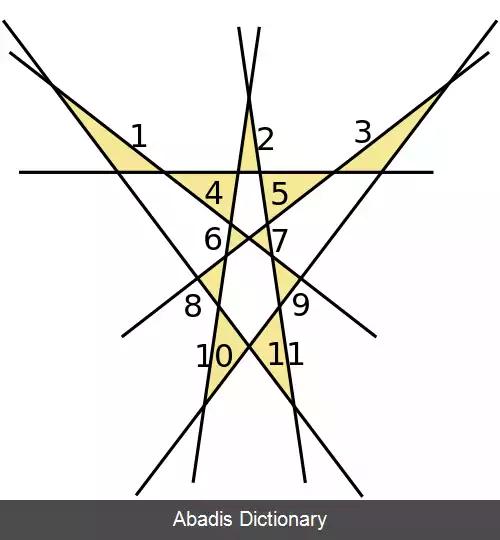
مسئله مثلث فوجیمورا ( یا مثلث کوبون ) یک مسئله حل نشده در هندسه گسسته است که اولین بار توسط کوبون فوجیمورا مطرح شده است. این مسئله بزرگترین عدد N ( k ) از مثلث های غیر همپوشان را می خواهد که اضلاعشان با استفاده از چینش k خط راست در صفحه به وجود آمده اند. مسائل مشابه دیگری از این مسئله به جای صفحه اقلیدسی، صفحه تصویری ( در هندسه تصویری ) را در نظر می گیرند و می خواهند که مثلث ها هیچ خط دیگری را به جز خطوط تشکیل دهنده شان قطع نکنند. [ ۱]
سابورو تامورا ثابت کرد که بزرگترین عدد صحیح که بزرگ تر از k ( k− 2 ) /3 نباشد، حد بالایی را در حداکثر تعداد مثلث های غیر همپوشان با چینش k خط به دست می دهد. [ ۲] در سال ۲۰۰۷، با اثبات اینکه حد بالایی تامورا برای هیچ k همنهشت با ۰ و ۲ ( به پیمانه ۶ ) به دست نمی آمد، حد بالایی محدودتری توسط یوهانس بادر و ژیل کلمان پیدا شد. [ ۳] پس برای این دو حالت حداکثر تعداد مثلث ها یکی کمتر از حد بالایی تامورا است. راه حل های کامل ( راه حل های مثلث فوجیمورا با حداکثر تعداد مثلث ) برای k = ۳، ۴، ۵، ۶، ۷، ۸، ۹، ۱۳، ۱۷ شناخته شده است. [ ۴] برای k = ۱۰، ۱۱، ۱۲، بهترین راه حل های شناخته شده یکی کمتر از حد بالایی است.
بر اساس اثبات کلمان و بادر، [ ۳] راه حل ها برای k> ۲ با مقادیر زیر محدود شده اند
با استفاده از یک راه حل کامل با k0> ۳ خط، راه حل های دیگر مثلث فوجیمورا می تواند برای تمام مقادیر ki که در آن
با استفاده از روش دی. فورج و جی. ال. رامیرز آلفونسین به دست بیاید. [ ۱] [ ۵] به عنوان مثال، به ازای k0 = ۵ این راه حل منجر به یافتن حداکثر تعداد مثلث های غیر همپوشان برای k = ۵٬۹٬۱۷٬۳۳٬۶۵ می شود.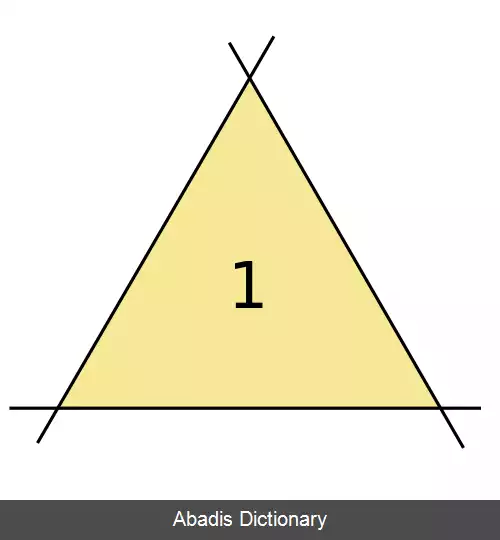

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف( مسائل حل نشده بیشتر در ریاضیات )
مسئله مثلث فوجیمورا ( یا مثلث کوبون ) یک مسئله حل نشده در هندسه گسسته است که اولین بار توسط کوبون فوجیمورا مطرح شده است. این مسئله بزرگترین عدد N ( k ) از مثلث های غیر همپوشان را می خواهد که اضلاعشان با استفاده از چینش k خط راست در صفحه به وجود آمده اند. مسائل مشابه دیگری از این مسئله به جای صفحه اقلیدسی، صفحه تصویری ( در هندسه تصویری ) را در نظر می گیرند و می خواهند که مثلث ها هیچ خط دیگری را به جز خطوط تشکیل دهنده شان قطع نکنند. [ ۱]
سابورو تامورا ثابت کرد که بزرگترین عدد صحیح که بزرگ تر از k ( k− 2 ) /3 نباشد، حد بالایی را در حداکثر تعداد مثلث های غیر همپوشان با چینش k خط به دست می دهد. [ ۲] در سال ۲۰۰۷، با اثبات اینکه حد بالایی تامورا برای هیچ k همنهشت با ۰ و ۲ ( به پیمانه ۶ ) به دست نمی آمد، حد بالایی محدودتری توسط یوهانس بادر و ژیل کلمان پیدا شد. [ ۳] پس برای این دو حالت حداکثر تعداد مثلث ها یکی کمتر از حد بالایی تامورا است. راه حل های کامل ( راه حل های مثلث فوجیمورا با حداکثر تعداد مثلث ) برای k = ۳، ۴، ۵، ۶، ۷، ۸، ۹، ۱۳، ۱۷ شناخته شده است. [ ۴] برای k = ۱۰، ۱۱، ۱۲، بهترین راه حل های شناخته شده یکی کمتر از حد بالایی است.
بر اساس اثبات کلمان و بادر، [ ۳] راه حل ها برای k> ۲ با مقادیر زیر محدود شده اند
با استفاده از یک راه حل کامل با k0> ۳ خط، راه حل های دیگر مثلث فوجیمورا می تواند برای تمام مقادیر ki که در آن
با استفاده از روش دی. فورج و جی. ال. رامیرز آلفونسین به دست بیاید. [ ۱] [ ۵] به عنوان مثال، به ازای k0 = ۵ این راه حل منجر به یافتن حداکثر تعداد مثلث های غیر همپوشان برای k = ۵٬۹٬۱۷٬۳۳٬۶۵ می شود.






wiki: مسئله مثلث فوجیمورا
