مسئله طولانی ترین مسیر ( به انگلیسی: longest path problem ) در تئوری گراف، مسئله یافتن یک مسیر ساده با با حداکثر طول در یک گراف خاص است.
یک مسیر زمانی ساده نامیده می شود که دارای رئوس تکراری نباشد. بر خلاف مسئله کوتاه ترین مسیر که کوتاهترین مسیر بین دو راس را به ما می دهد و در زمان چندجمله ای حل می شود، برای مسئله یافتن طولانی ترین مسیر زمان چندجمله ای وجود ندارد و جزء مسائل ان پی کامل ( NP - complete ) است. و به این معنی است که در زمان چندجمله ای نمی توان برای آن جواب پیدا کرد مگر اینکه P=NP باشد.
واضح است که اگر یک مسیر عمومی معین دارای مسیر Hamiltonian باشد، این مسیر Hamiltonian، بلندترین مسیر احتمالی است، زیرا همه رئوس احتمالی را طی می کند. برای حل مسئله Hamiltonian از یک الگوریتم طولانی ترین مسیر استفاده می کنیم، از این الگوریتم برای حل بلندترین مسیر در یک گراف با ورودی های یکسان و مجموعه k=|V| - ۱ استفاده می کنیم که |V| تعداد رئوس در گراف است.
اگر یک مسیر Hamiltonian در گراف وجود داشته باشد پس الگوریتم yes را برمی گرداند، زیرا مسیر Hamiltonian دارای طول معادل با1 - |V| است. بر عکس اگر الگوریتم دارای خروجی yes باشد، یک مسیر ساده با طول 1 - |V| در گراف وجود دارد. و چون طول آن |V| - 1 است می توان نتیجه گرفت که از همه رئوس گراف بدون تکرارگذشته است که همان مسیر Hamiltonian است. چون مسئله مسیر Hamiltonian یک مسئله ان پی کامل NP - complete است، این ساده سازی اثبات می کند که ان پی سخت ( NP - hard ) نیز است. برای اینکه تشان دهیم NP - complete است باید نشان دهیم NP است.
مسئله یافتن طولانی ترین مسیر را می توان به مسئله یافتن کوتاهترین مسیر کاهش ( reduction ) داد. ( گرچه ممکن است این گراف دارای دور با وزن منفی باشد ) اگر گراف ورودی برای مسئله بلندترین مسیر G باشد، کوتاهترین مسیر ساده بر روی گراف Hamiltonian خواهد بود که دقیقاً مشابه G است، اما وزن های لبه منفی می شود، و بلندترین مسیر بر روی G است. هر چند هر یک از دورها با وزن مثبت در گراف اصلی G منتهی به دورهایی با وزن منفی در گراف Hamiltonian خواهد شد. بنابراین یافتن کوتاه ترین مسیر ساده بر روی یک گراف با دورهایی با وزن منفی، نیز ان پی کاملاست. اگر G حاوی هیچ دوری نباشد، پس Hamiltonian هیچ دوری با وزن منفی نخواهد داشت و هر یک از الگوریتم های یافتن کوتاه ترین مسیر اکنون می تواند بر روی Hamiltonian اجرا شوند تا مسئله اصلی در زمان چندجمله ای حل شود. بنابراین مسئله بلندترین مسیر بر روی گراف های بدون دور ساده است.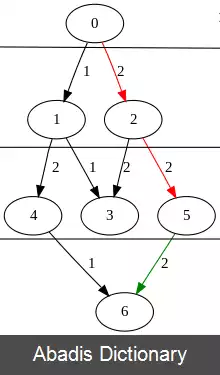
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک مسیر زمانی ساده نامیده می شود که دارای رئوس تکراری نباشد. بر خلاف مسئله کوتاه ترین مسیر که کوتاهترین مسیر بین دو راس را به ما می دهد و در زمان چندجمله ای حل می شود، برای مسئله یافتن طولانی ترین مسیر زمان چندجمله ای وجود ندارد و جزء مسائل ان پی کامل ( NP - complete ) است. و به این معنی است که در زمان چندجمله ای نمی توان برای آن جواب پیدا کرد مگر اینکه P=NP باشد.
واضح است که اگر یک مسیر عمومی معین دارای مسیر Hamiltonian باشد، این مسیر Hamiltonian، بلندترین مسیر احتمالی است، زیرا همه رئوس احتمالی را طی می کند. برای حل مسئله Hamiltonian از یک الگوریتم طولانی ترین مسیر استفاده می کنیم، از این الگوریتم برای حل بلندترین مسیر در یک گراف با ورودی های یکسان و مجموعه k=|V| - ۱ استفاده می کنیم که |V| تعداد رئوس در گراف است.
اگر یک مسیر Hamiltonian در گراف وجود داشته باشد پس الگوریتم yes را برمی گرداند، زیرا مسیر Hamiltonian دارای طول معادل با1 - |V| است. بر عکس اگر الگوریتم دارای خروجی yes باشد، یک مسیر ساده با طول 1 - |V| در گراف وجود دارد. و چون طول آن |V| - 1 است می توان نتیجه گرفت که از همه رئوس گراف بدون تکرارگذشته است که همان مسیر Hamiltonian است. چون مسئله مسیر Hamiltonian یک مسئله ان پی کامل NP - complete است، این ساده سازی اثبات می کند که ان پی سخت ( NP - hard ) نیز است. برای اینکه تشان دهیم NP - complete است باید نشان دهیم NP است.
مسئله یافتن طولانی ترین مسیر را می توان به مسئله یافتن کوتاهترین مسیر کاهش ( reduction ) داد. ( گرچه ممکن است این گراف دارای دور با وزن منفی باشد ) اگر گراف ورودی برای مسئله بلندترین مسیر G باشد، کوتاهترین مسیر ساده بر روی گراف Hamiltonian خواهد بود که دقیقاً مشابه G است، اما وزن های لبه منفی می شود، و بلندترین مسیر بر روی G است. هر چند هر یک از دورها با وزن مثبت در گراف اصلی G منتهی به دورهایی با وزن منفی در گراف Hamiltonian خواهد شد. بنابراین یافتن کوتاه ترین مسیر ساده بر روی یک گراف با دورهایی با وزن منفی، نیز ان پی کاملاست. اگر G حاوی هیچ دوری نباشد، پس Hamiltonian هیچ دوری با وزن منفی نخواهد داشت و هر یک از الگوریتم های یافتن کوتاه ترین مسیر اکنون می تواند بر روی Hamiltonian اجرا شوند تا مسئله اصلی در زمان چندجمله ای حل شود. بنابراین مسئله بلندترین مسیر بر روی گراف های بدون دور ساده است.

wiki: مسئله طولانی ترین مسیر
