در علم کامپیوتر مسئله تقسیم بندی به مسئله امکان تقسیم یک مجموعه با تکرار ( به انگلیسی: Multiset ) از اعداد طبیعی به دو زیرمجموعهٔ S1 و S2 گفته می شود به طوری که حاصل جمع اعداد این دو زیرمجموعه با هم برابر باشد. اگرچه این مسئله ان پی کامل است اما یک راه حل در زمان شبه چندجمله ای با استفاده از برنامه ریزی پویا برای آن وجود دارد. همچنین راه حل های اکتشافی ( به انگلیسی: heuristic ) برای حل بسیاری از نمونه های آن وجود دارد ( چه بهینه و چه تقریبی ) . به همین دلیل این مسئله به عنوان "ساده ترین مسئله سخت" شناخته شده است.
یک حالت بهینه سازی از این مسئله نیز وجود دارد که به تقسیم یک مجموعه با تکرار به دو زیرمجموعهٔ S1 و S2 می پردازد به نحوی که تفاوت حاصل جمع اعضای این دو زیر. مجموعه کمینه شود.
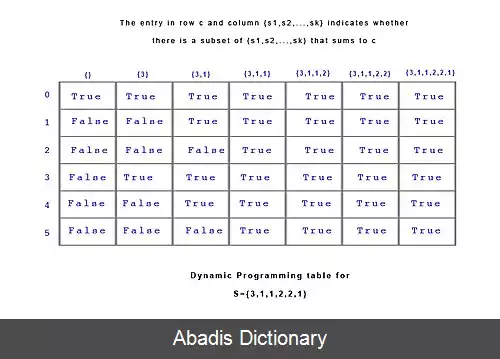
با داشتن مجموعه {S = {3, 1, 1, 2, 2, 1 یک راه حل ممکن برای مسئله تقسیم بندی زیرمجموعه های {S1 = {1, 1, 1, 2 و {S2 = {2, 3 می باشد که در هر دو حاصل جمع اعضا 5 است.
توجه کنید که این راه حل یکتا نیست زیرا {S1 = {3, 1, 1 و {S2 = {2, 2, 1 راه حل دیگری برای این مسئله می باشد.
در حالتی که اندازه مجموعه و نیز حاصل جمع اعداد داخل آن به قدری بزرگ نباشند که مشکلات ذخیره سازی به وجود آورند، این مسئله به وسیله برنامه ریزی پویا قابل حل خواهد بود.
فرض کنید ورودی الگوریتم به شکل زیر است:
S = x1, . . . , xn
متغیر N را مجموع تمام اعضای داخل S در نظر بگیرید. در ادامه الگوریتمی ارائه خواهیم داد که مشخص می کند آیا زیرمجموعه ای از S وجود دارد که حاصل جمع اعضای آن ⌊ N / 2 ⌋ شود یا خیر. اگر چنین زیرمجموعه ای وجود داشته باشد:
• اگر N زوج باشد، حاصل جمع سایر عضوهای S نیز ⌊ N / 2 ⌋ {\displaystyle \lfloor N/2\rfloor } خواهد بود.
• اگر N فرد باشد، حاصل جمع سایر عضوهای S برابر ⌈ N / 2 ⌉ {\displaystyle \lceil N/2\rceil } خواهد بود و این بهترین جواب ممکن است.
( p ( i, j را صحیح قرار می دهیم اگر زیرمجموعه ای از { x1, . . . , xj} وجود داشته باشد که حاصل جمع عضوهایش برابر i شود و در غیر این صورت آن را برابر "غلط" قرار می دهیم.
پس ( p ( ⌊ N / 2 ⌋ , n صحیح است اگر و تنها اگر یک زیرمجموعه از S وجود داشته باشد که حاصل جمع اعضای آن ⌊ N / 2 ⌋ باشد. پس هدف این الگوریتم محاسبه ( p ( ⌊ N / 2 ⌋ , n است. به توجه به این مطلب به رابطه بازگشتی زیر می رسیم: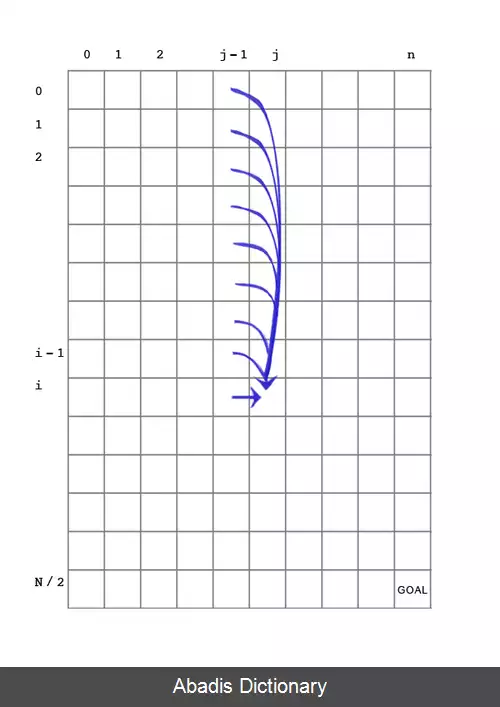
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک حالت بهینه سازی از این مسئله نیز وجود دارد که به تقسیم یک مجموعه با تکرار به دو زیرمجموعهٔ S1 و S2 می پردازد به نحوی که تفاوت حاصل جمع اعضای این دو زیر. مجموعه کمینه شود.
با داشتن مجموعه {S = {3, 1, 1, 2, 2, 1 یک راه حل ممکن برای مسئله تقسیم بندی زیرمجموعه های {S1 = {1, 1, 1, 2 و {S2 = {2, 3 می باشد که در هر دو حاصل جمع اعضا 5 است.
توجه کنید که این راه حل یکتا نیست زیرا {S1 = {3, 1, 1 و {S2 = {2, 2, 1 راه حل دیگری برای این مسئله می باشد.
در حالتی که اندازه مجموعه و نیز حاصل جمع اعداد داخل آن به قدری بزرگ نباشند که مشکلات ذخیره سازی به وجود آورند، این مسئله به وسیله برنامه ریزی پویا قابل حل خواهد بود.
فرض کنید ورودی الگوریتم به شکل زیر است:
S = x1, . . . , xn
متغیر N را مجموع تمام اعضای داخل S در نظر بگیرید. در ادامه الگوریتمی ارائه خواهیم داد که مشخص می کند آیا زیرمجموعه ای از S وجود دارد که حاصل جمع اعضای آن ⌊ N / 2 ⌋ شود یا خیر. اگر چنین زیرمجموعه ای وجود داشته باشد:
• اگر N زوج باشد، حاصل جمع سایر عضوهای S نیز ⌊ N / 2 ⌋ {\displaystyle \lfloor N/2\rfloor } خواهد بود.
• اگر N فرد باشد، حاصل جمع سایر عضوهای S برابر ⌈ N / 2 ⌉ {\displaystyle \lceil N/2\rceil } خواهد بود و این بهترین جواب ممکن است.
( p ( i, j را صحیح قرار می دهیم اگر زیرمجموعه ای از { x1, . . . , xj} وجود داشته باشد که حاصل جمع عضوهایش برابر i شود و در غیر این صورت آن را برابر "غلط" قرار می دهیم.
پس ( p ( ⌊ N / 2 ⌋ , n صحیح است اگر و تنها اگر یک زیرمجموعه از S وجود داشته باشد که حاصل جمع اعضای آن ⌊ N / 2 ⌋ باشد. پس هدف این الگوریتم محاسبه ( p ( ⌊ N / 2 ⌋ , n است. به توجه به این مطلب به رابطه بازگشتی زیر می رسیم:


wiki: مسئله تقسیم بندی
