به زبان صوری، مسئله تصمیم ( Decision problem ) در نظریهٔ محاسبات به مجموعه ای از سؤالات مربوط به هم اطلاق می شود، به طوری که هر یک از پرسش ها جواب بلی یا خیر داشته باشد. [ ۱]
در نظریه شمارش و همچنین پیچیدگی محاسباتی، مسئله تصمیم گیری، سؤالی با پاسخ بله یا خیر می باشد که به ورودی بستگی دارد. برای مثال در مسئله "با داشتن X و Y آیا X بر Y بخشپذیر است"یک مسئله تصمیم گیری است؛ که جواب آن می تواند بله یا خیر بر اساس مقادیر X و Y باشد. روشی که به شکل الگوریتم برای حل یک مسئله تصمیم گیری ارائه می شود فرایند تصمیم گیری برای آن مسئله نامیده می شود. فرایند تصمیم گیری برای مسئله"با داشتن X و Y آیا X بر Y بخشپذیر است؟"شامل گام های لازم برای مشخص کردن این است که آیا X بر Y تقسیم می شود یا خیر. الگوریتم به کار رفته در این مسئله تقسیم است، اگر باقی مانده صفر شود جواب مثبت است در غیر اینصورت خیر. به سؤالی که با الگوریتم قابل حل باشد تصمیم پذیر می گویند.
مسئله تصمیم گیری هر سؤال دلخواه بله یا خیر است که ورودی های محدود دارد. به همین خاطر، به صورت سنتی مسئله تصمیم گیری به شکل زیر تعریف می شود: مجموعه از ورودی ها که بازای آن ها خروجی مسئله «بله» می شود. این ورودی ها می توانند اعداد طبیعی باشند همچنین رشته های یک زبان که با نوعی کد گذاری خاص قابل تبدیل به اعداد طبیعی هستند. بنابرین به صورت غیررسمی، مسئله تصمیم گیری هم ارزبا مجموعه اعداد طبیعی در نظر گرفته می شود. برای ساده سازی تعریف رسمی، آن را به صورت زیر مجموعه از اعداد طبیعی بازگو می کنیم. بنابرین مسئله تصمیم گیری معادل این است که آیا عدد داده شده در زیر مجموعه وجود دارد یا نه؟
مسئله A تصمیم پذیر یا قابل حل نامیده می شود، اگر A مجموعه بازگشتی شمارا باشد ( یعنی بتوان به ازای متناهی عمل تصمیم گرفت که آیا عدد مورد نظر به مجموعه تعلق دارد یا نه؟ ) یک مسئله قسمتی تصمیم پذیر یا قابل اثبات نامیده می شود اگر الگوریتمی وجود داشته باشد که اعضا مجموعه مورد نظر را بشمارد، حتی اگر برای همیشه این کار ادامه یابد. به مسائل قابل اثبات یا دیگر مسائل تصمیم ناپذیر گویند.
یک نمونه کلاسیک از این نوع مسئله، مجموعه اعداد ا اول می باشد، از آنجا که به سادگی قابل تصمیم گیری است که آیا یک عدد طبیعی اول می باشد یا نه؟ ( با تقسیم کردن آن بر عوامل اول ) هرچند برای تشخیص اول بودن الگوریتم های کارآمد تری موجود است، وجود یک روش برای حل مسئله تصمیم گیری کافی است.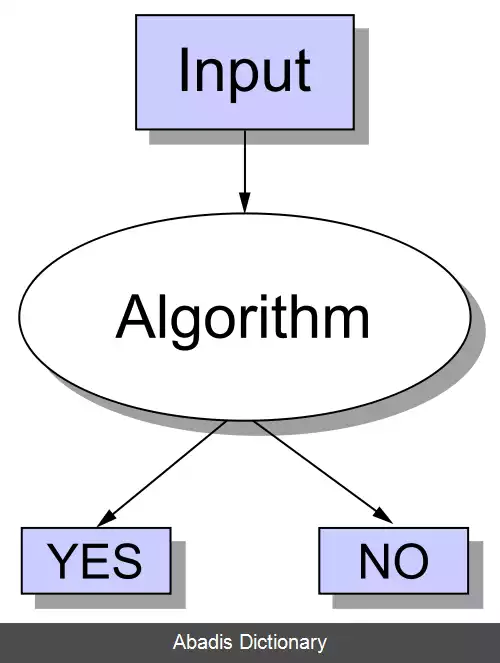
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر نظریه شمارش و همچنین پیچیدگی محاسباتی، مسئله تصمیم گیری، سؤالی با پاسخ بله یا خیر می باشد که به ورودی بستگی دارد. برای مثال در مسئله "با داشتن X و Y آیا X بر Y بخشپذیر است"یک مسئله تصمیم گیری است؛ که جواب آن می تواند بله یا خیر بر اساس مقادیر X و Y باشد. روشی که به شکل الگوریتم برای حل یک مسئله تصمیم گیری ارائه می شود فرایند تصمیم گیری برای آن مسئله نامیده می شود. فرایند تصمیم گیری برای مسئله"با داشتن X و Y آیا X بر Y بخشپذیر است؟"شامل گام های لازم برای مشخص کردن این است که آیا X بر Y تقسیم می شود یا خیر. الگوریتم به کار رفته در این مسئله تقسیم است، اگر باقی مانده صفر شود جواب مثبت است در غیر اینصورت خیر. به سؤالی که با الگوریتم قابل حل باشد تصمیم پذیر می گویند.
مسئله تصمیم گیری هر سؤال دلخواه بله یا خیر است که ورودی های محدود دارد. به همین خاطر، به صورت سنتی مسئله تصمیم گیری به شکل زیر تعریف می شود: مجموعه از ورودی ها که بازای آن ها خروجی مسئله «بله» می شود. این ورودی ها می توانند اعداد طبیعی باشند همچنین رشته های یک زبان که با نوعی کد گذاری خاص قابل تبدیل به اعداد طبیعی هستند. بنابرین به صورت غیررسمی، مسئله تصمیم گیری هم ارزبا مجموعه اعداد طبیعی در نظر گرفته می شود. برای ساده سازی تعریف رسمی، آن را به صورت زیر مجموعه از اعداد طبیعی بازگو می کنیم. بنابرین مسئله تصمیم گیری معادل این است که آیا عدد داده شده در زیر مجموعه وجود دارد یا نه؟
مسئله A تصمیم پذیر یا قابل حل نامیده می شود، اگر A مجموعه بازگشتی شمارا باشد ( یعنی بتوان به ازای متناهی عمل تصمیم گرفت که آیا عدد مورد نظر به مجموعه تعلق دارد یا نه؟ ) یک مسئله قسمتی تصمیم پذیر یا قابل اثبات نامیده می شود اگر الگوریتمی وجود داشته باشد که اعضا مجموعه مورد نظر را بشمارد، حتی اگر برای همیشه این کار ادامه یابد. به مسائل قابل اثبات یا دیگر مسائل تصمیم ناپذیر گویند.
یک نمونه کلاسیک از این نوع مسئله، مجموعه اعداد ا اول می باشد، از آنجا که به سادگی قابل تصمیم گیری است که آیا یک عدد طبیعی اول می باشد یا نه؟ ( با تقسیم کردن آن بر عوامل اول ) هرچند برای تشخیص اول بودن الگوریتم های کارآمد تری موجود است، وجود یک روش برای حل مسئله تصمیم گیری کافی است.

wiki: مسئله تصمیم
