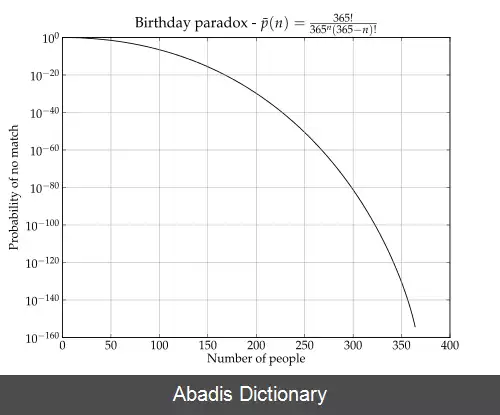
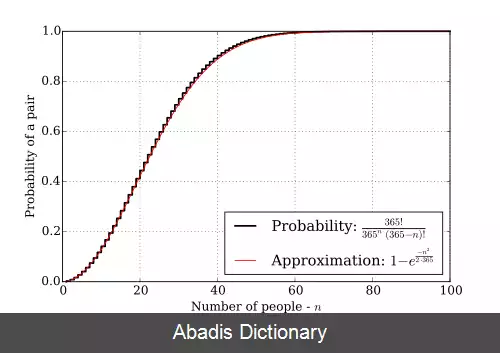
در تئوری احتمالات، مسئله تاریخ تولد یا پارادوکس تاریخ تولد به یافتن احتمال حضور بیش از دو نفر در مجموعهٔ تصادفی n نفره که تاریخ تولد یکسانی داشته باشند، مربوط است. طبق اصل لانه کبوتری این احتمال وقتی که تعداد افراد حاضر برابر با ۳۶۶ ( با فرض این که سال ۳۶۵ روز است، بدون در نظر سال کبیسه ) شود، مساوی ۱۰۰٪ می شود. اگرچه احتمال ۹۹٪ وقتی که تعداد افراد تنها برابر ۵۷ نفر است حاصل می شود. [ ۱] همچنین با احتمال ۵۰٪ حداقل دو نفر تولد یکسانی بین ۲۳ نفر دارند. این نتایج با این فرض به دست می آید که سال دارای ۳۶۵ روز ( یعنی با در نظر نگرفتن ۳۰ اسفند ) و احتمال تولد افراد در آن ها برابر هم باشد.
محاسبات ریاضی پشت این مسئله باعث ایجاد یک حمله رمزنگاری معروف به اسم حمله روز تولد شده است. این حمله بر اساس مدل احتمالی مسئله تاریخ تولد، پیچیدگی توابع درهم سازی را کاهش می دهد و باعث ساده شدن شکستن آن می شود.
مسئله روز تولد این سؤال را مطرح می کند که آیا درون یک گروه معین هیچ فردی وجود دارد که با یکی دیگر از افراد گروه تاریخ تولد مشابهی داشته باشد - نه شخص خاصی به طور مشخص. ( به قسمت «#هم تاریخ تولد با شما» در زیر نگاه کنید برای تحلیل این مسئله جایگزینی که کمتر جالب به نظر می رسد ) در مثالی که پیش از این مطرح شد، در لیستی شامل ۲۳ نفر، در مقایسه شانس اینکه تاریخ تولد نفر اول لیست با دیگران یکسان باشد ۲۲ است، برای نفر دوم لیست برابر با ۲۱، برای نفر سوم لیست برابر با ۲۰ و همین طور تا آخر. از این رو مجموع شانس ها برابر است با: ۲۲+۲۱+۲۱+. . . +۱ = ۲۵۳، بنابراین مقایسه هر فرد با تمام افراد دیگر ۲۵۳ شانس مجزا را به وجود می آورد ( ترکیب ) : در یک گروه ۲۳ نفری ( ۲۳¦۲ ) = ۲۳٫۲۲/۲=۲۵۳جفت وجود دارد. با فرض اینکه احتمال تمام روزهای تولد یکسان باشد، احتمال یک تاریخ تولد داده شده برای فردی که به طور تصادفی از بین جمع انتخاب شده ۱/۳۶۵ ( با نادیده گرفتن روز کبیسه، ۳۰ اسفند ) است. اگرچه زوج های یک گروه ۲۳ نفری از لحاظ آماری با ۲۵۳ زوجی که به طور مستقل انتخاب شده اند هم ارز نیستند، اگر یک گروه بر حسب تعداد زوج های آن سنجیده شود، پارادوکس تولد نسبت به زمانی که بر حسب افراد سنجیده شود، کم تر تعجب برانگیز خواهد بود.
مسئله مورد نظر، محاسبه احتمال تقریبی حضور حداقل دو نفر در اتاقی با حضور n نفر، با تاریخ تولد یکسان است. برای سادگی، تفاوت ها در توزیع، مانند سال کبیسه، دوقلوها، تغییرات روزهای هفته و تغییرات فصلی را نادیده بگیرید و فرض کنید ۳۶۵ تاریخ تولدی که امکان پذیرند، احتمال برابری داشته باشند. توزیع تاریخ تولدها در واقعیت یکنواخت نیست، زیرا تمام تاریخ ها احتمال برابری ندارند. اگر P ( A ) احتمال حضور حداقل ۲ نفر در یک اتاق با تاریخ تولدهای یکسان باشد، محاسبه P ( A’ ) ، یعنی احتمال نبود هیچ دو نفری که تولد یکسان داشته باشند می تواند آسان تر باشد؛ بنابراین، به این دلیل که P ( A ) و P ( A' ) تنها احتمالات ممکن و دو به دو ناسازگار هستند، P ( A' ) = ۱ − P ( A ) ) . برای احترام به راه حل های منتشر شدهٔ زیادی که نتیجه گرفته اند برای داشتن P ( A ) بیشتر از ۵۰٪ حضور ۲۳ نفر ضروری است، در زیر، برای محاسبه P ( A ) ، ۲۳ نفر به عنوان مثال در نظر گرفته می شود. وقتی رویدادها مستقل از یکدیگر باشند، احتمال کل رویدادهایی که اتفاق می افتند برابر است با ضرب احتمالات هر کدام از رویدادها؛ بنابراین اگر P ( A' ) به عنوان ۲۳ رویداد مستقل تعریف شود، می توان به این صورت آن را محاسبه کرد: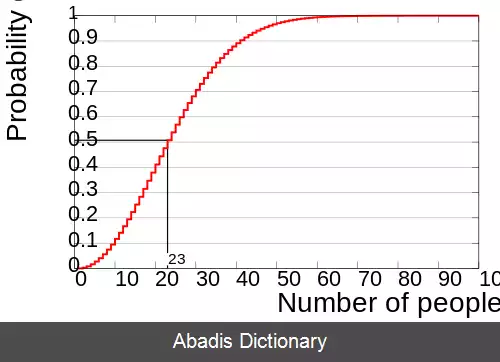
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمحاسبات ریاضی پشت این مسئله باعث ایجاد یک حمله رمزنگاری معروف به اسم حمله روز تولد شده است. این حمله بر اساس مدل احتمالی مسئله تاریخ تولد، پیچیدگی توابع درهم سازی را کاهش می دهد و باعث ساده شدن شکستن آن می شود.
مسئله روز تولد این سؤال را مطرح می کند که آیا درون یک گروه معین هیچ فردی وجود دارد که با یکی دیگر از افراد گروه تاریخ تولد مشابهی داشته باشد - نه شخص خاصی به طور مشخص. ( به قسمت «#هم تاریخ تولد با شما» در زیر نگاه کنید برای تحلیل این مسئله جایگزینی که کمتر جالب به نظر می رسد ) در مثالی که پیش از این مطرح شد، در لیستی شامل ۲۳ نفر، در مقایسه شانس اینکه تاریخ تولد نفر اول لیست با دیگران یکسان باشد ۲۲ است، برای نفر دوم لیست برابر با ۲۱، برای نفر سوم لیست برابر با ۲۰ و همین طور تا آخر. از این رو مجموع شانس ها برابر است با: ۲۲+۲۱+۲۱+. . . +۱ = ۲۵۳، بنابراین مقایسه هر فرد با تمام افراد دیگر ۲۵۳ شانس مجزا را به وجود می آورد ( ترکیب ) : در یک گروه ۲۳ نفری ( ۲۳¦۲ ) = ۲۳٫۲۲/۲=۲۵۳جفت وجود دارد. با فرض اینکه احتمال تمام روزهای تولد یکسان باشد، احتمال یک تاریخ تولد داده شده برای فردی که به طور تصادفی از بین جمع انتخاب شده ۱/۳۶۵ ( با نادیده گرفتن روز کبیسه، ۳۰ اسفند ) است. اگرچه زوج های یک گروه ۲۳ نفری از لحاظ آماری با ۲۵۳ زوجی که به طور مستقل انتخاب شده اند هم ارز نیستند، اگر یک گروه بر حسب تعداد زوج های آن سنجیده شود، پارادوکس تولد نسبت به زمانی که بر حسب افراد سنجیده شود، کم تر تعجب برانگیز خواهد بود.
مسئله مورد نظر، محاسبه احتمال تقریبی حضور حداقل دو نفر در اتاقی با حضور n نفر، با تاریخ تولد یکسان است. برای سادگی، تفاوت ها در توزیع، مانند سال کبیسه، دوقلوها، تغییرات روزهای هفته و تغییرات فصلی را نادیده بگیرید و فرض کنید ۳۶۵ تاریخ تولدی که امکان پذیرند، احتمال برابری داشته باشند. توزیع تاریخ تولدها در واقعیت یکنواخت نیست، زیرا تمام تاریخ ها احتمال برابری ندارند. اگر P ( A ) احتمال حضور حداقل ۲ نفر در یک اتاق با تاریخ تولدهای یکسان باشد، محاسبه P ( A’ ) ، یعنی احتمال نبود هیچ دو نفری که تولد یکسان داشته باشند می تواند آسان تر باشد؛ بنابراین، به این دلیل که P ( A ) و P ( A' ) تنها احتمالات ممکن و دو به دو ناسازگار هستند، P ( A' ) = ۱ − P ( A ) ) . برای احترام به راه حل های منتشر شدهٔ زیادی که نتیجه گرفته اند برای داشتن P ( A ) بیشتر از ۵۰٪ حضور ۲۳ نفر ضروری است، در زیر، برای محاسبه P ( A ) ، ۲۳ نفر به عنوان مثال در نظر گرفته می شود. وقتی رویدادها مستقل از یکدیگر باشند، احتمال کل رویدادهایی که اتفاق می افتند برابر است با ضرب احتمالات هر کدام از رویدادها؛ بنابراین اگر P ( A' ) به عنوان ۲۳ رویداد مستقل تعریف شود، می توان به این صورت آن را محاسبه کرد:




wiki: مسئله تاریخ تولد
