در شرایطی که عناصری که قرار است مرتب شوند دارای یک سری محدودیت های خاص یا شرایط خاص می باشند، می توان برای مرتب کردن آنها از روش هایی به غیر از روش ها یا الگوریتم های مرتب سازی مقایسه ای مانند :مرتب سازی ادغامی استفاده کرد و به الگوریتم های سریعتری از ( O ( n log n دست یافت. به دسته ای از این گونه مرتب سازی ها که بر پایهٔ یک سری شرایط خاص عناصر هستند و دارای پیچیدگی خطی هستند مرتب سازی خطی می گوییم. مرتب سازی های مقایسه ای الگوریتمی سریع تر از ( O ( n log n ندارند که این موضوع با کمک درخت تصمیم اثبات می شود.
انواع مرتب سازی های خطی عبارتند از مرتب سازی شمارشی، مرتب سازی سطلی، مرتب سازی مبنایی و BeadSort و BrustSort و PigeonholeSort و. . .
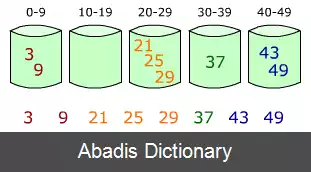
در این الگوریتم محدودیت اعمال شده روی داده این است که کلید تمامی عناصر باید اعداد صحیح بوده و بین 1 تا m قرار بگیرند که m یک عدد ثابت است و این الگوریتم با استفاده از آرایه ای از اعداده صحیح به طول m عناصر مورد نظر را مرتب می کند. به طور خلاصه الگوریتم به این صورت عمل می کند که تعداد دفعات ظاهر شدن هر عنصر در ورودی را با کمک آرایه گرفته شده حساب می کند و سپس با این اطلاعات از ابتدا شروع کرده و هر عنصر را به تعداد دفعات ظهورش در ورودی در خروجی قرار می دهد، و با توجه به اینکه این عمل را از 1 تا m انجام می دهد خروجی مرتب شده است. برای تشریح کامل الگوریتم به صفحه مرتب سازی شمارشی مراجعه کنید.
این الگوریتم مرتب سازی برای مرتب کردن اعدادی با طول ثابت به اندازهٔ k مورد استفاده قرار می گیرد و کاربرد دارد. البته بهتر است دقت شود اعداد با طول کمتر از k را می توان با قرار دادن صفر در سمت راست انها به اعداد ی به طول k تبدیل شوند. به طور خلاصه روش کار این الگوریتم به این صورت است که عناصر را در k مرحله با استفاده از مرتب سازی شمارشی مرتب می کند. به این صورت که ابتدا عناصر را بر حسب کم ارزش ترین رقم انها مرتب می کند و سپس بر حسب رقم بعدی کم ارزش آنها و این کار را تا رقم k ادامه داده و در انتها عناصر مرتب شده هستند. ذکر این نکته ضروریست که الگوریتم شمارشی که برای این الگوریتم استفاده می شود حتماً باید پایدار باشد. این الگوریتم به سال 1887 بر می گردد. در ان دوران از این الگوریتم در ماشین های Tabulating و همچنین ماشین های مکانیکی استفاده می شده. برای تشریح کامل این الگوریتم به صفحهٔ مرتب سازی پایه ای مراجعه کنید.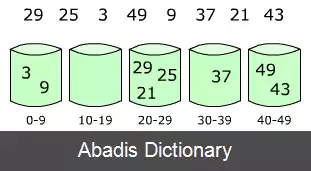
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفانواع مرتب سازی های خطی عبارتند از مرتب سازی شمارشی، مرتب سازی سطلی، مرتب سازی مبنایی و BeadSort و BrustSort و PigeonholeSort و. . .
در این الگوریتم محدودیت اعمال شده روی داده این است که کلید تمامی عناصر باید اعداد صحیح بوده و بین 1 تا m قرار بگیرند که m یک عدد ثابت است و این الگوریتم با استفاده از آرایه ای از اعداده صحیح به طول m عناصر مورد نظر را مرتب می کند. به طور خلاصه الگوریتم به این صورت عمل می کند که تعداد دفعات ظاهر شدن هر عنصر در ورودی را با کمک آرایه گرفته شده حساب می کند و سپس با این اطلاعات از ابتدا شروع کرده و هر عنصر را به تعداد دفعات ظهورش در ورودی در خروجی قرار می دهد، و با توجه به اینکه این عمل را از 1 تا m انجام می دهد خروجی مرتب شده است. برای تشریح کامل الگوریتم به صفحه مرتب سازی شمارشی مراجعه کنید.
این الگوریتم مرتب سازی برای مرتب کردن اعدادی با طول ثابت به اندازهٔ k مورد استفاده قرار می گیرد و کاربرد دارد. البته بهتر است دقت شود اعداد با طول کمتر از k را می توان با قرار دادن صفر در سمت راست انها به اعداد ی به طول k تبدیل شوند. به طور خلاصه روش کار این الگوریتم به این صورت است که عناصر را در k مرحله با استفاده از مرتب سازی شمارشی مرتب می کند. به این صورت که ابتدا عناصر را بر حسب کم ارزش ترین رقم انها مرتب می کند و سپس بر حسب رقم بعدی کم ارزش آنها و این کار را تا رقم k ادامه داده و در انتها عناصر مرتب شده هستند. ذکر این نکته ضروریست که الگوریتم شمارشی که برای این الگوریتم استفاده می شود حتماً باید پایدار باشد. این الگوریتم به سال 1887 بر می گردد. در ان دوران از این الگوریتم در ماشین های Tabulating و همچنین ماشین های مکانیکی استفاده می شده. برای تشریح کامل این الگوریتم به صفحهٔ مرتب سازی پایه ای مراجعه کنید.


wiki: مرتب سازی های خطی
