مرتب سازی مهره ای یک الگوریتم مرتب سازی طبیعی است که در سال ۲۰۰۲ توسط جاشوا جی. آرولاناندهام، کریستیان سورین کالود و مایکل جان دینین توسعه یافته است و در بولتن انجمن اروپایی برای علم کامپیوتر نظری منتشر شده است. هر دو پیاده سازی سخت افزارهای دیجیتال و آنالوگ مرتب سازی مهره ای دارای پیچیدگی زمانی ( O ( n هستند. با این حال پیاده سازی این الگوریتم در نرم افزار به میزان قابل توجهی کندتر است و تنها می تواند برای مرتب کردن لیستی از اعداد صحیح مثبت مورد استفاده قرار گیرد. همچنین به نظر می رسد که حتی در بهتربن حالت این الگوریتم به ( O ( n۲ فضا نیاز دارد.
عملیات مرتب سازی مهره ای را می توان به مهره هایی که در یک راستا به موازات یکدیگر ( در یک قطب ) قرار گرفته اند تشبیه کرد. دقیقاً همانند چرتکه. با این حال تعداد مشخصی از مهره ها در هر یک ار این قطب ها قرار می گیرند. در ابتدا معلق بودن مهره ها در قطب عمودی ممکن است مفید باشد. در اولین مرحله ترتیب نمایش بدین صورت است که مهره ها در n=5 سطر و m=4 قطب عمودی قرار می گیرند. اعداد سمت راست هر سطر تعداد مهره های موجود در آن سطر را نشان می دهد. شماره سطر اول و دوم به دلیل وحود ۳ مهره عدد صحیح و مثبت ۳، و شماره سطر بالا به دلیل. جود ۲ مهره عدد صحیح و مثبت ۲ را نشان می دهد. اگر ما بخواهیم که مهره ها سقوط کنند، سطرها اعداد صحیح ( تعداد مهره های سطر جدید ) را در مرتب سازی شرکت می دهد. سطر اول حاوی بیشترین تعداد مهره در این مجموعه و سطرn ام حاوی کمترین تعداد مهره خواهد بود. اگر در سطرهای ذکر شده یک سری از مهره ها در ستون ۱ تا k باشند، ستون های k+1 تا m پشت سر هم خالی خواهند شد و این امر برای سطرها بعدی نیز ادامه پیدا خواهد کرد. در عملیات سقوط مهره ها، در مثال فیزیکی، در واقع ما به مقادیر بزرگتر در ردیف های بالا اجازه داده ایم تا به ردیف های پایین تر انتشار یابند. اگر مقدار نشان داده شده در سطر a کوچکتر از مقدار مندرج در سطر a+1 باشد نشان گر این است که برخی از مهره های سطر a+1 در سطر a سقوط کرده اند. این مسلم است که سطر a در آن موقعیت شامل مهره ای برای جلوگیری از سقوط مهره ها از سطر a+1 نمی شود. اساس مکانیزم مرتب سازی مهره ای با اساس مرتب سازی شمارشی مشابه است. تعداد مهره ها در هر ستون مربوط به تعدادی از عناصر با ارزش برابر یا کمتر از شاخص یک ستون است.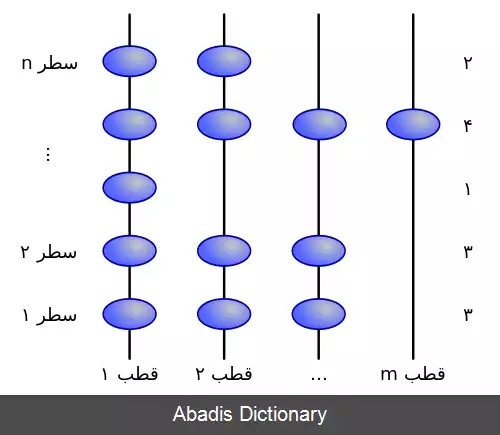
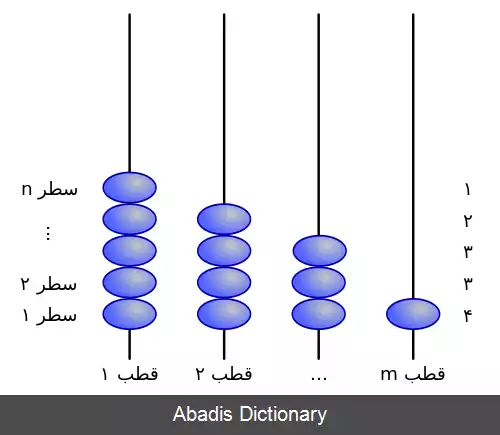

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعملیات مرتب سازی مهره ای را می توان به مهره هایی که در یک راستا به موازات یکدیگر ( در یک قطب ) قرار گرفته اند تشبیه کرد. دقیقاً همانند چرتکه. با این حال تعداد مشخصی از مهره ها در هر یک ار این قطب ها قرار می گیرند. در ابتدا معلق بودن مهره ها در قطب عمودی ممکن است مفید باشد. در اولین مرحله ترتیب نمایش بدین صورت است که مهره ها در n=5 سطر و m=4 قطب عمودی قرار می گیرند. اعداد سمت راست هر سطر تعداد مهره های موجود در آن سطر را نشان می دهد. شماره سطر اول و دوم به دلیل وحود ۳ مهره عدد صحیح و مثبت ۳، و شماره سطر بالا به دلیل. جود ۲ مهره عدد صحیح و مثبت ۲ را نشان می دهد. اگر ما بخواهیم که مهره ها سقوط کنند، سطرها اعداد صحیح ( تعداد مهره های سطر جدید ) را در مرتب سازی شرکت می دهد. سطر اول حاوی بیشترین تعداد مهره در این مجموعه و سطرn ام حاوی کمترین تعداد مهره خواهد بود. اگر در سطرهای ذکر شده یک سری از مهره ها در ستون ۱ تا k باشند، ستون های k+1 تا m پشت سر هم خالی خواهند شد و این امر برای سطرها بعدی نیز ادامه پیدا خواهد کرد. در عملیات سقوط مهره ها، در مثال فیزیکی، در واقع ما به مقادیر بزرگتر در ردیف های بالا اجازه داده ایم تا به ردیف های پایین تر انتشار یابند. اگر مقدار نشان داده شده در سطر a کوچکتر از مقدار مندرج در سطر a+1 باشد نشان گر این است که برخی از مهره های سطر a+1 در سطر a سقوط کرده اند. این مسلم است که سطر a در آن موقعیت شامل مهره ای برای جلوگیری از سقوط مهره ها از سطر a+1 نمی شود. اساس مکانیزم مرتب سازی مهره ای با اساس مرتب سازی شمارشی مشابه است. تعداد مهره ها در هر ستون مربوط به تعدادی از عناصر با ارزش برابر یا کمتر از شاخص یک ستون است.



wiki: مرتب سازی مهره ای
