مربع لاتین

مربع لاتین یک آرایهٔ مربعی ( ماتریس مربعی ) است که در هر سطر و هر ستون آن اعضای مجموعه A به طور کامل و بدون تکرار قرار داشته باشند.
مثال: در احتمالات ماتریس «متغیر تصادفی دوگانه» ( که حاصل جمع هر سطر و ستون آن یک است ) یک مربع لاتین است.
( 0 1 4 3 4 1 4 3 4 0 3 4 0 1 4 )
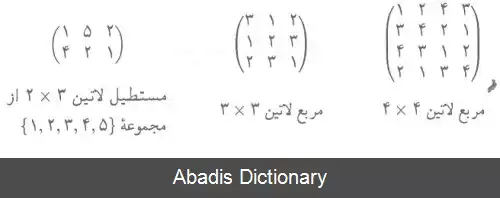
حال در مورد مستطیل ها و مربع هایی بحث می کنیم که درایه های آن اعداد صحیح و مثبت هستند. یک مستطیل لاتین A با ابعاد p×q عبارت است از  : یک ماتریس p × q که هر یک از درایه های آن عضو مجموعه {۳٬۲، 1. . . n} بوده و هیچ عضو تکراری در سطر یا ستون آن به وجود نیاید. در حالت خاص اگر p = q = n آن را مربع لاتین می نامیم. در این صورت هر سطر و هر ستون جایگشتی از مجموعه {۳٬۲، 1. . . n} است.
حال این سؤال را مطرح می کنیم که آیا یک مستطیل لاتین الزاماً بخشی از یک مربع لاتین است؟ مثال: آیا مستطیل لاتین زیر بخشی از یک مربع لاتین ۴×۴ است؟ یا به عبارت دیگر آیا می توان دو سطر دیگر به این مستطیل لاتین افزود که تبدیل به مربع لاتین ۴×۴ شود؟
( 1 2 3 4 4 3 2 1 )
به طور مشابه آیا مستطیل لاتین مقابل بخشی از مربع لاتین ۵×۵ است؟
( 1 3 4 5 3 5 1 2 5 1 3 4 )
مستطیل لاتین اول می تواند به مربع لاتین گسترش پیدا می کند. مانند:
( 1 2 3 4 4 3 2 1 2 1 4 3 3 4 1 2 )
می توان نشان داد که هر مستطیل لاتین p×q با درایه هایی از مجموعه {۳٬۲، 1. . . n} را می توان به مربع لاتین n×n گسترش داد. اما مستطیل دوم قابل گسترش نیست. چون به ستون های اول و دوم وسوم باید عدد «۲» اضافه شود. چون این سه عدد «۲» باید در دو سطر قرار گیرند پس دو تا از آن ها در یک سطر واقع شده اند؛ بنابراین مربع بدست آمده لاتین نخواهد بود. قبل از این که به بیان قضایای مورد نظر در این بحث بپردازیم، ابتدا به صورت دو قضیه و یک لم کمکی اشاره می کنیم:
۱ ) قضیه هال ( صورت ماتریسی )   : ماتریس M یک ماتریس m× n با درایه های صفر و یک است. در این صورت در هر سطر آن یک عدد ۱ وجود دارد و در هیچ ستونی بیش از یک عدد ۱ وجود ندارد اگر و تنها اگر برای هر مجموعه از سطرها ( مثلاً r تایی ) تعداد ستون هایی که ۱های این سطرها در آن ها قرار دارند، حد اقل برابر r باشد.
۲ ) یک خانواده از مجموعه ها به صورت{ S={A1، A2، A3 ، . . . ، An را در نظر می گیریم. مجموعه P را نیز یصورت زیر فرض می کنیم:
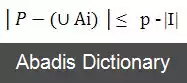
P زیر مجموعهٔ A1∪A2∪. . . ∪An