مدل های زیادی مبتنی بر زنجیرهٔ مارکوف، برای مدل سازی سیر فرگشتی دی ان ای ارائه شده است. معمولاً مدل های جانشینی ارایه شده با هم در پارامترهایی که برای توضیح نرخ جانشینی یک نوکلئوتید در طول فرگشت دی ان ای در نظر گرفته می شوند، متفاوت هستند. این مدل ها معمولاً در آنالیز فیلوژنتیک مولکولی استفاده می شوند. به طور خاص از مدل های ارائه شده در برآورد درست نمایی بیشینهی درخت و تخمین فاصلهٔ فرگشتی میان توالی ها با داشتن فواصل مشاهده شده در میان آن ها، استفاده می شود. روش های مبتنی بر درست نمایی بیشینه به مدل وابسته هستند به طوری که اگر بخشی از اطلاعات موجود در داده ها را در نظر نگیرد، نتایج این روش بسیار ضعیف خواهد بود. مدل های مبتنی بر مارکوف در تحلیل داده ها تنها جانشینی در یک توالی را در نظر گرفته و حذف و اضافه شدن در توالی را نادیده می گیرند. [ ۱]
رویکردهای مختلفی برای ساخت درخت فیلوژنی و تخمین فاصلهٔ زمانی میان موجودات وجود دارد. روش ها را می توان به ۳ دستهٔ زیر تقسیم کرد:
• روش های مبتنی بر فاصله مانند روش UPGMA و اتصال هم سایگی
• روش های مبتنی بر بیشینه صرفه جویی
• روش های مبتنی بر درست نمایی بیشینه
یکی از مدل های پرکابرد برای استفاده از درست نمایی بیشینه استفاده از مدل مارکوف در تغییر جایگاه های توالی در طول زمان است. [ ۲] مدل های فرگشتی دی ان ای توضیح دهندهٔ وضعیت فرگشتی دی ان ای به عنوان رشته ای شامل ۴ حرف هستند. مدل های مارکوف به طور دقیق نحوهٔ ایجاد جهش یا عمل انتخاب طبیعی را توضیح نمی دهند، بلکه نرخ نسبتی جهش ها را در رشتهٔ دی ان ای مدل می کنند. به طور مثال در تغییرات توالی ها، نابرابری احتمال جهش ها و احتمال از بین رفتن اللهای ناسازگار با محیط، مسئول نرخ بالای جایگزینی انتقالی نسبت به تراگشت در رشته های در حال تغییر هستند. در حالی که در مدل Kimura80 که در ادامه توضیح داده شده است، تأثیر احتمال نابرابر جهش ها و احتمال از بین رفتن الل های ناسازگار با محیط تنها در پارامتری در نظر گرفته شده است که نرخ نسبی جایگزینی انتقالی را به تراگشت مدل می کند.
تحلیل های فرگشتی توالی ها برای مقیاس های زمانی مختلفی انجام شده است، از این رو بیان مدل ها به کمک نرخ لحظه ای تغییر وضعیت جایگاه های توالی قابل قبول است. ماتریس Q که در ادامه آورده شده است، نشان دهندهٔ این نرخ تغییر در میان وضعیت های تعریف شده در مسئله است. در صورتی که بدانیم که وضعیت شروع در یک جایگاه از توالی کدام است ( وضعیت هر جایگاه برای یک توالی از دی ان ای نوع نوکلئوتید موجود در آن جایگاه است ) ، آن گاه می توان به کمک ماتریس Q در مدل و فاصلهٔ زمانی میان جد و فرزند، احتمال تعداد تغییرها و احتمال رسیدن به هر کدام از وضعیت های تعریف شده را استخراج کرد. جزییات مربوط به رسیدن از ماتریس نرخ به ماتریس احتمال در مدل های ریاضیاتی جانشینی توضیح داده می شود. در نظر گرفتن نرخ آنی در مدل، باعث بی نیازی آن از محاسبهٔ پارامترهای سطوح درخت فیلوژنی به صورت جداگانه برای هر سطح می شود، زیرا احتمال رسیدن از حالت ابتدایی به حالت انتهایی به صورت مستقیم محاسبه می گردد.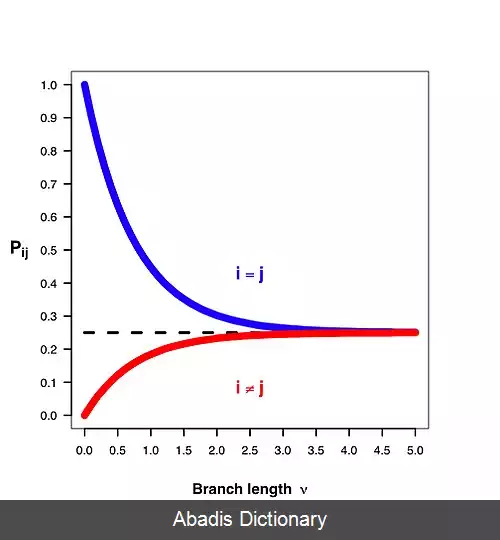
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفرویکردهای مختلفی برای ساخت درخت فیلوژنی و تخمین فاصلهٔ زمانی میان موجودات وجود دارد. روش ها را می توان به ۳ دستهٔ زیر تقسیم کرد:
• روش های مبتنی بر فاصله مانند روش UPGMA و اتصال هم سایگی
• روش های مبتنی بر بیشینه صرفه جویی
• روش های مبتنی بر درست نمایی بیشینه
یکی از مدل های پرکابرد برای استفاده از درست نمایی بیشینه استفاده از مدل مارکوف در تغییر جایگاه های توالی در طول زمان است. [ ۲] مدل های فرگشتی دی ان ای توضیح دهندهٔ وضعیت فرگشتی دی ان ای به عنوان رشته ای شامل ۴ حرف هستند. مدل های مارکوف به طور دقیق نحوهٔ ایجاد جهش یا عمل انتخاب طبیعی را توضیح نمی دهند، بلکه نرخ نسبتی جهش ها را در رشتهٔ دی ان ای مدل می کنند. به طور مثال در تغییرات توالی ها، نابرابری احتمال جهش ها و احتمال از بین رفتن اللهای ناسازگار با محیط، مسئول نرخ بالای جایگزینی انتقالی نسبت به تراگشت در رشته های در حال تغییر هستند. در حالی که در مدل Kimura80 که در ادامه توضیح داده شده است، تأثیر احتمال نابرابر جهش ها و احتمال از بین رفتن الل های ناسازگار با محیط تنها در پارامتری در نظر گرفته شده است که نرخ نسبی جایگزینی انتقالی را به تراگشت مدل می کند.
تحلیل های فرگشتی توالی ها برای مقیاس های زمانی مختلفی انجام شده است، از این رو بیان مدل ها به کمک نرخ لحظه ای تغییر وضعیت جایگاه های توالی قابل قبول است. ماتریس Q که در ادامه آورده شده است، نشان دهندهٔ این نرخ تغییر در میان وضعیت های تعریف شده در مسئله است. در صورتی که بدانیم که وضعیت شروع در یک جایگاه از توالی کدام است ( وضعیت هر جایگاه برای یک توالی از دی ان ای نوع نوکلئوتید موجود در آن جایگاه است ) ، آن گاه می توان به کمک ماتریس Q در مدل و فاصلهٔ زمانی میان جد و فرزند، احتمال تعداد تغییرها و احتمال رسیدن به هر کدام از وضعیت های تعریف شده را استخراج کرد. جزییات مربوط به رسیدن از ماتریس نرخ به ماتریس احتمال در مدل های ریاضیاتی جانشینی توضیح داده می شود. در نظر گرفتن نرخ آنی در مدل، باعث بی نیازی آن از محاسبهٔ پارامترهای سطوح درخت فیلوژنی به صورت جداگانه برای هر سطح می شود، زیرا احتمال رسیدن از حالت ابتدایی به حالت انتهایی به صورت مستقیم محاسبه می گردد.

