در هندسه، دستگاه مختصات خمیده خطی ( به انگلیسی: Curvilinear Coordinates ) ، یک دستگاه مختصات در فضای اقلیدسی است که در آن، خطوط مختصات می توانند خمیده باشند. دستگاه های مختصات دکارتی، استوانه ای و کروی، نمونه هایی خاص از دستگاه مختصات خمیده خط هستند.
مختصات، اغلب برای تعریف مکان یا توزیع کمیت های فیزیکی که ممکن است نرده ای، برداری یا تانسوری باشند، به کار می رود. بسته به کاربرد، ممکن است یک دستگاه مختصات خمیده خط ساده تر از مختصات دکارتی باشد. برای مثال، یک مسئلهٔ فیزیکی با تقارن کروی در فضای R3 ( مانند حرکت یک ذره در یک میدان ) ، در دستگاه مختصات کروی، آسان تر از دستگاه دکارتی حل می شود. دستگاه مختصات کروی، یکی از پرکاربردترین دستگاه های مختصات خمیده خط در مباحثی مانند علوم زمین، نقشه نگاری، مهندسی و فیزیک ( به ویژه مکانیک کوانتوم و نسبیت ) به شمار می رود.
دستگاه مختصات خمیده خط، توصیفی کلی و یکپارچه از دستگاه های مختصات استاندارد ارائه می دهد. اصطلاحات عمومی حساب برداری و تانسورها مانند گرادیان، دیورژانس، کرل و عملگر لاپلاس برای مختصات خمیده خط هم معتبرند.
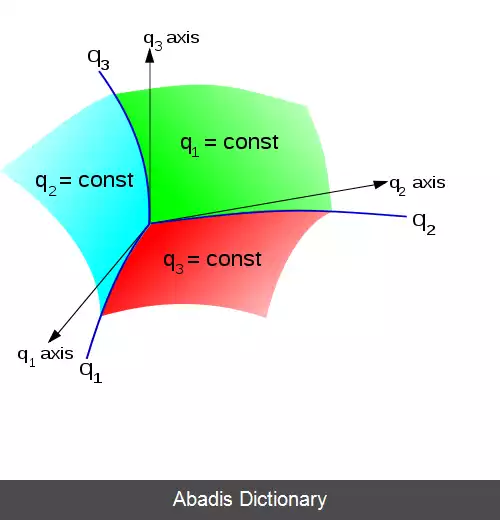
هر نقطه دلخواه p در فضای سه بعدی با استفاده از مختصات دکارتی به صورت یک سه تایی ( x، y، z ) نشان داده می شود. سطوح ثابت=x، ثابت=y و ثابت=z مسطح و عمود بر یکدیگرند؛ بنابراین از فصل مشترک این سه صفحه عمود برهم محورهای راست خط این دستگاه مختصات بدست می آیند. اکنون فرض کنید سه دسته سطح ثابت=q۱، ثابت=q۲ و ثابت=q۳ داشته باشید که این بار الزاماً عمود برهم یا مسطح نباشند، یعنی این سه دسته سطح می توانند خمیده شکل بوده و عمود برهم نباشند. چون فصل مشترک سه دسته سطح q۱ و q۲ و q۳ با یکدیگر به صورت خط های خمیده شکل اند، مختصات ( q۱، q۲، q۳ ) را مختصات خمیده خط می نامند.
ارتباط بین مختصات خمیده خط و دکارتی، با استفاده از تبدیل های وارون پذیر زیر برقرار می شود:
هر نقطه می تواند به صورت یک بردار مکان r در هر دستگاه مختصات نشان داده شود. برای دستگاه مختصات دکارتی:
که x, y, z مختصه های بردار مکان نسبت به بردارهای پایه ex, ey, ez هستند. بردارهای پایه مختصات دکارتی، پایه استاندارد بردارها هستند.
برای مختصات خمیده خط، بردار مکان r به صورت زیر نوشته می شود:
که h1, h2, h3 ضرایب مقیاس بوده و نشان دهندهٔ تغییر شکل ایجادشده از مختصات دکارتی به مختصات خمیده خط هستند و h1q1, h2q2, h3q3 مختصه های بردار مکان و b1, b2, b3 بردارهای پایه مختصات خمیده خط هستند.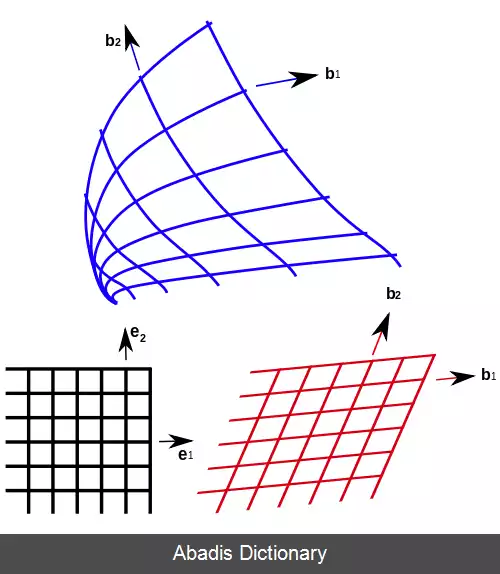
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمختصات، اغلب برای تعریف مکان یا توزیع کمیت های فیزیکی که ممکن است نرده ای، برداری یا تانسوری باشند، به کار می رود. بسته به کاربرد، ممکن است یک دستگاه مختصات خمیده خط ساده تر از مختصات دکارتی باشد. برای مثال، یک مسئلهٔ فیزیکی با تقارن کروی در فضای R3 ( مانند حرکت یک ذره در یک میدان ) ، در دستگاه مختصات کروی، آسان تر از دستگاه دکارتی حل می شود. دستگاه مختصات کروی، یکی از پرکاربردترین دستگاه های مختصات خمیده خط در مباحثی مانند علوم زمین، نقشه نگاری، مهندسی و فیزیک ( به ویژه مکانیک کوانتوم و نسبیت ) به شمار می رود.
دستگاه مختصات خمیده خط، توصیفی کلی و یکپارچه از دستگاه های مختصات استاندارد ارائه می دهد. اصطلاحات عمومی حساب برداری و تانسورها مانند گرادیان، دیورژانس، کرل و عملگر لاپلاس برای مختصات خمیده خط هم معتبرند.
هر نقطه دلخواه p در فضای سه بعدی با استفاده از مختصات دکارتی به صورت یک سه تایی ( x، y، z ) نشان داده می شود. سطوح ثابت=x، ثابت=y و ثابت=z مسطح و عمود بر یکدیگرند؛ بنابراین از فصل مشترک این سه صفحه عمود برهم محورهای راست خط این دستگاه مختصات بدست می آیند. اکنون فرض کنید سه دسته سطح ثابت=q۱، ثابت=q۲ و ثابت=q۳ داشته باشید که این بار الزاماً عمود برهم یا مسطح نباشند، یعنی این سه دسته سطح می توانند خمیده شکل بوده و عمود برهم نباشند. چون فصل مشترک سه دسته سطح q۱ و q۲ و q۳ با یکدیگر به صورت خط های خمیده شکل اند، مختصات ( q۱، q۲، q۳ ) را مختصات خمیده خط می نامند.
ارتباط بین مختصات خمیده خط و دکارتی، با استفاده از تبدیل های وارون پذیر زیر برقرار می شود:
هر نقطه می تواند به صورت یک بردار مکان r در هر دستگاه مختصات نشان داده شود. برای دستگاه مختصات دکارتی:
که x, y, z مختصه های بردار مکان نسبت به بردارهای پایه ex, ey, ez هستند. بردارهای پایه مختصات دکارتی، پایه استاندارد بردارها هستند.
برای مختصات خمیده خط، بردار مکان r به صورت زیر نوشته می شود:
که h1, h2, h3 ضرایب مقیاس بوده و نشان دهندهٔ تغییر شکل ایجادشده از مختصات دکارتی به مختصات خمیده خط هستند و h1q1, h2q2, h3q3 مختصه های بردار مکان و b1, b2, b3 بردارهای پایه مختصات خمیده خط هستند.


wiki: مختصات خمیده خطی
