در ریاضیات، یک مجموعه تراز ( به انگلیسی: level set ) برای یک تابع حقیقی - مقدار f با n تا متغیر حقیقی، مجموعه ای است که تابع در آن، یک مقدار ثابت معین c را به خود می گیرد، یعنی:
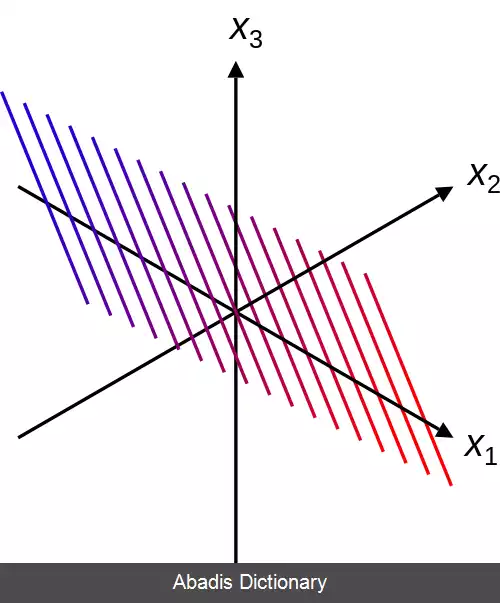
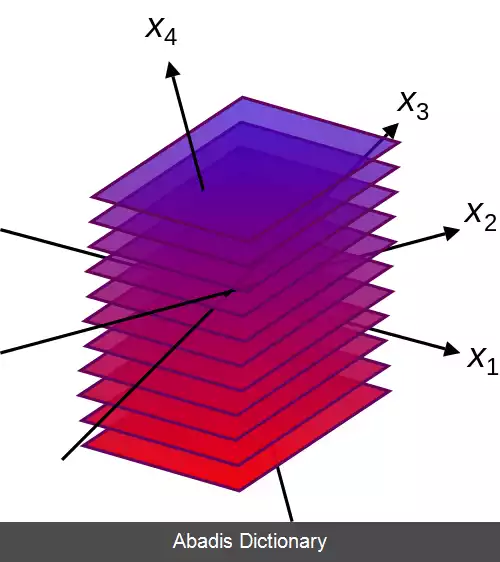
وقتیکه تعداد متغیرهای مستقل برابر دو است، به مجموعه تراز، منحنی تراز می گویند که خط تراز ( مرز ) [ ۱] ( به انگلیسی: contour line ) یا خط همبار ( به انگلیسی: isoline ) هم نام دارد؛ از این رو یک منحنی تراز برابر مجموعه همه راه حل های حقیقی - مقدار از یک معادله با دو متغیر x1 و x2 است. وقتیکه n = ۳ است، به مجموعه تراز یک رویه تراز ( به انگلیسی: level surface ) ( یا هم رویه ( به انگلیسی: isosurface ) ) می گویند؛ از این رو یک رویه تراز برابر مجموعه همه ریشه های حقیقی - مقدار از یک معادله با سه متغیر x1، x2 و x3 است. برای مقادیر بالاتر از n، مجموعه تراز یک اَبَررویه تراز است، یعنی مجموعه همه ریشه های حقیقی - مقدار از یک معادله با n > 3 متغیر.
یک مجموعه تراز حالت خاصی از یک تار است.
مجموعه های تراز در بسیاری از کاربردها دیده شده اند که اکثراً در آن ها نام متفاوتی دارند.
برای مثال، یک منحنی ضمنی یک منحنی تراز است، که به صورت مستقل از منحنی های همسایه اش درنظر گرفته می شود، و روی این موضوع تأکید دارد که چنین منحنی ای توسط یک معادله ضمنی تعریف شده است. به صورت مشابه، یک رویه تراز را گاهی رویه ضمنی یا یک هم رویه می نامند.
نام هم مرز ( به انگلیسی: isocontour ) هم به کار می رود، که به معنی یک مرز با ارتفاع برابر است. در زمینه های کاربردی مختلف، به هم مرز نام های خاصی داده شده است، که معمولاً نشان دهنده طبیعت مقادیر تابع مورد نظر است، مثل همفشار، همدما، همزمان، هم رنگ، متساوی التولید، و منحنی بی تفاوتی است.
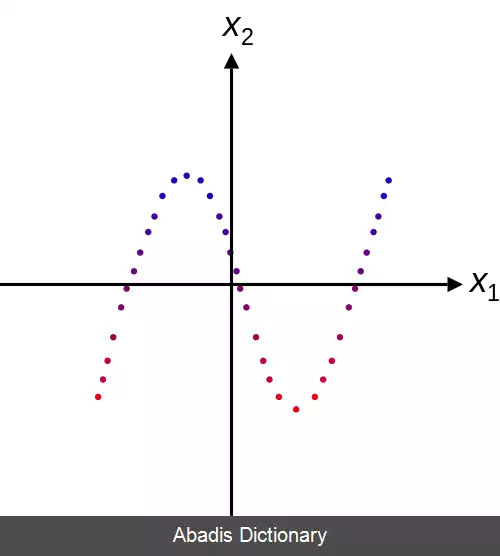
فاصله اقلیدسی دو - بعدی را در نظر بگیرید d ( x , y ) = x 2 + y 2 یک مجموعه تراز L r ( d ) از این تابع شامل آن نقاطی است که در فاصله r از مبدأ قرار می گیرند، که یک دایره تشکیل می دهند. برای مثال ( 3 , 4 ) ∈ L 5 ( d ) ، زیرا d ( 3 , 4 ) = 5 است. به صورت هندسی، این یعنی نقطه ( 3 , 4 ) روی دایره با شعاع ۵ با مرکز مبدأ می افتد. به صورت کلی تر، یک کره در یک فضای متری ( M , m ) با شعاع r و مرکز x ∈ M را می توان به صورت مجموعه تراز L r ( y ↦ m ( x , y ) ) تعریف کرد. مثال دوم نمودار تابع هیملبلو است که در شکل زیر نمایش داده شده است. هر منحنی نشان داده شده یک منحنی تراز از تابع است، که به صورت لگاریتمی فاصله دهی شده اند: اگر یک منحنی نمایش دهنده L x باشد، آنوقت این منحنی به صورت مستقیم «درونی» نمایش دهنده L x / 10 است، و به صورت مستقیم «بیرونی» نمایش دهنده L 10 x است.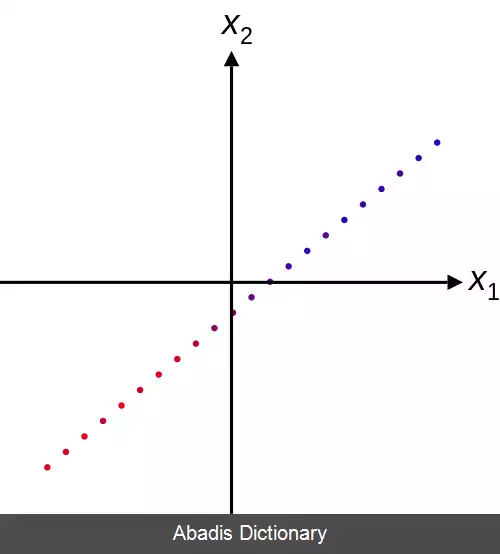
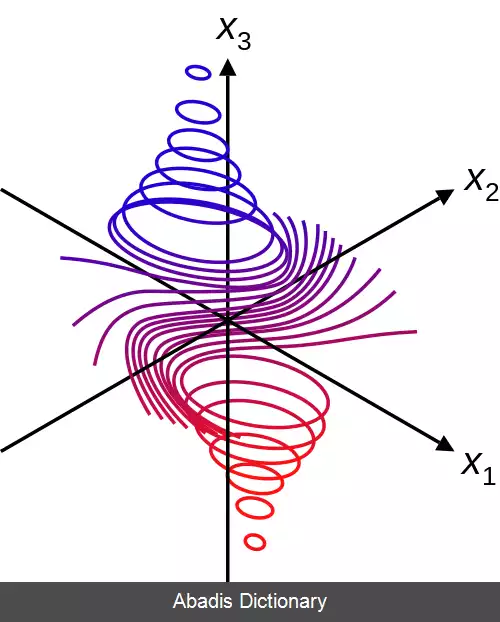
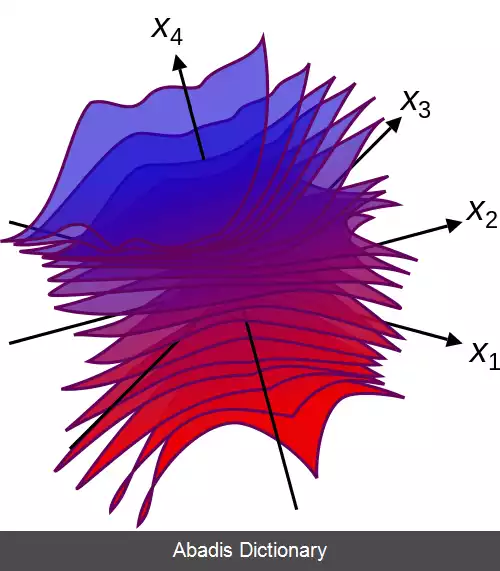
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفوقتیکه تعداد متغیرهای مستقل برابر دو است، به مجموعه تراز، منحنی تراز می گویند که خط تراز ( مرز ) [ ۱] ( به انگلیسی: contour line ) یا خط همبار ( به انگلیسی: isoline ) هم نام دارد؛ از این رو یک منحنی تراز برابر مجموعه همه راه حل های حقیقی - مقدار از یک معادله با دو متغیر x1 و x2 است. وقتیکه n = ۳ است، به مجموعه تراز یک رویه تراز ( به انگلیسی: level surface ) ( یا هم رویه ( به انگلیسی: isosurface ) ) می گویند؛ از این رو یک رویه تراز برابر مجموعه همه ریشه های حقیقی - مقدار از یک معادله با سه متغیر x1، x2 و x3 است. برای مقادیر بالاتر از n، مجموعه تراز یک اَبَررویه تراز است، یعنی مجموعه همه ریشه های حقیقی - مقدار از یک معادله با n > 3 متغیر.
یک مجموعه تراز حالت خاصی از یک تار است.
مجموعه های تراز در بسیاری از کاربردها دیده شده اند که اکثراً در آن ها نام متفاوتی دارند.
برای مثال، یک منحنی ضمنی یک منحنی تراز است، که به صورت مستقل از منحنی های همسایه اش درنظر گرفته می شود، و روی این موضوع تأکید دارد که چنین منحنی ای توسط یک معادله ضمنی تعریف شده است. به صورت مشابه، یک رویه تراز را گاهی رویه ضمنی یا یک هم رویه می نامند.
نام هم مرز ( به انگلیسی: isocontour ) هم به کار می رود، که به معنی یک مرز با ارتفاع برابر است. در زمینه های کاربردی مختلف، به هم مرز نام های خاصی داده شده است، که معمولاً نشان دهنده طبیعت مقادیر تابع مورد نظر است، مثل همفشار، همدما، همزمان، هم رنگ، متساوی التولید، و منحنی بی تفاوتی است.
فاصله اقلیدسی دو - بعدی را در نظر بگیرید d ( x , y ) = x 2 + y 2 یک مجموعه تراز L r ( d ) از این تابع شامل آن نقاطی است که در فاصله r از مبدأ قرار می گیرند، که یک دایره تشکیل می دهند. برای مثال ( 3 , 4 ) ∈ L 5 ( d ) ، زیرا d ( 3 , 4 ) = 5 است. به صورت هندسی، این یعنی نقطه ( 3 , 4 ) روی دایره با شعاع ۵ با مرکز مبدأ می افتد. به صورت کلی تر، یک کره در یک فضای متری ( M , m ) با شعاع r و مرکز x ∈ M را می توان به صورت مجموعه تراز L r ( y ↦ m ( x , y ) ) تعریف کرد. مثال دوم نمودار تابع هیملبلو است که در شکل زیر نمایش داده شده است. هر منحنی نشان داده شده یک منحنی تراز از تابع است، که به صورت لگاریتمی فاصله دهی شده اند: اگر یک منحنی نمایش دهنده L x باشد، آنوقت این منحنی به صورت مستقیم «درونی» نمایش دهنده L x / 10 است، و به صورت مستقیم «بیرونی» نمایش دهنده L 10 x است.






wiki: مجموعه تراز
