مثلث سرعتها مثلثی فرضی در مطالعه و بررسی توربوماشینها در مکانیک سیالات است که اضلاع سازنده آن در هر نقطه از سیال عبوری از توربوماشین، از سه بردار سرعت محیطی چرخ توربوماشین، بردار سرعت نسبی بین ذره سیال و چرخ توربوماشین و بردار سرعت مطلق ذره سیال در نقطه مورد بررسی تشکیل شده است. با استفاده از مثلث سرعتها می توان معادلات اصلی مکانیک سیالات مانند معادله پیوستگی سیال، معادله مقدار حرکت خطی و لنگر زاویه ای سیال و همینطور قوانین ترمودینامیکی مانند قانون قانون اول و دوم ترمودینامیک را در عبور سیال از چرخ توربوماشین در حین تبادل انرژی و قدرت بین سیال و چرخ بر اساس مؤلفه های سرعت سیال و سرعت محیطی چرخ در ورودی و خروجی چرخ توربوماشین، بیان نمود. [ ۱]
المانی از سیال را در لحظه t و در نقطه p به فاصله R از محور دوران و داخل چرخ توربوماشین در نظر بگیرید. سرعت این المان در دستگاه نسبی متصل به چرخ، W → و امتداد آن مماس بر خط جریان مربوطه میباشد. در این لحظه، چرخ با سرعت زاویه ای ω دوران نموده و نقطه p از آن دارای سرعت محیطی U → خواهد بود به طوریکه | U → | = R . ω . بنابراین سرعت مطلق المان سیال C → ، از جمع بردارهای سرعت محیطی U → و سرعت نسبی W → به دست می آید[ ۱] [ ۲] :
C → = U → + W →
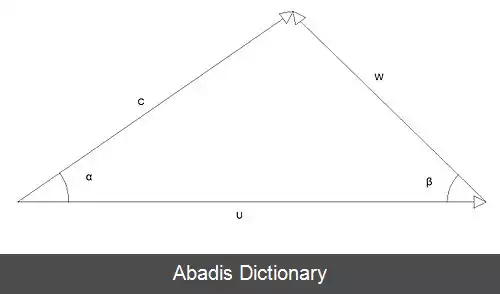
سه بردار U → و W → و C → تشکیل مثلثی میدهند که آن را مثلث سرعتها در نقطه p و در لحظه t مینامند. اگر جریان در چرخ دائمی باشد، مثلث سرعتها در نقطه p بستگی به زمان ندارد و ثابت خواهد بود. به طور قراردادی، زاویه بین بردارهای U → و C → را با α و زاویه بین W → و جهت مخالف U → را با β نشان میدهند. در رسم مثلث سرعتها سرعت محیطی چرخ توربوماشین، U → ، به عنوان قاعده مثلث انتخاب میشود[ ۲] [ ۱] .
در روابط معمولاً تصاویر سرعتهای مطلق ونسبی در امتداد سرعت محیطی و امتداد عمود بر آن مورد استفاده قرار می گیرند. مؤلفه سرعتها در امتداد U با اندیس u و مؤلفه های عمود بر U در حالت کلی با اندیس m نشان داده می شوند:
C u = C cos α
W u = W cos β
C m = C sin α
W m = W sin β
مؤلفه های C m و W m که ارتفاع مثلث سرعتهاست، عمود بر سطح جریان بوده و با دبی حجمی جریان سیال عبوری متناسب است[ ۱] . مؤلفه نصف النهاری سرعت، C m ، در توربوماشینهای شعاعی با اندیس r و در توربوماشینهای محوری با اندیس a نشان داده میشود.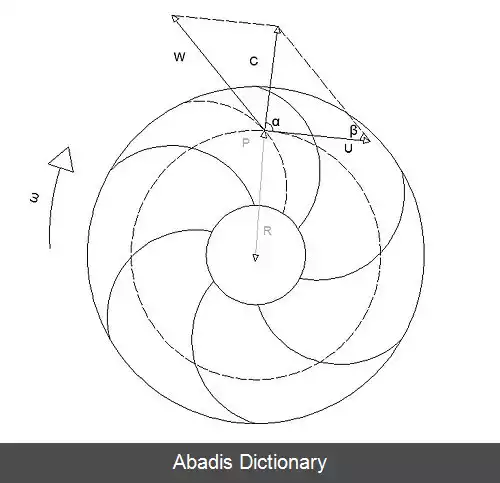
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالمانی از سیال را در لحظه t و در نقطه p به فاصله R از محور دوران و داخل چرخ توربوماشین در نظر بگیرید. سرعت این المان در دستگاه نسبی متصل به چرخ، W → و امتداد آن مماس بر خط جریان مربوطه میباشد. در این لحظه، چرخ با سرعت زاویه ای ω دوران نموده و نقطه p از آن دارای سرعت محیطی U → خواهد بود به طوریکه | U → | = R . ω . بنابراین سرعت مطلق المان سیال C → ، از جمع بردارهای سرعت محیطی U → و سرعت نسبی W → به دست می آید[ ۱] [ ۲] :
C → = U → + W →
سه بردار U → و W → و C → تشکیل مثلثی میدهند که آن را مثلث سرعتها در نقطه p و در لحظه t مینامند. اگر جریان در چرخ دائمی باشد، مثلث سرعتها در نقطه p بستگی به زمان ندارد و ثابت خواهد بود. به طور قراردادی، زاویه بین بردارهای U → و C → را با α و زاویه بین W → و جهت مخالف U → را با β نشان میدهند. در رسم مثلث سرعتها سرعت محیطی چرخ توربوماشین، U → ، به عنوان قاعده مثلث انتخاب میشود[ ۲] [ ۱] .
در روابط معمولاً تصاویر سرعتهای مطلق ونسبی در امتداد سرعت محیطی و امتداد عمود بر آن مورد استفاده قرار می گیرند. مؤلفه سرعتها در امتداد U با اندیس u و مؤلفه های عمود بر U در حالت کلی با اندیس m نشان داده می شوند:
C u = C cos α
W u = W cos β
C m = C sin α
W m = W sin β
مؤلفه های C m و W m که ارتفاع مثلث سرعتهاست، عمود بر سطح جریان بوده و با دبی حجمی جریان سیال عبوری متناسب است[ ۱] . مؤلفه نصف النهاری سرعت، C m ، در توربوماشینهای شعاعی با اندیس r و در توربوماشینهای محوری با اندیس a نشان داده میشود.


wiki: مثلث سرعت
