متغیر تصادفی
فرهنگستان زبان و ادب
دانشنامه عمومی
در آمار و احتمال، متغیر تصادفی متغیری است که مقدار آن از اندازه گیری برخی از انواع فرایندهای کاتوره ای بدست می آید. به طور رسمی تر، ورتنده کاتوره ای تابعی است از فضای نمونه به اعداد حقیقی. به طور مستقیم ورتنده کاتوره ای توصیف عددی خروجی یک آزمایش است ( مثل برآمدهای ممکن از پرتاب دو تاس ( ۱و۱ ) و ( ۱و۲ ) و غیره ) .
ورتنده های کاتوره ای به دو نوع گسسته ( ورتنده کاتوره ای که ممکن است تعداد محدود یا توالی نامحدودی از مقادیر را بگیرد ) و پیوسته ( متغیری که ممکن است هر مقدار عددی در یک یا چند بازه را بگیرد ) طبقه بندی می شوند. مقادیر ممکن یک ورتنده کاتوره ای می تواند نشان دهندهٔ برآمدهای آزمایشی که هنوز انجام نشده یا مقادیر بالقوهٔ یک کمیت که مقدارهای موجود آن نامطمئن هستند ( مثلاً در نتیجه اطلاعات ناقص یا اندازه گیری نادقیق ) باشد. یک ورتنده کاتوره ای می تواند به عنوان یک کمیت که مقدارش ثابت نیست و مقادیر مختلفی را می تواند بگیرد در نظر گرفته شود و توزیع احتمال برای توصیف احتمال اتفاق افتادن آن مقادیر استفاده می شود.
متغیرهای کاتوره ای معمولاً با اعداد حقیقی مقداردهی می شوند؛ ولی می توان انواع دلخواهی مانند مقدارهای بولی، اعداد مختلط، بردارها، ماتریس ها، دنباله ها، درخت ها، مجموعه ها، شکل ها، منیفلدها، توابع و فرایندها را در نظر گرفت. عبارت المان کاتوره ای همه این نوع مفاهیم را دربرمی گیرد.
متغیرهای کاتوره ای که با اعداد حقیقی مقداردهی می شوند، در علوم برای پیش بینی براساس داده های بدست آمده از آزمایش های علمی استفاده می شوند. علاوه بر کاربردهای علمی، متغیرهای کاتوره ای برای آنالیز بازی های قمار و پدیده های کاتوره ای به وجود آمدند. در چنین مواردی تابعی که خروجی را به یک عدد حقیقی می نگارد معمولاً یک تابع همانی یا به طور مشابه یک تابع بدیهی است و به طور صریح توصیف نشده است. با این وجود در بسیاری از موارد بهتر است ورتنده کاتوره ای را به صورت توابعی از سایر متغیرهای کاتوره ای در نظر بگیریم که دراینصورت تابع نگاشت استفاده شده در تعریف یک ورتنده کاتوره ای مهم می شود. به عنوان مثال، توان دو یک ورتنده کاتوره ای با توزیع استاندارد ( نرمال ) خود یک ورتنده کاتوره ای با توزیع کی دو است. شهود این مطلب بدین صورت است که تصور کنید اعداد کاتوره ای بسیاری با توزیع نرمال تولید کرده و هرکدام را به توان دو برسانیم و سپس هیستوگرام داده های بدست آمده را بکشیم در اینصورت اگر داده ها به تعداد کافی باشند، نمودار هیستوگرام تابع چگالی توزیع کی دو را با یک درجه آزادی تقریب خواهد زد.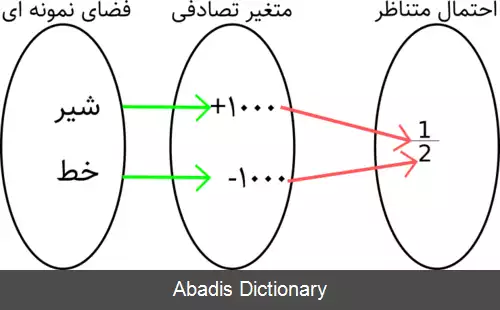
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفورتنده های کاتوره ای به دو نوع گسسته ( ورتنده کاتوره ای که ممکن است تعداد محدود یا توالی نامحدودی از مقادیر را بگیرد ) و پیوسته ( متغیری که ممکن است هر مقدار عددی در یک یا چند بازه را بگیرد ) طبقه بندی می شوند. مقادیر ممکن یک ورتنده کاتوره ای می تواند نشان دهندهٔ برآمدهای آزمایشی که هنوز انجام نشده یا مقادیر بالقوهٔ یک کمیت که مقدارهای موجود آن نامطمئن هستند ( مثلاً در نتیجه اطلاعات ناقص یا اندازه گیری نادقیق ) باشد. یک ورتنده کاتوره ای می تواند به عنوان یک کمیت که مقدارش ثابت نیست و مقادیر مختلفی را می تواند بگیرد در نظر گرفته شود و توزیع احتمال برای توصیف احتمال اتفاق افتادن آن مقادیر استفاده می شود.
متغیرهای کاتوره ای معمولاً با اعداد حقیقی مقداردهی می شوند؛ ولی می توان انواع دلخواهی مانند مقدارهای بولی، اعداد مختلط، بردارها، ماتریس ها، دنباله ها، درخت ها، مجموعه ها، شکل ها، منیفلدها، توابع و فرایندها را در نظر گرفت. عبارت المان کاتوره ای همه این نوع مفاهیم را دربرمی گیرد.
متغیرهای کاتوره ای که با اعداد حقیقی مقداردهی می شوند، در علوم برای پیش بینی براساس داده های بدست آمده از آزمایش های علمی استفاده می شوند. علاوه بر کاربردهای علمی، متغیرهای کاتوره ای برای آنالیز بازی های قمار و پدیده های کاتوره ای به وجود آمدند. در چنین مواردی تابعی که خروجی را به یک عدد حقیقی می نگارد معمولاً یک تابع همانی یا به طور مشابه یک تابع بدیهی است و به طور صریح توصیف نشده است. با این وجود در بسیاری از موارد بهتر است ورتنده کاتوره ای را به صورت توابعی از سایر متغیرهای کاتوره ای در نظر بگیریم که دراینصورت تابع نگاشت استفاده شده در تعریف یک ورتنده کاتوره ای مهم می شود. به عنوان مثال، توان دو یک ورتنده کاتوره ای با توزیع استاندارد ( نرمال ) خود یک ورتنده کاتوره ای با توزیع کی دو است. شهود این مطلب بدین صورت است که تصور کنید اعداد کاتوره ای بسیاری با توزیع نرمال تولید کرده و هرکدام را به توان دو برسانیم و سپس هیستوگرام داده های بدست آمده را بکشیم در اینصورت اگر داده ها به تعداد کافی باشند، نمودار هیستوگرام تابع چگالی توزیع کی دو را با یک درجه آزادی تقریب خواهد زد.

wiki: متغیر تصادفی
