ماشین بولتسمان ( به انگلیسی: Boltzmann Machine ) مدلی برای یادگیری خودران است. این مدل نوعی از شبکه عصبی با ارتباطات بدون جهت است. دلیل جذابیت ماشین بولتسمان، محلی بودن الگوریتم آموزش آنها و نیز رایانش موازی و همچنین شباهت پویایی آن به فرایند های فیزیکی است. [ ۱]
ماشین های بولتسمان با ارتباطات های بدون محدودیت، معمولا برای حل مسائل عملی یادگیری ماشین مناسب نیستند، اما با محدود کردن صحیح ارتباطات در ماشین بولتسمان، می توان آن را برای حل مسئله های دنیای واقعی بهینه کرد. این ماشین به نام توزیع بولتسمان در مکانیک آماری نام گذاری شده است که در تابع نمونه گیری آنها استفاده می شود. نوع عمومی تر این مدل در یادگیری ماشین، مدل های مبتنی بر انرژی هستند. [ ۲]
ماشین بولتسمان، شبکه ای از واحد های دودویی است که یک مقدار "انرژی" دارد. وزن های ماشین بولتسمان تصادفی اند و مقدار انرژی ماشین از رابطه ی زیر به دست می آید:
E = − ( ∑ i < j w i j s i s j + ∑ i θ i s i )
که:
• w i j {\displaystyle w_{ij}} وزن ارتباط بین واحد های i {\displaystyle i} و j {\displaystyle j} است.
• s i {\displaystyle s_{i}} وضعیت واحد i {\displaystyle i} است. s i ∈ { 0 , 1 } {\displaystyle s_{i}\in \{0, 1\}}
• θ i {\displaystyle \theta _{i}} مقدار اریبی واحد i {\displaystyle i} است.
وزن ها را می توان به صورت یک ماتریس W = نشان داد که درایه های روی قطر اصلی آن صفر هستند.
تفاوت مقدار انرژی ماشین در دو حالت خاموش و روشن بودن یک واحد مشخص، که به صورت Δ E i نوشته می شود از رابطه ی زیر به دست آید:
Δ E i = ∑ i ≠ j w i j s j + θ i
که می توان آن را به صورت زیر نمایش داد:
Δ E i = E i = o f f − E i = o n
با توجه به این موضوع که انرژی یک وضعیت در توزیع بولتسمان متناسب با منفی لگاریتم احتمال آن وضعیت است، انرژی دو وضعیت را در فرمول بالا جایگزین می کنیم:
Δ E i = − k B T l n ( p i = o f f ) − ( − k B T l n ( p i = o f f ) )
که k B ثابت بولتسمان است و در دما که همان T است خلاصه می شود:
Δ E i T = l n ( p i = o n ) − l n ( p i = o f f )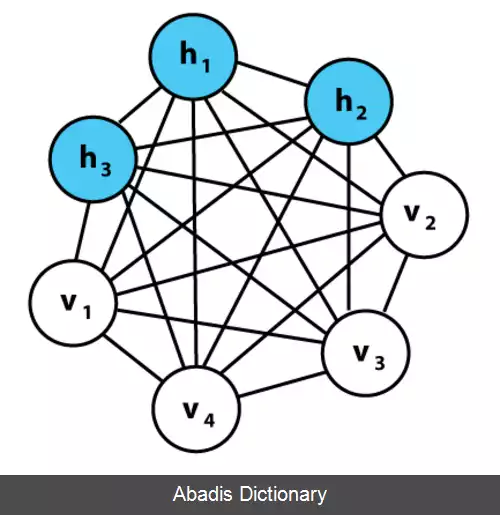
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفماشین های بولتسمان با ارتباطات های بدون محدودیت، معمولا برای حل مسائل عملی یادگیری ماشین مناسب نیستند، اما با محدود کردن صحیح ارتباطات در ماشین بولتسمان، می توان آن را برای حل مسئله های دنیای واقعی بهینه کرد. این ماشین به نام توزیع بولتسمان در مکانیک آماری نام گذاری شده است که در تابع نمونه گیری آنها استفاده می شود. نوع عمومی تر این مدل در یادگیری ماشین، مدل های مبتنی بر انرژی هستند. [ ۲]
ماشین بولتسمان، شبکه ای از واحد های دودویی است که یک مقدار "انرژی" دارد. وزن های ماشین بولتسمان تصادفی اند و مقدار انرژی ماشین از رابطه ی زیر به دست می آید:
E = − ( ∑ i < j w i j s i s j + ∑ i θ i s i )
که:
• w i j {\displaystyle w_{ij}} وزن ارتباط بین واحد های i {\displaystyle i} و j {\displaystyle j} است.
• s i {\displaystyle s_{i}} وضعیت واحد i {\displaystyle i} است. s i ∈ { 0 , 1 } {\displaystyle s_{i}\in \{0, 1\}}
• θ i {\displaystyle \theta _{i}} مقدار اریبی واحد i {\displaystyle i} است.
وزن ها را می توان به صورت یک ماتریس W = نشان داد که درایه های روی قطر اصلی آن صفر هستند.
تفاوت مقدار انرژی ماشین در دو حالت خاموش و روشن بودن یک واحد مشخص، که به صورت Δ E i نوشته می شود از رابطه ی زیر به دست آید:
Δ E i = ∑ i ≠ j w i j s j + θ i
که می توان آن را به صورت زیر نمایش داد:
Δ E i = E i = o f f − E i = o n
با توجه به این موضوع که انرژی یک وضعیت در توزیع بولتسمان متناسب با منفی لگاریتم احتمال آن وضعیت است، انرژی دو وضعیت را در فرمول بالا جایگزین می کنیم:
Δ E i = − k B T l n ( p i = o f f ) − ( − k B T l n ( p i = o f f ) )
که k B ثابت بولتسمان است و در دما که همان T است خلاصه می شود:
Δ E i T = l n ( p i = o n ) − l n ( p i = o f f )

wiki: ماشین بولتسمان
