لگاریتم

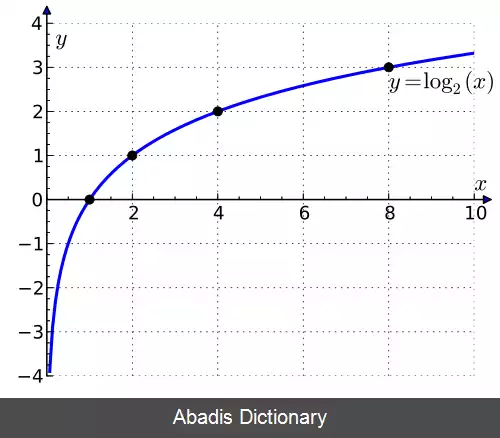
لُگاریتم[ ۱] ( به انگلیسی: Logarithm ) یک عدد در یک پایه، برابر با توانی از پایه است که آن عدد را می دهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلی تر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت log b ⁡ ( x ) = y نمایش می دهیم. مانند: log 10 ⁡ ( 1000 ) = 3 .
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیله ای برای آسان تر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسان تر کردن و سریع تر کردن محاسبه جدول های لگاریتم اعشاری و خطکش های لغزنده ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتم ها»، ساخته شده بودند:
مفهوم امروزی لگاریتم از تلاش های لئونارد اویلر در قرن ۱۸ گرفته شده است؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
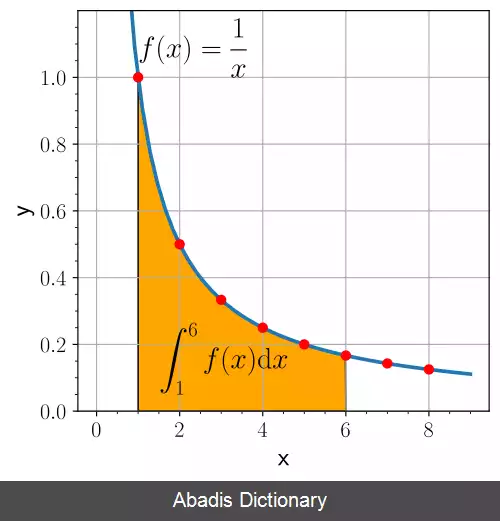
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری می نامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی می نامند. این لگاریتم در ریاضیات محض به ویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. لگاریتم دو دویی نیز در مبنای ۲ نوشته می شود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، می توان اندازه های بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسی بل یکایی لگاریتمی است که برای نشان دادن فشار صدا و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دادن میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان می شود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکل های هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن می توان به فاصله در موسیقی و رابطه های شمارش اعداد اول اشاره کردهمچنین در محاسبه زمان اجرای الگوریتم های برنامه های کامپیوتری استفاده می شود.
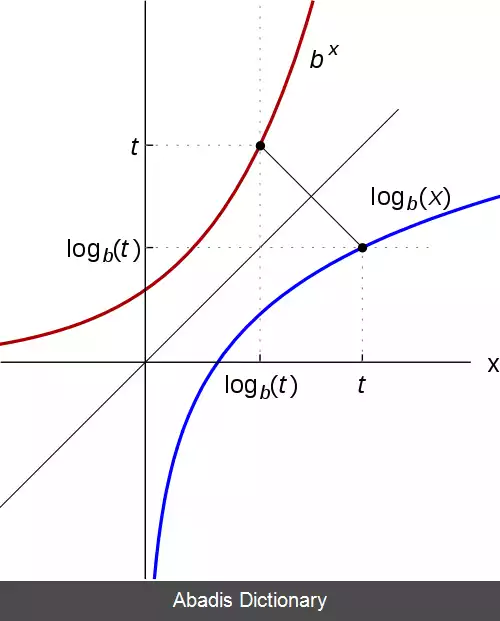
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده می شود.
انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بوده است. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ می شود.

لُگاریتم (logarithm)
لُگاریتم
نمای نشان دهندۀ عدد در پایهای معیّن. پایۀ لگاریتم متعارفی ۱۰ است. مثلاً لگاریتم ۱۰۰۰ در پایۀ ۱۰ برابر ۳ است، زیرا ۱۰ باید به توان ۳ برسد تا ۱۰۰۰ به دست آید. لگاریتم در این پایه۰.۳۰۱۰ است، زیرا ۳۰۱۰/۰ ۱۰=۲. جزء صحیح۲ لگاریتم را مفسّر و جزء کسری اعشاری آن را مانتیسمی گویند. پیش از عرضۀ حسابگرهای الکترونیک ارزان قیمت، به منظور ساده سازی محاسبات، به جای ضرب و تقسیم اعداد، لگاریتم های آن ها را جمع و تفریق می کردند، زیرا طبق قواعد لگاریتم،Log (xy) = Log x + Log yو (فرمول ۱)پس می توان لگاریتم هایx وy را جمع کرد و سپس آنتی لگاریتم جواب، یعنی عددی را که لگاریتم آن برابر جواب است، از جدول یافت.فرمول ۱:
جدول هایی برای لگاریتم و آنتی لگاریتم در دست اند که تبدیل اعداد به لگاریتم ها و بالعکس را نشان می دهند. مثلاً برای ضرب کردن ۶۵۶۰ در ۹۸۰، لگاریتم های آن ها،۳.۸۱۶۹ و۲.۹۹۱۲، را از جدول می یابیم و با هم جمع می کنیم. حاصل۶.۸۰۸۱ است. سپس، آنتی لگاریتم این عدد را که برابر با ۶,۴۲۸,۸۰۰ است می یابیم. پایۀ لگاریتم طبیعی یا نپری، عدد e، عددی گنگ و تقریباً برابر با۲.۷۱۸۳ است. اصل لگاریتم مبنای تهیۀ خط کش محاسبه بود. با رواج گستردۀ حسابگرهای الکترونیک جیبی، نیاز به لگاریتم کاهش یافت. نخستین جدول لگاریتم در پایۀ e را ریاضی دان اسکاتلندی، جان نپِر، در ۱۶۱۴ منتشر کرد. لگاریتم های در پایۀ ۱۰ را هنری بریگز انگلیسی (۱۵۶۱ـ۱۶۳۱) و آدریان ولاک هلندی (۱۶۰۰ـ۱۶۶۷) عرضه کردند.