در آنالیز مختلط، لم جردن، نتیجه ای است که از آن برایِ محاسبه ی انتگرال هایِ مسیر یا انتگرال هایِ ناسره، بهره می برند. استفاده از این لم، به خصوص با همراهیِ قضیه مانده صورت می گیرد. این لم به نامِ کامیل جردن، ریاضیدانِ فرانسوی، نامیده شده است.
مسیرِ دایره ایِ زیر را در نظر می گیریم:
با توجه به محدوده ی زاویه ها، این نیم دایره در نیم صفحه ی بالایی قرار دارد، مرکزِ آن مبداءِ مختصات است و R> 0 شعاعِ آن را نشان می دهد. حال تابعِ پیوسته ی f را که دامنه ی آن اعدادِ مختلط هستند با ضابطه ی زیر و بر رویِ این مسیر در نظر می گیریم:
که a> 0 است. لمِ جردن، لمی است که حدِ بالاییِ انتگرالِ f بر رویِ این مسیر را مشخص می کند. این حد برابر است با:
به شکلی مشابه، لمِ جردان برایِ نیم دایره ای که در نیم صفحه ی پایینی قرار گرفته نیز صادق است، اگر که a< 0 باشد.
• فرض کنید که به ازایِ تمامِ Rهایِ بزرگ، باز هم f بر رویِ نیم دایره ی CR تعریف شده و بر رویِ آن پیوسته باشد، در این صورت اگر مقدارِ ماکزیمم تابع در Rهایِ بزرگ به سمتِ صفر میل کند ( به این شرط، شرطِ ( * ) می گوییم. ) :
• اگر a=0 باشد، آن گاه لمِ تخمین ( به انگلیسی: Estimation lemma ) برقرار است. در صورتی که شرطِ ( * ) برقرار باشد، حتی اگر a=0 باشد، باز هم در R → ∞ {\displaystyle {R\to \infty }} ، مقدارِ انتگرال برابر صفر می شود. اما در موقعیت هایی که شرطِ ( * ) برقرار نیست، برایِ پیدا کردنِ حدِ بالایِ انتگرال باید به لمِ تخمین مراجعه کرد.
• همانندِ لمِ تخمین، حدِ بالایی ای که لمِ جردن مشخص می کند، به شکلِ صریح به طولِ CR ارتباط ندارد و مستقل از شعاعِ مسیر است.
لمِ جردن، در محاسبه ی انتگرال هایِ حقیقی که بر رویِ محورِ اعدادِ حقیقی تعریف می شوند می تواند بسیار مفید باشد. تابعِ
را در نظر می گیریم که در نیمه ی بالاییِ صفحه ی اعدادِ مختلط، همه جا هولومورفیک ( تحلیلی ) و پیوسته است مگر در تعدادِ متناهی نقطه و این نقطه ها را که هیچ کدام بر رویِ محورِ اعدادِ حقیقی قرار ندارند، با z1 و z2 و . . . تا zn نمایش می دهیم. مسیرِ بسته ی C را که در شکل نشان داده شد در نظر بگیرید، این مسیر از اجتماعِ مسیرهایِ C1 و C2 تشکیل می شود و بنا به تعریف داریم:
اما بر رویِ مسیرِ C2، از آن جایی که متغیرِ Z، تنها شاملِ عددهایِ حقیقی می شود، به جایِ متغیرِ z می توان تنها بخشِ حقیقیِ آن را قرار داد و در نتیجه انتگرالِ دوم، به انتگرالِ حقیقیِ معمولی تبدیل می شود: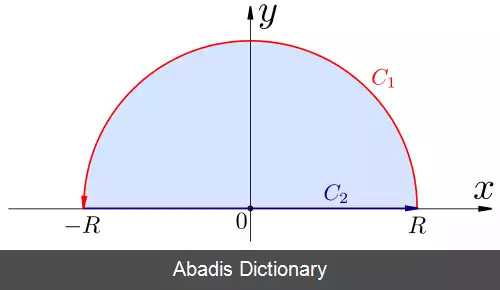
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمسیرِ دایره ایِ زیر را در نظر می گیریم:
با توجه به محدوده ی زاویه ها، این نیم دایره در نیم صفحه ی بالایی قرار دارد، مرکزِ آن مبداءِ مختصات است و R> 0 شعاعِ آن را نشان می دهد. حال تابعِ پیوسته ی f را که دامنه ی آن اعدادِ مختلط هستند با ضابطه ی زیر و بر رویِ این مسیر در نظر می گیریم:
که a> 0 است. لمِ جردن، لمی است که حدِ بالاییِ انتگرالِ f بر رویِ این مسیر را مشخص می کند. این حد برابر است با:
به شکلی مشابه، لمِ جردان برایِ نیم دایره ای که در نیم صفحه ی پایینی قرار گرفته نیز صادق است، اگر که a< 0 باشد.
• فرض کنید که به ازایِ تمامِ Rهایِ بزرگ، باز هم f بر رویِ نیم دایره ی CR تعریف شده و بر رویِ آن پیوسته باشد، در این صورت اگر مقدارِ ماکزیمم تابع در Rهایِ بزرگ به سمتِ صفر میل کند ( به این شرط، شرطِ ( * ) می گوییم. ) :
• اگر a=0 باشد، آن گاه لمِ تخمین ( به انگلیسی: Estimation lemma ) برقرار است. در صورتی که شرطِ ( * ) برقرار باشد، حتی اگر a=0 باشد، باز هم در R → ∞ {\displaystyle {R\to \infty }} ، مقدارِ انتگرال برابر صفر می شود. اما در موقعیت هایی که شرطِ ( * ) برقرار نیست، برایِ پیدا کردنِ حدِ بالایِ انتگرال باید به لمِ تخمین مراجعه کرد.
• همانندِ لمِ تخمین، حدِ بالایی ای که لمِ جردن مشخص می کند، به شکلِ صریح به طولِ CR ارتباط ندارد و مستقل از شعاعِ مسیر است.
لمِ جردن، در محاسبه ی انتگرال هایِ حقیقی که بر رویِ محورِ اعدادِ حقیقی تعریف می شوند می تواند بسیار مفید باشد. تابعِ
را در نظر می گیریم که در نیمه ی بالاییِ صفحه ی اعدادِ مختلط، همه جا هولومورفیک ( تحلیلی ) و پیوسته است مگر در تعدادِ متناهی نقطه و این نقطه ها را که هیچ کدام بر رویِ محورِ اعدادِ حقیقی قرار ندارند، با z1 و z2 و . . . تا zn نمایش می دهیم. مسیرِ بسته ی C را که در شکل نشان داده شد در نظر بگیرید، این مسیر از اجتماعِ مسیرهایِ C1 و C2 تشکیل می شود و بنا به تعریف داریم:
اما بر رویِ مسیرِ C2، از آن جایی که متغیرِ Z، تنها شاملِ عددهایِ حقیقی می شود، به جایِ متغیرِ z می توان تنها بخشِ حقیقیِ آن را قرار داد و در نتیجه انتگرالِ دوم، به انتگرالِ حقیقیِ معمولی تبدیل می شود:

wiki: لم جردن
