در حساب گزاره ای و جبر بولی، قوانین دمورگان ( به انگلیسی: De Morgan's Laws ) ، [ ۱] [ ۲] [ ۳] یک جفت قواعد تبدیل اند که هردو قواعد استنتاجی معتبری می باشند. این تبدیل ها را براساس نام آگوستوس دمورگان نامگذاری کرده اند که یک ریاضی دان بریتانیایی قرن ۱۹م میلادی است. این قواعد امکان می دهند تا عطف و فصل به طور محض، از طریق نقیض بیان شوند.
این قواعد را به زبان فارسی می توان به این صورت بیان کرد:
• نقیض فصل، عطف نقیض هاست.
• نقیض عطف، فصل نقیض هاست.
یا
• متمم اجتماع دو مجموعه، همان اشتراک متمم هایشان است.
• متمم اشتراک دو مجموعه، همان اجتماع متمم هایشان است.
• نقیض ( A یا B ) = نقیض A و نقیض B
• نقیض ( A و B ) = نقیض A یا نقیض B
در نظریه مجموعه ها و جبر بولی، این عبارات را می توان به صورت زیر نوشت:
که در آن:
• A {\displaystyle A} و B {\displaystyle B} مجموعه هستند
• A ¯ {\displaystyle {\overline {A}}} متمم A {\displaystyle A} است
• ∩ {\displaystyle \cap } اشتراک است
• ∪ {\displaystyle \cup } اجتماع است.
این قواعد را برحسب زبان صوری می توان به صورت زیر نوشت:
¬ ( P ∨ Q ) ⟺ ( ¬ P ) ∧ ( ¬ Q )
و
¬ ( P ∧ Q ) ⟺ ( ¬ P ) ∨ ( ¬ Q )
• P و Q گزاره هستند
• ¬ {\displaystyle \neg } عملگر نقیض منطقی است ( NOT )
• ∧ {\displaystyle \land } عملگر منطقی عطف است ( AND )
• ∨ {\displaystyle \lor } عملگر منطقی فصل است ( OR )
• ⟺ {\displaystyle \iff } نماد فرامنطقی است که معنای آن اینگونه است: «می توان آن را در یک اثبات صوری جایگزین کرد با»
کاربردهای این قواعد منطقی شامل عبارات منطقی در برنامه های کامپیوتری و طراحی مدارهای دیجیتالی است. قواعد دمورگان مثالی از مفهوم کلی تری از دوگان ریاضیاتی است.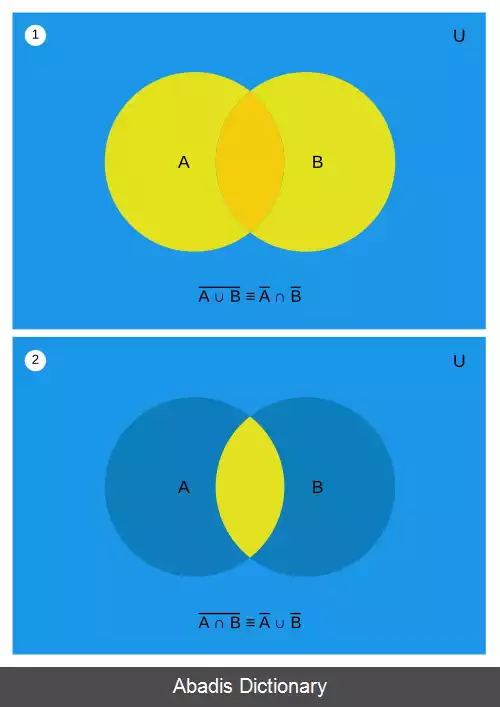

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قواعد را به زبان فارسی می توان به این صورت بیان کرد:
• نقیض فصل، عطف نقیض هاست.
• نقیض عطف، فصل نقیض هاست.
یا
• متمم اجتماع دو مجموعه، همان اشتراک متمم هایشان است.
• متمم اشتراک دو مجموعه، همان اجتماع متمم هایشان است.
• نقیض ( A یا B ) = نقیض A و نقیض B
• نقیض ( A و B ) = نقیض A یا نقیض B
در نظریه مجموعه ها و جبر بولی، این عبارات را می توان به صورت زیر نوشت:
که در آن:
• A {\displaystyle A} و B {\displaystyle B} مجموعه هستند
• A ¯ {\displaystyle {\overline {A}}} متمم A {\displaystyle A} است
• ∩ {\displaystyle \cap } اشتراک است
• ∪ {\displaystyle \cup } اجتماع است.
این قواعد را برحسب زبان صوری می توان به صورت زیر نوشت:
¬ ( P ∨ Q ) ⟺ ( ¬ P ) ∧ ( ¬ Q )
و
¬ ( P ∧ Q ) ⟺ ( ¬ P ) ∨ ( ¬ Q )
• P و Q گزاره هستند
• ¬ {\displaystyle \neg } عملگر نقیض منطقی است ( NOT )
• ∧ {\displaystyle \land } عملگر منطقی عطف است ( AND )
• ∨ {\displaystyle \lor } عملگر منطقی فصل است ( OR )
• ⟺ {\displaystyle \iff } نماد فرامنطقی است که معنای آن اینگونه است: «می توان آن را در یک اثبات صوری جایگزین کرد با»
کاربردهای این قواعد منطقی شامل عبارات منطقی در برنامه های کامپیوتری و طراحی مدارهای دیجیتالی است. قواعد دمورگان مثالی از مفهوم کلی تری از دوگان ریاضیاتی است.


wiki: قوانین دمورگان
