در هندسه، قطعه کروی جامدی است که با بریدن یک کره یا یک توپ با یک جفت موازی تعریف می شود. صفحه های موازی را می توان آن را به عنوان یک کلاهک کروی در نظر گرفت که قسمت بالایی آن کوتاه شده است، و بنابراین با کلاهک کروی مطابقت دارد.
سطح "قطعه کروی" ( به استثنای پایه ها ) "منطقه کروی" نامیده می شود. اگر شعاع کره R نامیده شود، شعاع پایه های قطعه کروی r1 و r2، و ارتفاع پاره ( فاصله یک صفحه موازی تا صفحه موازی ) به نام hاست.
سپس حجم از بخش کروی اینگونه است: V = π h 6 ( 3 r 1 2 + 3 r 2 2 + h 2 ) .
منحنی سطح ناحیه کروی - که پایه های بالا و پایین را بر می دارد برابر با رابطه زیر است:
A = 2 π R h .
برای محاسبه حجم و مساحت یک برش کروی، فرمول های زیر اعمال می شود. r نشان دهنده شعاع کره، a 1 , a 2 شعاع دایره های مرزی و h ارتفاع لایه کروی است. . این سه کمیت مستقل از یکدیگر نیستند.
لایه کره را می توان به عنوان قطعه کره S 1 با دایره پایینی به عنوان دایره پایه، و قطعه کره S 2 با قسمت بالایی در نظر گرفت. ] همانطور که دایره پایه برداشته می شود. بگذارید h 1 ارتفاع S 1 باشد و h 2 ارتفاع شکست در تجزیه ( خطای نحوی ) : {\displaystyle S_2< / ریاضی> . ] دو بخش کره هستند : < math> V_1 = \frac{\pi}{3} \cdot h_1^2 \cdot ( 3 \cdot r - h_1 ) } : V 2 = π 3 ⋅ h 2 2 ⋅ ( 3 ⋅ r − h 2 ) قطعه کروی را نیز ببینید. همینطور است : V = V 1 − V 2 = π 3 ⋅ ( 3 ⋅ ( h 1 2 − h 2 2 ) ⋅ r − ( h 1 3 − h 2 3 ) ) = π 3 ⋅ ( h 1 − h 2 ) ⋅ ( 3 ⋅ ( h 1 + h 2 ) ⋅ r − ( h 1 2 + h 1 ⋅ h 2 + h 2 2 ) ) با روابط 2 ⋅ r ⋅ h 1 = a 1 2 + h 1 2 , 2 ⋅ r ⋅ h 2 = a 2 2 + h 2 2 ( به مراجعه کنید] ) تسلیم شد : شکست در تجزیه ( تابع ناشناختهٔ ' \begin{align}' ) : {\displaystyle \begin{align} V & = \frac{\pi}{3} \cdot ( h_1 - h_2 ) \cdot \left ( \frac{3}{2} \cdot ( a_1^2 + h_1^2 + a_2^2 + h_2^2 ) - h_1^2 - h_1 \cdot h_2 - h_2^2\راست ) \\ & = \frac{\pi}{6} \cdot ( h_1 - h_2 ) \cdot ( 3 \cdot ( a_1^2 + a_2^2 ) + ( h_1 - h_2 ) ^2 ) \end{align} } از آنجایی که h = h 1 − h 2 ، فرمول فوق به شرح زیر است: V = π 6 ⋅ h ⋅ ( 3 ⋅ a 1 2 + 3 ⋅ a 2 2 + h 2 ) برای سطح نتیجه مشابه است : M = M 1 − M 2 = 2 ⋅ π ⋅ r ⋅ h 1 − 2 ⋅ π ⋅ r ⋅ h 2 = 2 ⋅ π ⋅ r ⋅ ( h 1 − h 2 ) = 2 ⋅ π ⋅ r ⋅ h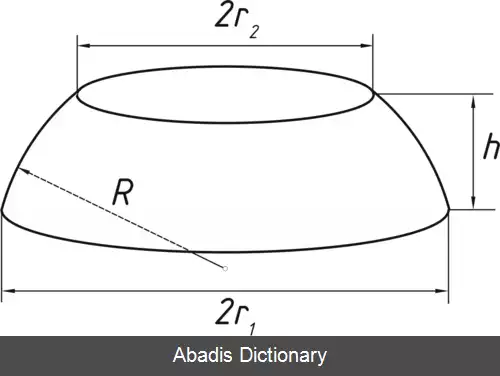

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفسطح "قطعه کروی" ( به استثنای پایه ها ) "منطقه کروی" نامیده می شود. اگر شعاع کره R نامیده شود، شعاع پایه های قطعه کروی r1 و r2، و ارتفاع پاره ( فاصله یک صفحه موازی تا صفحه موازی ) به نام hاست.
سپس حجم از بخش کروی اینگونه است: V = π h 6 ( 3 r 1 2 + 3 r 2 2 + h 2 ) .
منحنی سطح ناحیه کروی - که پایه های بالا و پایین را بر می دارد برابر با رابطه زیر است:
A = 2 π R h .
برای محاسبه حجم و مساحت یک برش کروی، فرمول های زیر اعمال می شود. r نشان دهنده شعاع کره، a 1 , a 2 شعاع دایره های مرزی و h ارتفاع لایه کروی است. . این سه کمیت مستقل از یکدیگر نیستند.
لایه کره را می توان به عنوان قطعه کره S 1 با دایره پایینی به عنوان دایره پایه، و قطعه کره S 2 با قسمت بالایی در نظر گرفت. ] همانطور که دایره پایه برداشته می شود. بگذارید h 1 ارتفاع S 1 باشد و h 2 ارتفاع شکست در تجزیه ( خطای نحوی ) : {\displaystyle S_2< / ریاضی> . ] دو بخش کره هستند : < math> V_1 = \frac{\pi}{3} \cdot h_1^2 \cdot ( 3 \cdot r - h_1 ) } : V 2 = π 3 ⋅ h 2 2 ⋅ ( 3 ⋅ r − h 2 ) قطعه کروی را نیز ببینید. همینطور است : V = V 1 − V 2 = π 3 ⋅ ( 3 ⋅ ( h 1 2 − h 2 2 ) ⋅ r − ( h 1 3 − h 2 3 ) ) = π 3 ⋅ ( h 1 − h 2 ) ⋅ ( 3 ⋅ ( h 1 + h 2 ) ⋅ r − ( h 1 2 + h 1 ⋅ h 2 + h 2 2 ) ) با روابط 2 ⋅ r ⋅ h 1 = a 1 2 + h 1 2 , 2 ⋅ r ⋅ h 2 = a 2 2 + h 2 2 ( به مراجعه کنید] ) تسلیم شد : شکست در تجزیه ( تابع ناشناختهٔ ' \begin{align}' ) : {\displaystyle \begin{align} V & = \frac{\pi}{3} \cdot ( h_1 - h_2 ) \cdot \left ( \frac{3}{2} \cdot ( a_1^2 + h_1^2 + a_2^2 + h_2^2 ) - h_1^2 - h_1 \cdot h_2 - h_2^2\راست ) \\ & = \frac{\pi}{6} \cdot ( h_1 - h_2 ) \cdot ( 3 \cdot ( a_1^2 + a_2^2 ) + ( h_1 - h_2 ) ^2 ) \end{align} } از آنجایی که h = h 1 − h 2 ، فرمول فوق به شرح زیر است: V = π 6 ⋅ h ⋅ ( 3 ⋅ a 1 2 + 3 ⋅ a 2 2 + h 2 ) برای سطح نتیجه مشابه است : M = M 1 − M 2 = 2 ⋅ π ⋅ r ⋅ h 1 − 2 ⋅ π ⋅ r ⋅ h 2 = 2 ⋅ π ⋅ r ⋅ ( h 1 − h 2 ) = 2 ⋅ π ⋅ r ⋅ h


wiki: قطعه کروی
