قضیه گرین، یکی از قضایای پر کاربرد در علم حساب دیفرانسیل و انتگرال است که انتگرال خطی منحنی بسته را به انتگرال دو گانه تبدیل می کند . نام این نظریه از نام جرج گرین گرفته شده است.
فرض کنیم که C منحنی ساده و بسته در صفحهٔ XY بوده و D ناحیه محدود و کراندار بین منحنی C باشد. اگر L و M توابعی از دو متغیر x و y بوده و در میدان D پیوسته و دارای مشتق جزئی مرتبه اول باشند، داریم: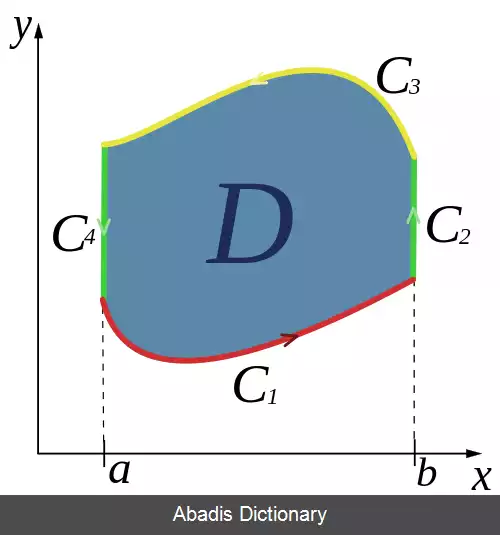
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنیم که C منحنی ساده و بسته در صفحهٔ XY بوده و D ناحیه محدود و کراندار بین منحنی C باشد. اگر L و M توابعی از دو متغیر x و y بوده و در میدان D پیوسته و دارای مشتق جزئی مرتبه اول باشند، داریم:

wiki: قضیه گرین
