در نظریه مجموعه های مقدماتی، قضیه کانتور نتیجه بنیادینی است که بیان می دارد: برای هر مجموعه A ، مجموعه تمام زیر مجموعه های A ( به آن مجموعه توانی A گفته می شود و با P ( A ) نمایش داده می شود ) به طور اکید کاردینالی بزرگتر از خود A دارد. برای مجموعه های متناهی می توان با شمردن تعداد زیر مجموعه ها، درستی قضیه کانتور را مشاهده کرد. با در نظر گرفتن تهی به عنوان یک زیر مجموعه، کل زیرمجموعه های یک مجموعه n عضوی برابر 2 n خواهد بود، بنابر این اگر c a r d ( A ) = n ، آنگاه c a r d ( P ( A ) ) = 2 n ، و قضیه برقرار است چون برای تمام اعداد صحیح نامنفی داریم 2 n > n .
کشف مهم کانتور این بود که گزاره اخیر برای هر مجموعه ای درست است، یعنی علاوه بر مجموعه های متناهی برای مجموعه های نامتناهی، چه شمارا یا ناشمارا نیز درست است. به طور خاص، یکی از پیامدهای مهم قضیه کانتور این است که اعداد طبیعی که یک مجموعه شمارا با کاردینال ℵ 0 = c a r d ( N ) است، برابر یک مجموعه ناشمارا می باشد که کاردینال آن با اعداد حقیقی برابر بوده و این کاردینال از کاردینال اعداد طبیعی بزرگتر است و به آن کاردینال پیوستار گویند: c a r d ( R ) = c a r d ( P ( N ) ) . رابطه بین این کاردینال ها را به این صورت نمایش می دهند: c = 2 ℵ 0 > ℵ 0 .
این قضیه به افتخار ریاضیدان آلمانی گئورگ کانتور نامگذاری کردند، او اولین کسی بود که این قضیه را در انتهای قرن نوزدهم میلادی بیان و اثبات کرد. قضیه کانتور پیامدهای فوری و مهمی در فلسفه ریاضیات داشت. به عنوان مثال، با تکرار عمل ساخت مجموعه توانی از یک مجموعه نامتناهی و اعمال قضیه کانتور، به سلسله مراتب نامتناهی از کاردینال های نامتناهی می رسیم که هر کدام از قبلی به طور اکید بزرگتر است. در نهایت، این قضیه دلالت بر این دارد که هیچ کاردینالی که از همه کاردینال ها بزرگتر باشد وجود ندارد ( به زبان دیگر "بزرگترین بی نهایت وجود ندارد" ) .
f یک تابع از A به مجموعه توانی A است. برای برقراری نظریه کانتور باید اثبات شود که f الزاماً پوشا نیست. برای انجام این امر، کافی است یک عنصر مجموعه توانی از A که یک زیرمجموعه از A است ارائه کرده و اثبات کنیم که در برد f وجود ندارد. چنین زیرمجموعه ای می تواند به صورت زیر ساخته شود.
این بدین معناست که بنا بر تعریف، برای هر x عضو x، A عضو B است اگر و و فقط اگر x عضو f نباشد. پس به ازای تمام xها مجموعه های B و ( f ( x فرق می کنند. هیچ x ای یافت نمی شود که f ( x ) =B به عبارت دیگر B در برد f نیست. به خاطر اینکه x دو بار در عبارت بالا حضور پیدا کرده، ( ( x عضو f ( x ) این یک عبارت قطری است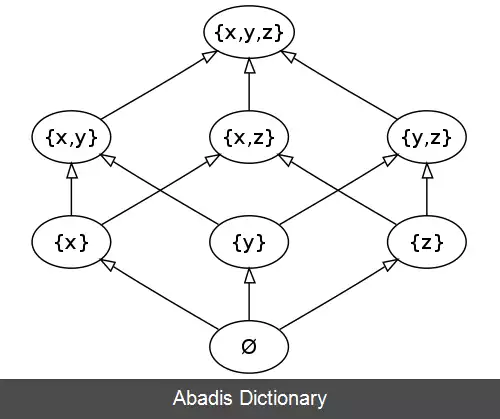

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکشف مهم کانتور این بود که گزاره اخیر برای هر مجموعه ای درست است، یعنی علاوه بر مجموعه های متناهی برای مجموعه های نامتناهی، چه شمارا یا ناشمارا نیز درست است. به طور خاص، یکی از پیامدهای مهم قضیه کانتور این است که اعداد طبیعی که یک مجموعه شمارا با کاردینال ℵ 0 = c a r d ( N ) است، برابر یک مجموعه ناشمارا می باشد که کاردینال آن با اعداد حقیقی برابر بوده و این کاردینال از کاردینال اعداد طبیعی بزرگتر است و به آن کاردینال پیوستار گویند: c a r d ( R ) = c a r d ( P ( N ) ) . رابطه بین این کاردینال ها را به این صورت نمایش می دهند: c = 2 ℵ 0 > ℵ 0 .
این قضیه به افتخار ریاضیدان آلمانی گئورگ کانتور نامگذاری کردند، او اولین کسی بود که این قضیه را در انتهای قرن نوزدهم میلادی بیان و اثبات کرد. قضیه کانتور پیامدهای فوری و مهمی در فلسفه ریاضیات داشت. به عنوان مثال، با تکرار عمل ساخت مجموعه توانی از یک مجموعه نامتناهی و اعمال قضیه کانتور، به سلسله مراتب نامتناهی از کاردینال های نامتناهی می رسیم که هر کدام از قبلی به طور اکید بزرگتر است. در نهایت، این قضیه دلالت بر این دارد که هیچ کاردینالی که از همه کاردینال ها بزرگتر باشد وجود ندارد ( به زبان دیگر "بزرگترین بی نهایت وجود ندارد" ) .
f یک تابع از A به مجموعه توانی A است. برای برقراری نظریه کانتور باید اثبات شود که f الزاماً پوشا نیست. برای انجام این امر، کافی است یک عنصر مجموعه توانی از A که یک زیرمجموعه از A است ارائه کرده و اثبات کنیم که در برد f وجود ندارد. چنین زیرمجموعه ای می تواند به صورت زیر ساخته شود.
این بدین معناست که بنا بر تعریف، برای هر x عضو x، A عضو B است اگر و و فقط اگر x عضو f نباشد. پس به ازای تمام xها مجموعه های B و ( f ( x فرق می کنند. هیچ x ای یافت نمی شود که f ( x ) =B به عبارت دیگر B در برد f نیست. به خاطر اینکه x دو بار در عبارت بالا حضور پیدا کرده، ( ( x عضو f ( x ) این یک عبارت قطری است


wiki: قضیه کانتور
