در هندسه اقلیدسی، قضیه پرچم بریتانیا بیان می دارد که اگر یک نقطه دلخواه P در داخل مستطیل ABCD انتخاب شود، مجموع مربعات فاصله اقلیدسی از P تا دو رأس مقابل مستطیل برابر است با فاصله اقلیدسی از P تا دو رأس مقابل دیگر. [ ۱] [ ۲] [ ۳]
این قضیه همچنین در مورد نقاط خارج از مستطیل و به طور کلی در مورد فاصله های یک نقطه در فضای اقلیدسی تا رئوس یک مستطیل در فضا صادق است. [ ۴] [ ۵]
این قضیه را می توان به عنوان تعمیم قضیه فیثاغورس نیز در نظر گرفت. قرار دادن نقطه P بر روی هر یک از چهار رأس مستطیل باعث می شود که مربع اندازه قطر مستطیل برابر با مجموع مربعات عرض و طول مستطیل باشد.
P = D : A B 2 + 0 = A C 2 + C B 2
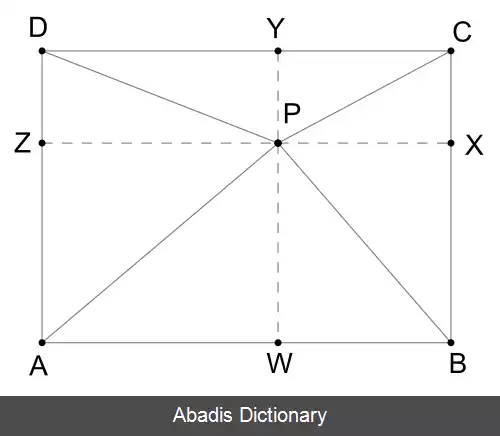
همان طور که در شکل نشان داده شده است، خطوط عمود از نقطه P به اضلاع مستطیل، اضلاع AB , BC , CD و AD را به ترتیب در نقاط W , X، Y و Z قطع می کند. با اعمال قضیه فیثاغورس به مثلث AWP، داریم: WP = AZ، نتیجه می شود که
• A P 2 = A W 2 + W P 2 = A W 2 + A Z 2 {\displaystyle AP^{2}=AW^{2}+WP^{2}=AW^{2}+AZ^{2}}
و با استدلال مشابه مربعات طول فواصل P تا سه رأس دیگر را می توان به صورت زیر محاسبه کرد:
• P C 2 = W B 2 + Z D 2 , {\displaystyle PC^{2}=WB^{2}+ZD^{2}, }
• B P 2 = W B 2 + A Z 2 , {\displaystyle BP^{2}=WB^{2}+AZ^{2}, }
• P D 2 = Z D 2 + A W 2 . {\displaystyle PD^{2}=ZD^{2}+AW^{2}. }
از این رو:
این قضیه نام خود را از این فرایندی گرفته است که وقتی پاره خط ها از P تا رئوس مستطیل ترسیم می شوند، همراه با خطوط عمود بر اضلاع ترسیم شده در اثبات، شکل کامل شده تا حدودی شبیه پرچم بریتانیا است.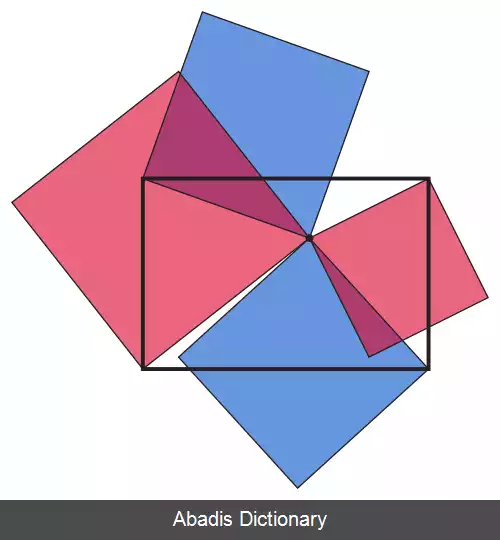
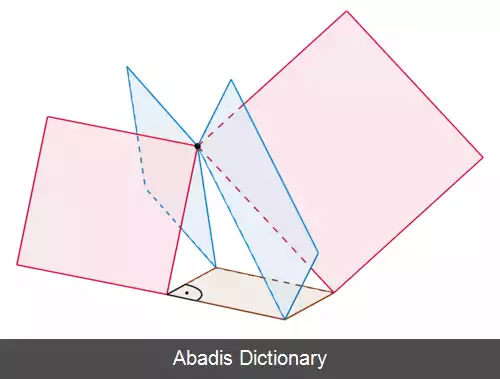

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین قضیه همچنین در مورد نقاط خارج از مستطیل و به طور کلی در مورد فاصله های یک نقطه در فضای اقلیدسی تا رئوس یک مستطیل در فضا صادق است. [ ۴] [ ۵]
این قضیه را می توان به عنوان تعمیم قضیه فیثاغورس نیز در نظر گرفت. قرار دادن نقطه P بر روی هر یک از چهار رأس مستطیل باعث می شود که مربع اندازه قطر مستطیل برابر با مجموع مربعات عرض و طول مستطیل باشد.
P = D : A B 2 + 0 = A C 2 + C B 2
همان طور که در شکل نشان داده شده است، خطوط عمود از نقطه P به اضلاع مستطیل، اضلاع AB , BC , CD و AD را به ترتیب در نقاط W , X، Y و Z قطع می کند. با اعمال قضیه فیثاغورس به مثلث AWP، داریم: WP = AZ، نتیجه می شود که
• A P 2 = A W 2 + W P 2 = A W 2 + A Z 2 {\displaystyle AP^{2}=AW^{2}+WP^{2}=AW^{2}+AZ^{2}}
و با استدلال مشابه مربعات طول فواصل P تا سه رأس دیگر را می توان به صورت زیر محاسبه کرد:
• P C 2 = W B 2 + Z D 2 , {\displaystyle PC^{2}=WB^{2}+ZD^{2}, }
• B P 2 = W B 2 + A Z 2 , {\displaystyle BP^{2}=WB^{2}+AZ^{2}, }
• P D 2 = Z D 2 + A W 2 . {\displaystyle PD^{2}=ZD^{2}+AW^{2}. }
از این رو:
این قضیه نام خود را از این فرایندی گرفته است که وقتی پاره خط ها از P تا رئوس مستطیل ترسیم می شوند، همراه با خطوط عمود بر اضلاع ترسیم شده در اثبات، شکل کامل شده تا حدودی شبیه پرچم بریتانیا است.




wiki: قضیه پرچم بریتانیا
