در ریاضیات، ساده ترین حالت از قانون متوازی الأضلاع ( که به آن اتحاد متوازی الأضلاع نیز گفته می شود ) متعلق به هندسه مسطحه مقدماتیست. این قانون بیان می دارد که جمع مربع چهار ضلع متوازی الأضلاع برابر جمع مربع اضلاع دو قطر آن است. ما اضلاع را با این نماد گذاری نمایش می دهیم: A B , B C , C D , D A . اما از آنجا که در، اضلاع مقابل هم در یک متوازی الأضلاع لزوماً با هم برابرند، یعنی A B = C D و B C = D A ، این قانون را می توان به صورت زیر بیان نمود:
اگر متوازی الاضلاع تبدیل به یک مستطیل گردد ( چرا که مستطیل حالت خاصی از متوازی الأضلاع است ) ، طول دو قطر آن با هم برابر شده A C = B C ، لذا در این حالت خواهیم داشت:
که همان قضیه فیثاغورث است. برای چهار ضلعی های کلی تر که در آن ها اضلاع مقابل هم لزوماً موازی نیستند داریم:
که در آن x طول پاره خط متصل کنندهٔ میانه های قطرهاست. می توان از شکل مشاهده کرد برای حالت متوازی الأضلاع، x = 0 بوده و اتحاد فوق در این حالت به همان قانون متوازی الأضلاع که ذکر آن رفت تبدیل می شود.
در متوازی الأضلاع سمت چپ، داریم: A D = B C = a , A B = D C = b , ∠ B A D = α . با استفاده از قانون کسینوس ها در مثلث △ B A D ، بدست می آوریم:
a 2 + b 2 − 2 a b cos ( α ) = B D 2
در متوازی الأضلاع، زاویه های مجاور مکمل اند، لذا داریم ∠ A D C = 180 deg − α . با استفاده از قانون کسینوس ها در مثلث △ A D C بدست می آوریم:
a 2 + b 2 − 2 a b cos ( 180 ∘ − α ) = A C 2
با اعمال اتحاد مثلثاتی cos ( 180 ∘ − x ) = − cos x به سمت چپ عبارت بالا، به معادلهٔ زیر می رسیم:
a 2 + b 2 + 2 a b cos ( α ) = A C 2
اکنون جمع مربعات B D 2 + A C 2 برابر خواهد بود با:
B D 2 + A C 2 = a 2 + b 2 − 2 a b cos ( α ) + a 2 + b 2 + 2 a b cos ( α )
که بعد از ساده سازی به عبارت زیر می رسیم:
B D 2 + A C 2 = 2 a 2 + 2 b 2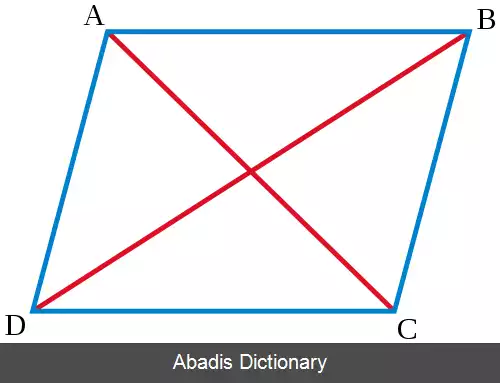

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر متوازی الاضلاع تبدیل به یک مستطیل گردد ( چرا که مستطیل حالت خاصی از متوازی الأضلاع است ) ، طول دو قطر آن با هم برابر شده A C = B C ، لذا در این حالت خواهیم داشت:
که همان قضیه فیثاغورث است. برای چهار ضلعی های کلی تر که در آن ها اضلاع مقابل هم لزوماً موازی نیستند داریم:
که در آن x طول پاره خط متصل کنندهٔ میانه های قطرهاست. می توان از شکل مشاهده کرد برای حالت متوازی الأضلاع، x = 0 بوده و اتحاد فوق در این حالت به همان قانون متوازی الأضلاع که ذکر آن رفت تبدیل می شود.
در متوازی الأضلاع سمت چپ، داریم: A D = B C = a , A B = D C = b , ∠ B A D = α . با استفاده از قانون کسینوس ها در مثلث △ B A D ، بدست می آوریم:
a 2 + b 2 − 2 a b cos ( α ) = B D 2
در متوازی الأضلاع، زاویه های مجاور مکمل اند، لذا داریم ∠ A D C = 180 deg − α . با استفاده از قانون کسینوس ها در مثلث △ A D C بدست می آوریم:
a 2 + b 2 − 2 a b cos ( 180 ∘ − α ) = A C 2
با اعمال اتحاد مثلثاتی cos ( 180 ∘ − x ) = − cos x به سمت چپ عبارت بالا، به معادلهٔ زیر می رسیم:
a 2 + b 2 + 2 a b cos ( α ) = A C 2
اکنون جمع مربعات B D 2 + A C 2 برابر خواهد بود با:
B D 2 + A C 2 = a 2 + b 2 − 2 a b cos ( α ) + a 2 + b 2 + 2 a b cos ( α )
که بعد از ساده سازی به عبارت زیر می رسیم:
B D 2 + A C 2 = 2 a 2 + 2 b 2


wiki: قانون متوازی الاضلاع
