قانون لگاریتم های تکراری، اولین بار توسط A. Y. Khinchin[ ۱] ( به فارسی: خینچین ) در سال ۱۹۲۴ و بعدها، در سال ۱۹۲۹ به وسیله A. N. Kolmogorov[ ۲] ( به فارسی: کولموگوروف ) به صورت کاملتری بیان شد. همچنین ریشه این قانون به یک مسئله خاص در نظریه اعداد بازمی گردد. [ ۳]
از قانون Hewitt - Savage 0 - 1 ( به فارسی: هویت سوج ) می دانیم اگر X 1 , X 2 , . . . , X n متغیرهای تصادفی حقیقی با توزیع متقارن حول 0 باشند و S n = ∑ j = 1 n X j باشد، آنگاه داریم: − ∞ = lim inf n → ∞ S n < lim sup n → ∞ S n = ∞ که منظور از lim sup n → ∞ S n و lim inf n → ∞ S n به ترتیب حد سوپریمم و حد اینفیمم است. [ ۴] حال اگر بخواهیم کمی دقیقتر عبارت بالا را توسعه دهیم، باید از قانون Hartman - Wintner ( به فارسی: هارتمن وینتنر ) استفاده کنیم که بیان می کند:
lim inf n → ∞ S n − ϕ ( n ) = lim sup n → ∞ S n ϕ ( n ) = 1 a l m o s t s u r e l y و برای هر S n ای که شرایط زیر را داشته باشد: { E = 0 V a r = σ 2 = f i n i t e داریم:[ ۵]
lim sup n → ∞ S n 2 σ 2 n log log ( n ) = 1 a l m o s t s u r e l y برای درک بهتر مطالب بالا به شکل روبرو توجه کنید. سری را در نظر بگیرید که در آن ، امین رقم اعشاری عدد در سیستم دودویی است. دو نمودار ( نقطه چین ) و ( خط پررنگ ) رسم شده است و به وضوح می توان دید که وقتی n ⟶ ∞ این دو نمودار به هم همگرا می شوند. مثال فرض کنید با دوستتان سنگ، کاغذ، قیچی بازی می کنید به طوری که شما به احتمال ۱/۳ برنده می شوید، به احتمال ۱/۳ بازنده اید و به احتمال ۱/۳ کسی برنده نمی شود. اگر برنده شوید ۱ ریال دریافت می کنید، اگر بازنده شوید ۱ ریال به دوستتان می دهید و اگر کسی برنده نشود هیچ اتفاقی نمی افتد.
متغیر تصادفی X n را مقدار پولی در نظر بگیرید که در مرحله n ام بازی باید بپردازید به این ترتیب برای متغیر تصادفی مقادیر زیر را داریم:
X n = { − 1 , 0 , 1 } که احتمال رویدادن هر کدام ۱/۳ است. حال اگر را به صورت زیر تعریف کنیم: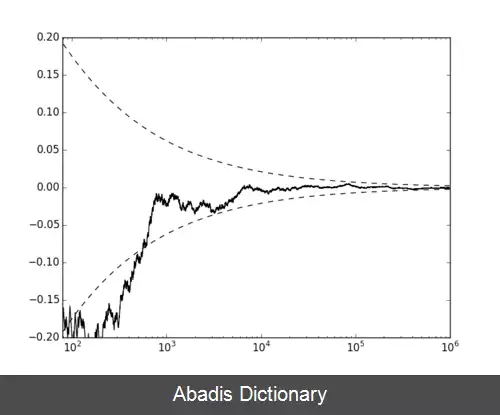
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز قانون Hewitt - Savage 0 - 1 ( به فارسی: هویت سوج ) می دانیم اگر X 1 , X 2 , . . . , X n متغیرهای تصادفی حقیقی با توزیع متقارن حول 0 باشند و S n = ∑ j = 1 n X j باشد، آنگاه داریم: − ∞ = lim inf n → ∞ S n < lim sup n → ∞ S n = ∞ که منظور از lim sup n → ∞ S n و lim inf n → ∞ S n به ترتیب حد سوپریمم و حد اینفیمم است. [ ۴] حال اگر بخواهیم کمی دقیقتر عبارت بالا را توسعه دهیم، باید از قانون Hartman - Wintner ( به فارسی: هارتمن وینتنر ) استفاده کنیم که بیان می کند:
lim inf n → ∞ S n − ϕ ( n ) = lim sup n → ∞ S n ϕ ( n ) = 1 a l m o s t s u r e l y و برای هر S n ای که شرایط زیر را داشته باشد: { E = 0 V a r = σ 2 = f i n i t e داریم:[ ۵]
lim sup n → ∞ S n 2 σ 2 n log log ( n ) = 1 a l m o s t s u r e l y برای درک بهتر مطالب بالا به شکل روبرو توجه کنید. سری را در نظر بگیرید که در آن ، امین رقم اعشاری عدد در سیستم دودویی است. دو نمودار ( نقطه چین ) و ( خط پررنگ ) رسم شده است و به وضوح می توان دید که وقتی n ⟶ ∞ این دو نمودار به هم همگرا می شوند. مثال فرض کنید با دوستتان سنگ، کاغذ، قیچی بازی می کنید به طوری که شما به احتمال ۱/۳ برنده می شوید، به احتمال ۱/۳ بازنده اید و به احتمال ۱/۳ کسی برنده نمی شود. اگر برنده شوید ۱ ریال دریافت می کنید، اگر بازنده شوید ۱ ریال به دوستتان می دهید و اگر کسی برنده نشود هیچ اتفاقی نمی افتد.
متغیر تصادفی X n را مقدار پولی در نظر بگیرید که در مرحله n ام بازی باید بپردازید به این ترتیب برای متغیر تصادفی مقادیر زیر را داریم:
X n = { − 1 , 0 , 1 } که احتمال رویدادن هر کدام ۱/۳ است. حال اگر را به صورت زیر تعریف کنیم:

wiki: قانون لگاریتم های تکراری
