قانون زنجیره ای

قانون زنجیره ای (احتمال). در تئوری احتمال ، قانون زنجیره ای ( به انگلیسی: Chain Rule ) امکان محاسبه توزیع توأم مجموعه ای از متغیرهای تصادفی را تنها با استفاده از احتمالات شرطی می دهد. این قانون در مطالعه شبکه های بیزی مفید است که توزیع احتمال را بر حسب احتمالات شرطی توصیف می کند.
قانون زنجیره ای برای دو پیشامد تصادفی A و B اینطور تعریف می شود:
این قانون در مثال زیر شرح داده شده است.
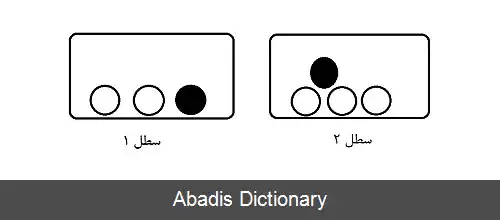
سطل 1 دارای 1 توپ سیاه و 2 توپ سفید و سطل 2 دارای 1 توپ سیاه و 3 توپ سفید می باشد. فرض کنید یک سطل را به طور تصادفی انتخاب کرده و سپس یک توپ از آن سطل بر می داریم. پیشامد A را انتخاب سطل 1 در نظر بگیرید: P ( A ) = P ( A ¯ ) = 1 / 2 . فرض کنید پیشامد B نشان دهنده این باشد که یک توپ سفید برداریم. شانس برداشتن توپ سفید به شرط اینکه اولین سطل را انتخاب کرده باشیم برابر است با P ( B | A ) = 2 / 3 . پیشامد A ∩ B اشتراک دو پیشامد خواهد بود: یعنی انتخاب اولین سطل و یک توپ سفید از آن. احتمال رویداد A ∩ B را می توان با قانون زنجیره ای احتمال پیدا کرد:
برای رویداد های A 1 , … , A n قانون زنجیره به فرمول زیر گسترش می یابد
که می توان با استفاده از استقرا آنرا به شکل زیر نوشت
برای چهار پیشامد ( n = 4 ) قاعده زنجیره ای مطابق زیر است
در کارخانه ای 200 لامپ تولید شده است که 10 تا از این لامپ ها معیوب هستند. 4 لامپ به تصادف از این 200 لامپ انتخاب می کنیم. چقدر احتمال دارد که همه لامپ ها سالم باشند؟ پیشامد ( A i ) برابر با این است که لامپ ( i ) سالم باشد برای ( i = 1 , 2 , 3 , 4 ) ما به دنبال محاسبه احتمال P ( A 1 ∩ A 2 ∩ A 3 ∩ A 4 ) هستیم. توجه کنید:
P ( A 1 ) = 190 200
اگر بدانیم اولین لامپ سالم بوده است، دومین لامپ از میان 189 لامپ سالم و 10 لامپ معیوب انتخاب می شود بنابراین
P ( A 2 ∣ A 1 ) = 189 199
اگر بدانیم اولین و دومین لامپ سالم بوده است، سومین لامپ باید از میان 188 لامپ سالم و 10 لامپ معیوب انتخاب شود بنابراین
P ( A 3 ∣ A 2 ∩ A 1 ) = 188 198
به همین ترتیب برای لامپ چهارم داریم:
P ( A 4 ∣ A 3 ∩ A 2 ∩ A 1 ) = 187 197
بنابراین برای محاسبه مقدار نهایی داریم:
P ( A 1 ∩ A 2 ∩ A 3 ∩ A 4 ) = P ( A 4 ∣ A 3 ∩ A 2 ∩ A 1 ) P ( A 3 ∣ A 2 ∩ A 1 ) P ( A 2 ∣ A 1 ) P ( A 1 ) = 190 200 189 199 188 198 187 197