قانون جابجایی وین ( به انگلیسی: Wien's displacement law ) رابطهٔ بین طول موج بیشینه ( λpeak ) با دمای جسم ( T ) در تابش جسم سیاه را با دمای جسم ( T ) را نشان می دهد. آزمایش ها نشان می دهد که میان طول موج λpeak ( برحسب متر ) و دمای جسم ( T برحسب کلوین ) رابطهٔ زیر برقرار است.
T × λ p e a k = b که در آن T دمای مطلق و b یک ثابت تناسب به نام ثابت جابجایی وین، برابر با ۶۹۹۷۲۸۹۷۷۷۲۱۰۰۰۰۰۰۰♠۲٫۸۹۷۷۷۲۱ ( ۲۶ ) ×۱۰−۳ m K, [ ۱] ، [ ۲] یا b ≈ 2898 μ m . K است.
واژهٔ جابجایی در این قانون بیانگر جابه جا شدن بیشینهٔ تابش با تغییر دمای جسم سیاه است که با افزایش دما، این بیشینه به سمت طول موج های کوچکتر جابه جا می شود. این قانون توسط ویلهلم وین کشف شد.
• با استفاده از قانون جابجایی وین می توان دمای سطح ستاره ها را تخمین زد. با برجسته بودن دو ستاره در صورت فلکی شکارچی، می توان به راحتی تفاوت رنگ بین پای شکارچی آبی - سفید ( T = ۱۲۱۰۰ K ) و بشَن قرمز ( T ≈ ۳۳۰۰ K ) را درک کرد.
• برای مثال دمای بدن انسان ۳۷ درجه است. بیشینهٔ تابش بدن انسان با قراردادن دمای بدن به کلوین در رابطه بالا λ p e a k = 2. 898 × 10 − 3 310 = 9. 34 × 10 − 6 m {\textstyle \lambda _{peak}={\tfrac {2. 898\times 10^{ - 3}}{310}}=9. 34\times 10^{ - 6}m} بنابراین طول موج بیشینه می شود:
λ p e a k = 9. 35 × 10 − 6 m یعنی حدود ۱۰ میکرومتر ( میکرون ) . این طول موج در محدودهٔ فروسرخ قرار دارد که با دوربین فروسرخ و حسگرهای انواعی از مارها قابل آشکارسازی است.
• در مورد خورشید ( دمای ۵۷۷۸ کلوین ) این بیشینه در ناحیه سبز بینایی ( ۵۰۰ نانومتر ) قرار دارد. [ ۳] [ ۴] که با جایگذاری دما λ p e a k × 5778 = 2. 898 × 10 − 3 m . K {\textstyle \lambda _{peak}\times 5778=2. 898\times 10^{ - 3}m. K} خواهد شد: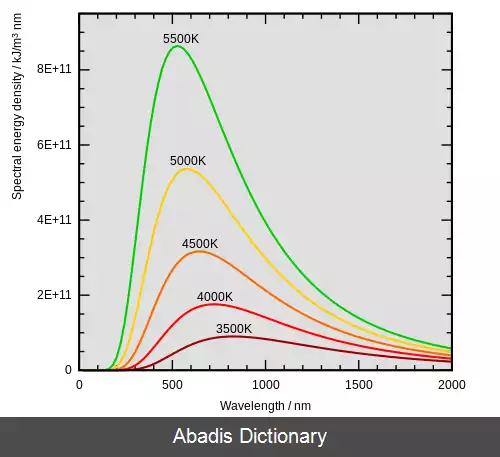
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفT × λ p e a k = b که در آن T دمای مطلق و b یک ثابت تناسب به نام ثابت جابجایی وین، برابر با ۶۹۹۷۲۸۹۷۷۷۲۱۰۰۰۰۰۰۰♠۲٫۸۹۷۷۷۲۱ ( ۲۶ ) ×۱۰−۳ m K, [ ۱] ، [ ۲] یا b ≈ 2898 μ m . K است.
واژهٔ جابجایی در این قانون بیانگر جابه جا شدن بیشینهٔ تابش با تغییر دمای جسم سیاه است که با افزایش دما، این بیشینه به سمت طول موج های کوچکتر جابه جا می شود. این قانون توسط ویلهلم وین کشف شد.
• با استفاده از قانون جابجایی وین می توان دمای سطح ستاره ها را تخمین زد. با برجسته بودن دو ستاره در صورت فلکی شکارچی، می توان به راحتی تفاوت رنگ بین پای شکارچی آبی - سفید ( T = ۱۲۱۰۰ K ) و بشَن قرمز ( T ≈ ۳۳۰۰ K ) را درک کرد.
• برای مثال دمای بدن انسان ۳۷ درجه است. بیشینهٔ تابش بدن انسان با قراردادن دمای بدن به کلوین در رابطه بالا λ p e a k = 2. 898 × 10 − 3 310 = 9. 34 × 10 − 6 m {\textstyle \lambda _{peak}={\tfrac {2. 898\times 10^{ - 3}}{310}}=9. 34\times 10^{ - 6}m} بنابراین طول موج بیشینه می شود:
λ p e a k = 9. 35 × 10 − 6 m یعنی حدود ۱۰ میکرومتر ( میکرون ) . این طول موج در محدودهٔ فروسرخ قرار دارد که با دوربین فروسرخ و حسگرهای انواعی از مارها قابل آشکارسازی است.
• در مورد خورشید ( دمای ۵۷۷۸ کلوین ) این بیشینه در ناحیه سبز بینایی ( ۵۰۰ نانومتر ) قرار دارد. [ ۳] [ ۴] که با جایگذاری دما λ p e a k × 5778 = 2. 898 × 10 − 3 m . K {\textstyle \lambda _{peak}\times 5778=2. 898\times 10^{ - 3}m. K} خواهد شد:

wiki: قانون جابجایی وین
